Краткое описание принципа действия генераторов второй гармоники
ЛАБОРАТОРНАЯ РАБОТА № 3 ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ВНУТРИРЕЗОНАТОРНОЙ ГЕНЕРАЦИИ ВТОРОЙ ГАРМОНИКИ Краткое описание принципа действия генераторов второй гармоники Возможность наблюдения многофотонных процессов, в частности – удвоения частоты, основана на нелинейном взаимодействии интенсивного монохроматического излучения с оптическими диэлектриками без центра инверсии, индуцированная поляризация которых имеет нелинейную зависимость от вызывающего ее электрического поля. При линейном взаимодействии световой волны, распространяющейся в прозрачной среде, под действием световой волны происходит смещение (оптических) электронов в атомах относительно ядер 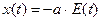 , сопровождающееся появлением дипольного момента , сопровождающееся появлением дипольного момента  , прямо пропорционального напряженности электрического поля возмущающей световой волны , прямо пропорционального напряженности электрического поля возмущающей световой волны  ; здесь ; здесь  , ,  - поляризуемость частицы, - поляризуемость частицы,  - заряд электрона, - заряд электрона,  =2πν - циклическая (круговая) частота возмущающего поля. Поляризация среды =2πν - циклическая (круговая) частота возмущающего поля. Поляризация среды  - это совокупный дипольный момент - это совокупный дипольный момент  атомов, содержащихся в единице объема среды: атомов, содержащихся в единице объема среды:  , (29) , (29)
 - диэлектрическая восприимчивость, - диэлектрическая восприимчивость,  - электрическая проницаемость. - электрическая проницаемость.
Поляризация пропорциональна мгновенному значению индуцирующего ее светового поля  и зависит от дипольного момента и зависит от дипольного момента  и концентрации частиц и концентрации частиц  . При этом колеблющиеся электроны в соответствии с законами электродинамики сами являются (вторичными) источниками излучения, т.е. переизлучают световые колебания с той же частотой. Поляризация на частоте . При этом колеблющиеся электроны в соответствии с законами электродинамики сами являются (вторичными) источниками излучения, т.е. переизлучают световые колебания с той же частотой. Поляризация на частоте  связана с колебаниями электронов на этой частоте: связана с колебаниями электронов на этой частоте:  , (30) , (30)
где  , (31) , (31)
 , ,  - электрическая проницаемость вакуума, - электрическая проницаемость вакуума,  - собственная резонансная частота перехода, - собственная резонансная частота перехода,  - масса электрона, - масса электрона, 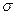 - коэффициент затухания. - коэффициент затухания.
Уменьшение фазовой скорости в среде относительно скорости света в вакууме
(  ) объясняется наличием фазового сдвига (запаздывания) между возбуждающей и переизлученной световыми волнами. Доля энергии световой волны, теряющаяся при ее взаимодействии с частицами среды, определяет потери на поглощение света данной средой. ) объясняется наличием фазового сдвига (запаздывания) между возбуждающей и переизлученной световыми волнами. Доля энергии световой волны, теряющаяся при ее взаимодействии с частицами среды, определяет потери на поглощение света данной средой. При нелинейном взаимодействии отклик оптической среды (без центра инверсии) имеет более сложный вид  , (32) , (32)
где 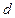 , ,  - нелинейные восприимчивости, определяемые свойствами нелинейной среды и не зависящие от - нелинейные восприимчивости, определяемые свойствами нелинейной среды и не зависящие от  . Коэффициенты . Коэффициенты 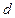 , ,  (и т.д.) представляют собой тензоры, характеризующие нелинейность среды, причем отношение каждого последующего члена к предыдущему имеет значение порядка (и т.д.) представляют собой тензоры, характеризующие нелинейность среды, причем отношение каждого последующего члена к предыдущему имеет значение порядка  . Поэтому для обычных (нелазерных) источников, когда . Поэтому для обычных (нелазерных) источников, когда  , все члены (32), начиная со второго, пренебрежимо малы и нелинейность отклика среды практически отсутствует. , все члены (32), начиная со второго, пренебрежимо малы и нелинейность отклика среды практически отсутствует. Основные достижения нелинейной оптики связаны с использованием нелинейных эффектов, описываемых квадратичной нелинейной восприимчивостью 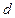 , когда , когда  . В этом случае при гармоническом распределении в нелинейной среде световой волны с частотой . В этом случае при гармоническом распределении в нелинейной среде световой волны с частотой  : :  получим величину получим величину  со следующими составляющими со следующими составляющими  . (33) . (33)
Волна поляризации будет, следовательно, возбуждать в нелинейной среде волну излучения не только с частотой  , но и с частотой , но и с частотой  (называемой второй гармоникой), волновой вектор которой (называемой второй гармоникой), волновой вектор которой  , ,
где 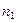 - коэффициент преломления среды для излучения с удвоенной частотой - коэффициент преломления среды для излучения с удвоенной частотой  , ,  - скорость распространения вторичной волны с частотой - скорость распространения вторичной волны с частотой  . . Волновые нелинейные взаимодействия, описываемые квадратичной нелинейной восприимчивостью, принято называть трехфотонными. Для осуществления этих процессов не требуется, чтобы индуцирующее излучение находилось в резонансе с индуцируемым. В нелинейных диэлектрических средах могут генерироваться гармоники света благодаря поглощению двух фотонов и одновременному испусканию фотона суммарной частоты (см. рис. 13).
Следовательно, необходимые условия генерации второй гармоники заключаются в следующем: - в среде должен отсутствовать центр инверсии: потенциальная энергия электрона  и возвращающая сила при и возвращающая сила при  вызывает положительные амплитуды поляризации, например меньшие, чем отрицательные ( вызывает положительные амплитуды поляризации, например меньшие, чем отрицательные (  , рис. 14); , рис. 14); - среда должна быть прозрачна как на основной (возмущающей) частоте, так и на частоте второй гармоники; - ширина запрещенной зоны среды  должна соответствовать выходной энергии вторичного фотона должна соответствовать выходной энергии вторичного фотона  . . Интенсивность излучения второй гармоники  на выходе кристалла длиной на выходе кристалла длиной  пропорциональна пропорциональна 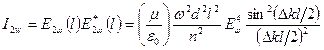 , (34) , (34)
где 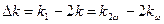 , ,  ; ;  - показатель преломления (такой, что - показатель преломления (такой, что  ) ; ) ;  , ,  - магнитная и электрическая проницаемость среды, соответственно. - магнитная и электрическая проницаемость среды, соответственно. Для входного пучка сечением   . (35) . (35)
Эффективность преобразования поля входного излучения на частоте  в поле на удвоенной частоте в поле на удвоенной частоте 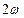  , (36) , (36)
 . .
Эффективность преобразования в приближении плоской возмущающей волны пропорциональна  - интенсивности основного излучения и при - интенсивности основного излучения и при  зависит от интерференции двух волн второй гармоники, описываемой множителем зависит от интерференции двух волн второй гармоники, описываемой множителем  . Длину среды, равную расстоянию между двумя соседними максимами этой интерференционной картины, обычно называют когерентной . Длину среды, равную расстоянию между двумя соседними максимами этой интерференционной картины, обычно называют когерентной
длиной  . Она определяет максимальную длину среды, которую можно использовать для эффективной генерации 2-ой гармоники: . Она определяет максимальную длину среды, которую можно использовать для эффективной генерации 2-ой гармоники: 
Рисунок 13 – Диаграмма энергетических уровней, иллюстрирующая энергетику генерацию второй гармоники 
Рисунок 14 – Соотношения между индуцированной поляризацией  и вызывающим ее синусоидальным электрическим полем и вызывающим ее синусоидальным электрическим полем  в случае линейной (а) и нелинейной среды, не обладающей симметрией инверсии (б) в случае линейной (а) и нелинейной среды, не обладающей симметрией инверсии (б)  . (37) . (37)
При  величина выходного сигнала (6) будет максимальной. В случае нормальной (обычной) дисперсии оптической среды величина рассогласования фаз величина выходного сигнала (6) будет максимальной. В случае нормальной (обычной) дисперсии оптической среды величина рассогласования фаз  между волной поляризации и волной накачки, как правило, велика; следовательно, между волной поляризации и волной накачки, как правило, велика; следовательно,  мала. мала. Если же в нелинейной среде имеет место согласование фаз (  ), то величина выходного сигнала будет значительной и пропорциональной квадрату длины кристалла. ), то величина выходного сигнала будет значительной и пропорциональной квадрату длины кристалла. Поглощенная средой энергия пропорциональна  , (38) , (38)
где  - разность фаз между волной поляризации и возмущающей электромагнитной волной. - разность фаз между волной поляризации и возмущающей электромагнитной волной. При  генерируемая волна отстает по фазе от волны поляризации на генерируемая волна отстает по фазе от волны поляризации на 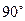 и энергия переходит от волны поляризации к электромагнитной волне ( и энергия переходит от волны поляризации к электромагнитной волне (  ). При ). При  это происходит только при это происходит только при  ; в противном случае происходит обратный процесс передачи энергии, т.е. при несинхронном взаимодействии совершается периодический процесс передачи энергии от падающих волн к генерируемым и обратно. При длине нелинейной среды, равной ; в противном случае происходит обратный процесс передачи энергии, т.е. при несинхронном взаимодействии совершается периодический процесс передачи энергии от падающих волн к генерируемым и обратно. При длине нелинейной среды, равной  , вторая гармоника на выходе отсутствует, а мощность основной волны на выходе равна ее мощности на входе, т.е. потерь энергии не происходит. Для того, чтобы при , вторая гармоника на выходе отсутствует, а мощность основной волны на выходе равна ее мощности на входе, т.е. потерь энергии не происходит. Для того, чтобы при  мощность второй гармоники не уменьшалась, а возрастала, организуют так называемое "квазисинхронное" взаимодействие - скачкообразное изменение фазы в дискретных сечениях среды. мощность второй гармоники не уменьшалась, а возрастала, организуют так называемое "квазисинхронное" взаимодействие - скачкообразное изменение фазы в дискретных сечениях среды. Условие синхронизма Таким образом, эффективность процесса генерации второй гармоники будет зависеть от фазовых соотношений между основной волной и излучением суммарной частоты, т.е. второй гармоникой. Возникает своеобразная интерференция, способная либо усилить, либо ослабить этот процесс. Для обеспечения эффективного процесса генерации излучения с суммарной частотой, т.е. для максимальной перекачки энергии от основной волны ко второй гармонике, необходимо создать такие условия, при которых фазовые скорости распространения волны поляризации  и излучения c суммарной частотой и излучения c суммарной частотой  были бы равны, т.е. волна второй гармоники оставалась бы в фазе с создающей ее волной поляризации. Отсюда вытекает условие эффективной генерации второй гармоники при коллинеарном взаимодействии - так называемое условие фазового синхронизма были бы равны, т.е. волна второй гармоники оставалась бы в фазе с создающей ее волной поляризации. Отсюда вытекает условие эффективной генерации второй гармоники при коллинеарном взаимодействии - так называемое условие фазового синхронизма 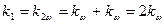 , (39) , (39)
т.к.  , то , то  , или , или 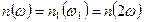 , или , или  . . В обычных средах в оптическом диапазоне всегда существует дисперсия, в силу чего  (обычно показатель преломления в средах с нормальной дисперсией возрастает с увеличением частоты). Поэтому для волн одного и того же типа (обыкновенных или необыкновенных), но с разными частотами, удовлетворить условию фазового синхронизма невозможно. Равенство фазовых скоростей для различных частот создают искусственно, используя свойства волн различной поляризации при их распространении в анизотропной среде. Коэффициент преломления для обыкновенного луча не зависит от направления распространения излучения и для частот (обычно показатель преломления в средах с нормальной дисперсией возрастает с увеличением частоты). Поэтому для волн одного и того же типа (обыкновенных или необыкновенных), но с разными частотами, удовлетворить условию фазового синхронизма невозможно. Равенство фазовых скоростей для различных частот создают искусственно, используя свойства волн различной поляризации при их распространении в анизотропной среде. Коэффициент преломления для обыкновенного луча не зависит от направления распространения излучения и для частот  и и 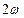 может быть представлен собой окружностями разных радиусов (см. рис. 15). может быть представлен собой окружностями разных радиусов (см. рис. 15). Коэффициент преломления для необыкновенного луча зависит от направления распространения и соответствующие сечения представляют собой эллипсы с разными величинами главных полуосей (для обыкновенного луча - окружности). Из рис. 15 видно, что в анизотропной среде можно найти направление (например, расположенное под углом  к его оптической оси), вдоль которого показатели преломления для обыкновенной волны с частотой к его оптической оси), вдоль которого показатели преломления для обыкновенной волны с частотой  и для необыкновенной волны с частотой и для необыкновенной волны с частотой 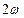 совпадают совпадают  ; ;  , ,
т.е. выполняется условие фазового синхронизма. Тогда  , ,
откуда 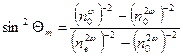 . (40) . (40)
Этот метод, основанный на применении анизотропных кристаллов, обладающих естественным двулучепреломлением, превышающим дисперсию, и является наиболее распространенным методом обеспечения условия фазового синхронизма. 
Рисунок 15 – Нормальные поверхности показателей преломления для обыкновенного и необыкновенного лучей в отрицательном (  ) одноосном кристалле ) одноосном кристалле 
Рисунок 16 – Изменение мощности второй гармоники, получаемой из излучения рубинового лазера, в зависимости от ориентации кристалла KDP (калий дигидрофосфат KH2P2O5) Как было показано выше, для отрицательных двулучепреломляющих кристаллов основная волна должна являться обыкновенным лучом (  -луч), а вторая гармоника - необыкновенным ( -луч), а вторая гармоника - необыкновенным (  -луч). Синхронным является взаимодействие двух (обыкновенной и необыкновенной) основных волн с обыкновенной волной второй гармоники в положительном кристалле и с необыкновенной волной второй гармоники в отрицательном кристалле. Если на входе основные волны имеют одну линейную поляризацию, то синхронизм относится к I типу, разную - то ко II типу. -луч). Синхронным является взаимодействие двух (обыкновенной и необыкновенной) основных волн с обыкновенной волной второй гармоники в положительном кристалле и с необыкновенной волной второй гармоники в отрицательном кристалле. Если на входе основные волны имеют одну линейную поляризацию, то синхронизм относится к I типу, разную - то ко II типу. Фазовый синхронизм возможен и в двухосных кристаллах. Здесь различают также 4 случая взаимодействия (если рассматривать поляризацию двух основных волн на входе и волны второй гармоники на выходе): 1)  ; 2) ; 2) 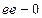 (I тип); (I тип); 3)  ; 4) ; 4)  (II тип). (II тип). Хотя волновые поверхности для обыкновенного и необыкновенного лучей имеют более сложную (чем у одноосных кристаллов) поверхность, направление синхронизма также образует конус вокруг (двух) оптических осей, но уже не обязательно кругового сечения. Особенности ГВГ в направлении синхронизма 3.1. На КПД преобразования оказывает существенное влияние ряд факторов, на некоторых из которых следует остановиться. Прежде всего, это влияние геометрии исходного лазерного пучка, уменьшающее выходную мощность вследствие того, что  (41) (41)
является функцией угла распространения излучения  (по отношению к оптической оси). При отклонении угла (по отношению к оптической оси). При отклонении угла  от угла фазового согласования от угла фазового согласования  мощность второй гармоники быстро убывает: мощность второй гармоники быстро убывает:  , (14) , (14)
где  . . Из рис. 16 видно, условие синхронизма точно выполняется лишь для очень узкого пучка: при отклонении угла распространения  от от  условие синхронизма нарушается и КПД резко падает. условие синхронизма нарушается и КПД резко падает. 3.2. Следует учитывать также тот факт, что изменение температуры анизотропной нелинейной среды, приводящее к угловому сдвигу направления синхронизма, нарушает условие фазового согласования и уменьшает КПД преобразования. 3.3. Для увеличения эффективности преобразования в соответствии с (36) уменьшают сечение пучка, т.е. используют сфокусированные гауссовы пучки, однако только если их конфокальный параметр  , т.е. когда на длине нелинейного кристалла не возникает заметная расходимость пучка, что снижает эффективность преобразования (см. 3.1). , т.е. когда на длине нелинейного кристалла не возникает заметная расходимость пучка, что снижает эффективность преобразования (см. 3.1). 3.4. Т.к. для необыкновенной волны направление луча и направление волновой нормали параллельны только при  и и  , то при синхронном взаимодействии под другими углами необыкновенный световой пучок не будет полностью перекрываться с обыкновенным на всей длине взаимодействия, а различие в направлении волнового и лучевого векторов для необыкновенной волны приведет к сносу энергии необыкновенного пучка относительно энергии обыкновенного; это уменьшит выходную мощность для синхронного взаимодействия I типа и, что более важно, при синхронных взаимодействиях II типа процесс генерации второй частоты может прекратиться вообще. , то при синхронном взаимодействии под другими углами необыкновенный световой пучок не будет полностью перекрываться с обыкновенным на всей длине взаимодействия, а различие в направлении волнового и лучевого векторов для необыкновенной волны приведет к сносу энергии необыкновенного пучка относительно энергии обыкновенного; это уменьшит выходную мощность для синхронного взаимодействия I типа и, что более важно, при синхронных взаимодействиях II типа процесс генерации второй частоты может прекратиться вообще. Если же угол синхронизма  , то снос энергии необыкновенного луча относительно обыкновенного вследствие двулучепреломления отсутствует, допустимый угол расходимости пучка также существенно больше; поэтому 90°-ый синхронизм называют некритичным. , то снос энергии необыкновенного луча относительно обыкновенного вследствие двулучепреломления отсутствует, допустимый угол расходимости пучка также существенно больше; поэтому 90°-ый синхронизм называют некритичным. 3.5. На практике выполнения условия 90°-ного синхронизма добиваются, изменяя температуру нелинейного кристалла и, тем самым, его двулучепреломление - поскольку показатели преломления  и и  по-разному зависят от температуры (обычно по-разному зависят от температуры (обычно  сильнее, чем сильнее, чем  ). На температуру 90°-ного синхронизма оказывает существенное влияние состав кристалла (вплоть до примесей), так что различные образцы одного и того же кристалла (например - ниобата лития LiNbO3) имеют разную температуру синхронизма для одного и того же типа взаимодействия. Поэтому общепринятым способом проверки качества нелинейного кристалла является исследование формы кривой зависимости мощности ГВГ от температуры или угла при проходе последних через значения, соответствующие точному синхронизму. В промышленных образцах ГВТ обычно вводится температурная подстройка синхронизма (см. п. 4). ). На температуру 90°-ного синхронизма оказывает существенное влияние состав кристалла (вплоть до примесей), так что различные образцы одного и того же кристалла (например - ниобата лития LiNbO3) имеют разную температуру синхронизма для одного и того же типа взаимодействия. Поэтому общепринятым способом проверки качества нелинейного кристалла является исследование формы кривой зависимости мощности ГВГ от температуры или угла при проходе последних через значения, соответствующие точному синхронизму. В промышленных образцах ГВТ обычно вводится температурная подстройка синхронизма (см. п. 4). Для кристаллов, в которых для согласования фаз используется температурная подстройка, вводят понятия температурной ширины синхронизма  - температурного интервала, в пределах которого мощность ВГ уменьшается вдвое относительно максимального значения. Теоретическую температурную ширину синхронизма - температурного интервала, в пределах которого мощность ВГ уменьшается вдвое относительно максимального значения. Теоретическую температурную ширину синхронизма  можно вычислить, используя зависимость показателя преломления от температуры: можно вычислить, используя зависимость показателя преломления от температуры:  . (42) . (42)
Аналогичным соотношением связаны экспериментально измеренная температурная ширина синхронизма  и эффективная длина взаимодействия и эффективная длина взаимодействия 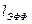 , которая является численной оценкой качества нелинейного кристалла и может быть меньше или равна длине кристалла в направлении распространения взаимодействующих волн. Зная ( , которая является численной оценкой качества нелинейного кристалла и может быть меньше или равна длине кристалла в направлении распространения взаимодействующих волн. Зная (  ), из вышеприведенной зависимости (экспериментально измерив величину температурной ширины синхронизма ), из вышеприведенной зависимости (экспериментально измерив величину температурной ширины синхронизма  ) нетрудно получить значение длины кристалла ) нетрудно получить значение длины кристалла 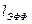 , на которой сохраняется условие согласования фаз: , на которой сохраняется условие согласования фаз:  . (43) . (43)
Если длина кристалла равна 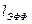 , то кристалл хорошего качества. , то кристалл хорошего качества. Аналогичный анализ можно провести для угловой перестройки, используя для этого угловые, а не температурные производные показателя преломления. 3.6. Существенного увеличения плотности мощности излучения на основной частоте и увеличения КПД преобразования в соответствии с (36) можно достичь, поместив нелинейный оптический кристалл внутрь лазерного резонатора. Если  - коэффициент отражения выходного зеркала лазерного резонатора (обычно - коэффициент отражения выходного зеркала лазерного резонатора (обычно  ), то интенсивность правой волны внутри резонатора значительно (в ), то интенсивность правой волны внутри резонатора значительно (в  раз) больше, чем вне него. Это ведет к существенному увеличению эффективности процесса преобразования основной частоты раз) больше, чем вне него. Это ведет к существенному увеличению эффективности процесса преобразования основной частоты  в частоту ВГ в частоту ВГ 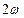 ; при определенных условиях можно почти всю мощность лазера на частоте ; при определенных условиях можно почти всю мощность лазера на частоте  вывести из такого внутрилазерного преобразователя на частоте вывести из такого внутрилазерного преобразователя на частоте  , т.е. получить почти 100%-ную эффективность преобразования. , т.е. получить почти 100%-ную эффективность преобразования. Если при заданной скорости накачки и оптимальном коэффициенте связи резонатора  (обычно это коэффициент пропускания выходного зеркала), использовать выходное зеркало со 100%-ным отражением на основной частоте (обычно это коэффициент пропускания выходного зеркала), использовать выходное зеркало со 100%-ным отражением на основной частоте  и также внутрирезонаторный нелинейный кристалл с и также внутрирезонаторный нелинейный кристалл с  %-ной эффективностью преобразования за 1 проход (причем %-ной эффективностью преобразования за 1 проход (причем  ), то полезные потери собственно лазера остаются оптимальными. Тогда мощность излучения на частоте ), то полезные потери собственно лазера остаются оптимальными. Тогда мощность излучения на частоте 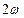 будет равна мощности основного излучения, выводимой ранее на частоте будет равна мощности основного излучения, выводимой ранее на частоте  , т.е. вся мощность собственно лазера может быть преобразована во вторую гармонику (см. рис. 17). В этом случае коэффициент связи будет равен коэффициенту преобразования от , т.е. вся мощность собственно лазера может быть преобразована во вторую гармонику (см. рис. 17). В этом случае коэффициент связи будет равен коэффициенту преобразования от  до до 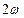 за один проход: за один проход:  , (44) , (44)
где  - мощность бегущей волны внутри резонатора. - мощность бегущей волны внутри резонатора.  , (45) , (45)
 - коэффициент нелинейного преобразования во вторую гармонику. - коэффициент нелинейного преобразования во вторую гармонику.
Максимуму выходной мощности лазера соответствует оптимальный коэффициент связи резонатора лазера  , определяемый диссипативными потерями энергии в резонаторе за цикл , определяемый диссипативными потерями энергии в резонаторе за цикл  и ненасыщенным (начальным) коэффициентом усиления активной среды за цикл и ненасыщенным (начальным) коэффициентом усиления активной среды за цикл  : :  . (46) . (46)
Тогда эффективность преобразования основной частоты во ВГ максимальна при условии  . (47) . (47)
Суммарные потери за проход в этом случае будут определяться как вредными потерями в резонаторе, так и потерями на преобразование частоты:  . (48) . (48)
Если известна общая мощность излучения внутри резонатора  , то часть мощности, которая теряется для резонатора и используется полезно, можно определить, умножив , то часть мощности, которая теряется для резонатора и используется полезно, можно определить, умножив  на на  . В то же время это часть мощности одной бегущей волны . В то же время это часть мощности одной бегущей волны  , преобразованной при одном проходе резонатора, т.е. , преобразованной при одном проходе резонатора, т.е.  . Таким образом, при оптимальной связи . Таким образом, при оптимальной связи  , ,
 . (49) . (49)
Поскольку  , (50) , (50)
где  - интенсивность насыщения лазерного перехода, то - интенсивность насыщения лазерного перехода, то  . (51) . (51)

Рисунок 17 – Схема внутрилазерной генерации второй гармоники: 1 - нелинейный кристалл, 2 - активная среда собственно лазера, 3 - высокоотражающие на частоте лазерной генерации зеркала резонатора 
Рисунок 18 – Температурная зависимость показателей преломления ниобата бария-натрия для длин волн 1064 и 532 нм Используя (17), (20) и (24), можно определить  и и  : :  , (52) , (52)
 . (53) . (53)
Из последнего выражения следует, что  не зависит от начального (ненасыщенного) коэффициента усиления не зависит от начального (ненасыщенного) коэффициента усиления  , т.е. не зависит от накачки - в отличии от обычных лазеров, у которых оптимальное пропускание выходного зеркала (см. (19)) зависит от уровня накачки. Учитывая зависимость , т.е. не зависит от накачки - в отличии от обычных лазеров, у которых оптимальное пропускание выходного зеркала (см. (19)) зависит от уровня накачки. Учитывая зависимость  от от  (18), т.е. фазового рассогласования, которое в свою очередь зависит от направления распространения излучения и температуры, необходимо подчеркнуть, что, меняя ориентацию кристалла или температуру, можно изменять (18), т.е. фазового рассогласования, которое в свою очередь зависит от направления распространения излучения и температуры, необходимо подчеркнуть, что, меняя ориентацию кристалла или температуру, можно изменять  . . Следует иметь в виду также тот факт, что 100%-ное преобразование генерируемого в лазере излучения во вторую гармонику возможно лишь для линейно поляризованного первичного излучения; в случае неполяризованного излучения эффективность преобразования может достигать в лучшем случае 50%, а для однонаправленного преобразования неполяризованного излучения  и то только в случае, если сам нелинейный кристалл не вносит существенных потерь и не приводит к значительному увеличению и то только в случае, если сам нелинейный кристалл не вносит существенных потерь и не приводит к значительному увеличению  лазера, а также не искажает его волновой фронт. Жесткое требование высокого оптического качества нелинейного кристалла обуславливает требование чрезвычайно малых коэффициентов поглощения на частотах основного излучения и второй гармоники, т.к. даже малое поглощение может привести к заметному разогреву кристалла и в результате - к нарушению фазового синхронизма (и, что особенно страшно, к образованию в нелинейном кристалле тепловой линзы). лазера, а также не искажает его волновой фронт. Жесткое требование высокого оптического качества нелинейного кристалла обуславливает требование чрезвычайно малых коэффициентов поглощения на частотах основного излучения и второй гармоники, т.к. даже малое поглощение может привести к заметному разогреву кристалла и в результате - к нарушению фазового синхронизма (и, что особенно страшно, к образованию в нелинейном кристалле тепловой линзы).
| 



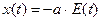 , сопровождающееся появлением дипольного момента
, сопровождающееся появлением дипольного момента  , прямо пропорционального напряженности электрического поля возмущающей световой волны
, прямо пропорционального напряженности электрического поля возмущающей световой волны  ; здесь
; здесь  ,
,  - поляризуемость частицы,
- поляризуемость частицы,  - заряд электрона,
- заряд электрона,  =2πν - циклическая (круговая) частота возмущающего поля. Поляризация среды
=2πν - циклическая (круговая) частота возмущающего поля. Поляризация среды  - это совокупный дипольный момент
- это совокупный дипольный момент  атомов, содержащихся в единице объема среды:
атомов, содержащихся в единице объема среды: , (29)
, (29) - диэлектрическая восприимчивость,
- диэлектрическая восприимчивость,  - электрическая проницаемость.
- электрическая проницаемость. и зависит от дипольного момента
и зависит от дипольного момента  и концентрации частиц
и концентрации частиц  , (30)
, (30) , (31)
, (31) ,
,  - электрическая проницаемость вакуума,
- электрическая проницаемость вакуума,  - собственная резонансная частота перехода,
- собственная резонансная частота перехода,  - масса электрона,
- масса электрона, 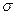 - коэффициент затухания.
- коэффициент затухания. ) объясняется наличием фазового сдвига (запаздывания) между возбуждающей и переизлученной световыми волнами. Доля энергии световой волны, теряющаяся при ее взаимодействии с частицами среды, определяет потери на поглощение света данной средой.
) объясняется наличием фазового сдвига (запаздывания) между возбуждающей и переизлученной световыми волнами. Доля энергии световой волны, теряющаяся при ее взаимодействии с частицами среды, определяет потери на поглощение света данной средой. , (32)
, (32)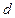 ,
,  - нелинейные восприимчивости, определяемые свойствами нелинейной среды и не зависящие от
- нелинейные восприимчивости, определяемые свойствами нелинейной среды и не зависящие от  . Поэтому для обычных (нелазерных) источников, когда
. Поэтому для обычных (нелазерных) источников, когда  , все члены (32), начиная со второго, пренебрежимо малы и нелинейность отклика среды практически отсутствует.
, все члены (32), начиная со второго, пренебрежимо малы и нелинейность отклика среды практически отсутствует. . В этом случае при гармоническом распределении в нелинейной среде световой волны с частотой
. В этом случае при гармоническом распределении в нелинейной среде световой волны с частотой  получим величину
получим величину  со следующими составляющими
со следующими составляющими . (33)
. (33) (называемой второй гармоникой), волновой вектор которой
(называемой второй гармоникой), волновой вектор которой ,
,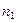 - коэффициент преломления среды для излучения с удвоенной частотой
- коэффициент преломления среды для излучения с удвоенной частотой  - скорость распространения вторичной волны с частотой
- скорость распространения вторичной волны с частотой  и возвращающая сила при
и возвращающая сила при  вызывает положительные амплитуды поляризации, например меньшие, чем отрицательные (
вызывает положительные амплитуды поляризации, например меньшие, чем отрицательные (  , рис. 14);
, рис. 14); должна соответствовать выходной энергии вторичного фотона
должна соответствовать выходной энергии вторичного фотона  .
. на выходе кристалла длиной
на выходе кристалла длиной  пропорциональна
пропорциональна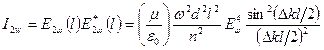 , (34)
, (34)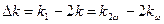 ,
,  ;
;  - показатель преломления (такой, что
- показатель преломления (такой, что  ) ;
) ;  ,
, 
 . (35)
. (35)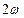
 , (36)
, (36) .
. - интенсивности основного излучения и при
- интенсивности основного излучения и при  зависит от интерференции двух волн второй гармоники, описываемой множителем
зависит от интерференции двух волн второй гармоники, описываемой множителем  . Длину среды, равную расстоянию между двумя соседними максимами этой интерференционной картины, обычно называют когерентной
. Длину среды, равную расстоянию между двумя соседними максимами этой интерференционной картины, обычно называют когерентной . Она определяет максимальную длину среды, которую можно использовать для эффективной генерации 2-ой гармоники:
. Она определяет максимальную длину среды, которую можно использовать для эффективной генерации 2-ой гармоники:

 и вызывающим ее синусоидальным электрическим полем
и вызывающим ее синусоидальным электрическим полем  в случае линейной (а) и нелинейной среды, не обладающей симметрией инверсии (б)
в случае линейной (а) и нелинейной среды, не обладающей симметрией инверсии (б) . (37)
. (37) величина выходного сигнала (6) будет максимальной. В случае нормальной (обычной) дисперсии оптической среды величина рассогласования фаз
величина выходного сигнала (6) будет максимальной. В случае нормальной (обычной) дисперсии оптической среды величина рассогласования фаз  между волной поляризации и волной накачки, как правило, велика; следовательно,
между волной поляризации и волной накачки, как правило, велика; следовательно,  ), то величина выходного сигнала будет значительной и пропорциональной квадрату длины кристалла.
), то величина выходного сигнала будет значительной и пропорциональной квадрату длины кристалла. , (38)
, (38) - разность фаз между волной поляризации и возмущающей электромагнитной волной.
- разность фаз между волной поляризации и возмущающей электромагнитной волной. и энергия переходит от волны поляризации к электромагнитной волне (
и энергия переходит от волны поляризации к электромагнитной волне (  ). При
). При  ; в противном случае происходит обратный процесс передачи энергии, т.е. при несинхронном взаимодействии совершается периодический процесс передачи энергии от падающих волн к генерируемым и обратно. При длине нелинейной среды, равной
; в противном случае происходит обратный процесс передачи энергии, т.е. при несинхронном взаимодействии совершается периодический процесс передачи энергии от падающих волн к генерируемым и обратно. При длине нелинейной среды, равной  , вторая гармоника на выходе отсутствует, а мощность основной волны на выходе равна ее мощности на входе, т.е. потерь энергии не происходит. Для того, чтобы при
, вторая гармоника на выходе отсутствует, а мощность основной волны на выходе равна ее мощности на входе, т.е. потерь энергии не происходит. Для того, чтобы при  мощность второй гармоники не уменьшалась, а возрастала, организуют так называемое "квазисинхронное" взаимодействие - скачкообразное изменение фазы в дискретных сечениях среды.
мощность второй гармоники не уменьшалась, а возрастала, организуют так называемое "квазисинхронное" взаимодействие - скачкообразное изменение фазы в дискретных сечениях среды. и излучения c суммарной частотой
и излучения c суммарной частотой 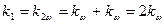 , (39)
, (39) , то
, то  , или
, или 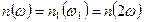 , или
, или  .
. (обычно показатель преломления в средах с нормальной дисперсией возрастает с увеличением частоты). Поэтому для волн одного и того же типа (обыкновенных или необыкновенных), но с разными частотами, удовлетворить условию фазового синхронизма невозможно. Равенство фазовых скоростей для различных частот создают искусственно, используя свойства волн различной поляризации при их распространении в анизотропной среде. Коэффициент преломления для обыкновенного луча не зависит от направления распространения излучения и для частот
(обычно показатель преломления в средах с нормальной дисперсией возрастает с увеличением частоты). Поэтому для волн одного и того же типа (обыкновенных или необыкновенных), но с разными частотами, удовлетворить условию фазового синхронизма невозможно. Равенство фазовых скоростей для различных частот создают искусственно, используя свойства волн различной поляризации при их распространении в анизотропной среде. Коэффициент преломления для обыкновенного луча не зависит от направления распространения излучения и для частот  к его оптической оси), вдоль которого показатели преломления для обыкновенной волны с частотой
к его оптической оси), вдоль которого показатели преломления для обыкновенной волны с частотой  ;
;  ,
, ,
,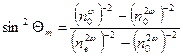 . (40)
. (40)
 ) одноосном кристалле
) одноосном кристалле
 -луч), а вторая гармоника - необыкновенным (
-луч), а вторая гармоника - необыкновенным (  ; 2)
; 2) 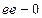 (I тип);
(I тип); ; 4)
; 4)  (II тип).
(II тип). (41)
(41) , (14)
, (14) .
. , т.е. когда на длине нелинейного кристалла не возникает заметная расходимость пучка, что снижает эффективность преобразования (см. 3.1).
, т.е. когда на длине нелинейного кристалла не возникает заметная расходимость пучка, что снижает эффективность преобразования (см. 3.1). и
и  , то при синхронном взаимодействии под другими углами необыкновенный световой пучок не будет полностью перекрываться с обыкновенным на всей длине взаимодействия, а различие в направлении волнового и лучевого векторов для необыкновенной волны приведет к сносу энергии необыкновенного пучка относительно энергии обыкновенного; это уменьшит выходную мощность для синхронного взаимодействия I типа и, что более важно, при синхронных взаимодействиях II типа процесс генерации второй частоты может прекратиться вообще.
, то при синхронном взаимодействии под другими углами необыкновенный световой пучок не будет полностью перекрываться с обыкновенным на всей длине взаимодействия, а различие в направлении волнового и лучевого векторов для необыкновенной волны приведет к сносу энергии необыкновенного пучка относительно энергии обыкновенного; это уменьшит выходную мощность для синхронного взаимодействия I типа и, что более важно, при синхронных взаимодействиях II типа процесс генерации второй частоты может прекратиться вообще. , то снос энергии необыкновенного луча относительно обыкновенного вследствие двулучепреломления отсутствует, допустимый угол расходимости пучка также существенно больше; поэтому 90°-ый синхронизм называют некритичным.
, то снос энергии необыкновенного луча относительно обыкновенного вследствие двулучепреломления отсутствует, допустимый угол расходимости пучка также существенно больше; поэтому 90°-ый синхронизм называют некритичным. и
и  по-разному зависят от температуры (обычно
по-разному зависят от температуры (обычно  - температурного интервала, в пределах которого мощность ВГ уменьшается вдвое относительно максимального значения. Теоретическую температурную ширину синхронизма
- температурного интервала, в пределах которого мощность ВГ уменьшается вдвое относительно максимального значения. Теоретическую температурную ширину синхронизма  . (42)
. (42) и эффективная длина взаимодействия
и эффективная длина взаимодействия 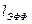 , которая является численной оценкой качества нелинейного кристалла и может быть меньше или равна длине кристалла в направлении распространения взаимодействующих волн. Зная (
, которая является численной оценкой качества нелинейного кристалла и может быть меньше или равна длине кристалла в направлении распространения взаимодействующих волн. Зная (  ), из вышеприведенной зависимости (экспериментально измерив величину температурной ширины синхронизма
), из вышеприведенной зависимости (экспериментально измерив величину температурной ширины синхронизма  . (43)
. (43) - коэффициент отражения выходного зеркала лазерного резонатора (обычно
- коэффициент отражения выходного зеркала лазерного резонатора (обычно  ), то интенсивность правой волны внутри резонатора значительно (в
), то интенсивность правой волны внутри резонатора значительно (в  раз) больше, чем вне него. Это ведет к существенному увеличению эффективности процесса преобразования основной частоты
раз) больше, чем вне него. Это ведет к существенному увеличению эффективности процесса преобразования основной частоты  (обычно это коэффициент пропускания выходного зеркала), использовать выходное зеркало со 100%-ным отражением на основной частоте
(обычно это коэффициент пропускания выходного зеркала), использовать выходное зеркало со 100%-ным отражением на основной частоте  ), то полезные потери собственно лазера остаются оптимальными. Тогда мощность излучения на частоте
), то полезные потери собственно лазера остаются оптимальными. Тогда мощность излучения на частоте  , (44)
, (44) - мощность бегущей волны внутри резонатора.
- мощность бегущей волны внутри резонатора. , (45)
, (45) - коэффициент нелинейного преобразования во вторую гармонику.
- коэффициент нелинейного преобразования во вторую гармонику. и ненасыщенным (начальным) коэффициентом усиления активной среды за цикл
и ненасыщенным (начальным) коэффициентом усиления активной среды за цикл  :
: . (46)
. (46) . (47)
. (47) . (48)
. (48) , то часть мощности, которая теряется для резонатора и используется полезно, можно определить, умножив
, то часть мощности, которая теряется для резонатора и используется полезно, можно определить, умножив  . В то же время это часть мощности одной бегущей волны
. В то же время это часть мощности одной бегущей волны  . Таким образом, при оптимальной связи
. Таким образом, при оптимальной связи ,
, . (49)
. (49) , (50)
, (50) - интенсивность насыщения лазерного перехода, то
- интенсивность насыщения лазерного перехода, то . (51)
. (51)

 и
и  :
: , (52)
, (52) . (53)
. (53) , т.е. не зависит от накачки - в отличии от обычных лазеров, у которых оптимальное пропускание выходного зеркала (см. (19)) зависит от уровня накачки. Учитывая зависимость
, т.е. не зависит от накачки - в отличии от обычных лазеров, у которых оптимальное пропускание выходного зеркала (см. (19)) зависит от уровня накачки. Учитывая зависимость  (18), т.е. фазового рассогласования, которое в свою очередь зависит от направления распространения излучения и температуры, необходимо подчеркнуть, что, меняя ориентацию кристалла или температуру, можно изменять
(18), т.е. фазового рассогласования, которое в свою очередь зависит от направления распространения излучения и температуры, необходимо подчеркнуть, что, меняя ориентацию кристалла или температуру, можно изменять  и то только в случае, если сам нелинейный кристалл не вносит существенных потерь и не приводит к значительному увеличению
и то только в случае, если сам нелинейный кристалл не вносит существенных потерь и не приводит к значительному увеличению