 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ПРОВЕДЕНИЕ ИЗМЕРЕНИЙ И ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА 12
ФГБОУ ВПО «КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» КАФЕДРА ФИЗИКИ ЛАБОРАТОРНАЯ РАБОТА № 314 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВНУТРЕНЕГО ТРЕНИЯ, ДЛИНЫ СВОБОДНОГО ПРОБЕГА И ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА Методическое указание к выполнению лабораторной работы по разделу «Молекулярная физика» для студентов всех форм обучения по всем специальностям
Калининград Цель работы: определить коэффициент внутреннего трения воздуха, рассчитать длину свободного пробега и эффективный диаметр молекул воздуха.
Реквизит:ручной секундомер, барометр.
ВВЕДЕНИЕ Рассмотрим течение газа или жидкости по цилиндрической трубе радиуса R и длиной l. Давления P1 и Р2, поддерживаемые на концах трубы, различны; газ течёт по трубе под влиянием перепада давлений ΔР = Р2 - P1. Скорость U течения газа направлена везде вдоль оси трубы, а по величине меняется в перпендикулярном к оси направлении в зависимости от одной координаты - расстояния r от оси. Мы можем поэтому написать для потока импульса, переносимого в радиальном направлении:
Рассмотрим объём жидкости, ограниченный проведённой внутри трубки и коаксиальной с ней цилиндрической поверхностью некоторого радиуса r (рис.1). Для определения силы трения, действующей на рассматриваемый объём газа со стороны остального газа, необходимо поток импульса через поверхность трубки умножить на площадь этой поверхности, равную 2πrl:
Рис.1.
Сила трения компенсируется силой перепада давлений, приложенных к основаниям цилиндра, которая равна
откуда после интегрирования получаем: Произвольная постоянная определяется из условия равенства нулю скорости на самой поверхности трубы, то есть при r = R1. Окончательно получаем:
Таким образом, текущий в трубе газ имеет параболический профиль скоростей (рис.2): скорость меняется по квадратичному закону от нуля на стенке до максимального значения Определим
где
Отсюда
Полный объём газа V, протекающий за время Δt, определяется формулой Пуазейля:
Из уравнения (9) следует, что Рис.2.
Величины правой части (10) доступны измерению, поэтому этим уравнением можно воспользоваться для экспериментального определения коэффициента вязкости газа. Кинетическая теория газов устанавливает связь между коэффициентом внутреннего трения идеального газа η, средней длиной свободного пробега молекул газа
где ρ - плотность газа. Более точный вывод соотношения (11), учитывающий распределение скоростей молекул по закону Максвелла, даёт другое выражение коэффициента внутреннего трения. Так, для воздуха
Заменим в этом уравнении
где T - абсолютная температура, R - универсальная газовая постоянная, μ - молярная масса газа. Справочные данные:
Р - атмосферное давление. Из соотношения
можно рассчитать эффективный диаметр молекул воздуха. Здесь т - число молекул в единице объёма, σ - их эффективный диаметр. Концентрация n определяется из формулы:
где Р – давление воздуха, равное атмосферному, к – постоянная Больцмана, равная 1,38∙10-23 Дж/К.
МЕТОДИКА ИЗМЕРЕНИЯ
Рис.3.
Для эксперимента используется установка, изображённая на рис.3. Расход газа через капилляр (5) равен расходу жидкости из сосуда (1). При истечении жидкости из сосуда давление в нём установится меньше атмосферного, за счёт этой разности давлений воздух снаружи протекает через капилляр в сосуд. Разность давлений - атмосферного Р и давления в сосуде Ро - регистрируется с помощью гидроманометра (3). В виду того, что в процессе эксперимента скорость истечения жидкости при понижении её уровня уменьшается, необходимо учесть изменение перепада давлений в процессе эксперимента. Для этого рассчитываем средний перепад давлений, который определяется как полусумма перепадов давлений в начале и в конце эксперимента.
где ρ - плотность воды, h – расстояние между уровнями жидкости гидроманометра (см. рис.4).
Тогда рабочая формула примет вид:
Схема гидроманометра.
В начале эксперимента
Рис. 4.
ПРОВЕДЕНИЕ ИЗМЕРЕНИЙ И ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА 3.1. Открыть кран 8 на трубке 6 для соединения сосуда с атмосферой при заполнении сосуда водой. 3.2. Для заполнения сосуда водой открыть кран 7 на трубке 9 и присоединить его к водопроводному крану. Осторожно открыть водопроводный кран. 3.3. Заполнить сосуд до уровня с отметкой "0", закрыть краны – водопроводный, 7 и 8, отсоединить шланг от водопроводного крана. 3.4. Поместить шланг с краном 7 в водопроводную раковину и открыть кран. Выждать, чтобы процесс течения установился. Об этом судят по показаниям гидроманометра. 3.5. В момент прохождения уровня у отметки 2 шкалы 4 запустить секундомер, одновременно снять показания n1 и n2 гидроманометра. 3.6. Выждать, когда вытечет 10 литров воды, на делении 12 остановить секундомер и одновременно снять показания гидроманометра n3 и n4. 3.7. Данные занести в таблицу эксперимента. Таблица
Здесь: Р - атмосферное давление по барометру; t - температура окружающего воздуха по Цельсию; Δt - время истечения жидкости; h1, h2 - расстояния между уровнями жидкости гидроманометра в начале и в конце эксперимента; V – объём жидкости, вытекающей из сосуда за время Δt; n1, n2 - показания гидроманометра в начале и n3, n4 - в конце эксперимента; η - коэффициент внутреннего трения воздуха. 3.8. По результатам эксперимента определить значение коэффициента внутреннего трения (вязкости) воздуха по формуле (18), табличное значение 0,0182 мПа∙с. 3.9. Определить среднюю длину свободного пробега молекул воздуха по формуле (23), табличное значение 10-7 м. 3.10. Рассчитать эффективный диаметр молекул воздуха по формулам (24) и (25), табличное значение 3·10-10 м. 3.11. Определить погрешность измерения коэффициента вязкости как ошибку косвенного измерения, учитывая только ошибки округления, ошибкой измерения времени пренебречь. Интервалами округления h считать: для V - 0,25 литра, для n – 2 мм. При расчёте погрешностей руководствоваться методическими указаниями №100. Справочные данные:
КОНТРОЛЬНЫЕ ВОПРОСЫ (ПРИМЕРНЫЕ) 4.1. Сущность явления внутреннего трения в газах и в жидкостях. 4.2. Напишите формулу Пуазейля и объясните, при каких условиях она справедлива. 4.3. Что такое длина свободного пробега молекул газа? Как её рассчитать, используя данные эксперимента? 4.4. Что такое эффективный диаметр молекул? 4.5. В чём сущность метода измерения коэффициента внутреннего трения газа в данной работе? 4.6. В каких единицах измеряется коэффициент внутреннего трения газа? 4.7. Какие явления переноса существуют и каким законам подчиняются?
ЛИТЕРАТУРА 5.1. И.В.Савельев, Курс общей физики, т.1, Москва, «Наука», 1977г., с.395. 5.2. А. А. Детлаф, Б.М.Яворский, Я.Б. Милковская, Курс физики, т.1. 5.3. Физический практикум под редакцией В. И. Ивероновой.
ПРИЛОЖЕНИЕ
12 |



 (1)
(1) (2)
(2)
 . Приравнивая эти силы, получим уравнение:
. Приравнивая эти силы, получим уравнение: , (3)
, (3)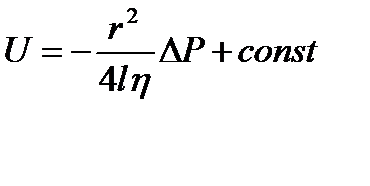 (4)
(4)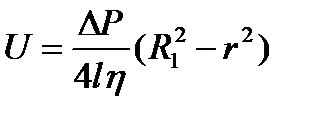 (5)
(5) на оси трубки.
на оси трубки. объём газа, вытекающего в единицу времени через цилиндр радиуса r. Очевидно, что дифференциал этой функции
объём газа, вытекающего в единицу времени через цилиндр радиуса r. Очевидно, что дифференциал этой функции , (6)
, (6) - скорость газа на расстоянии r от оси, а
- скорость газа на расстоянии r от оси, а  - площадь кольца радиуса r и ширины dr.
- площадь кольца радиуса r и ширины dr. Поскольку
Поскольку  , то
, то  (7)
(7) (8)
(8) (9)
(9)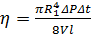 (10)
(10) и средней арифметической скоростью
и средней арифметической скоростью  их движения в виде:
их движения в виде: , (11)
, (11) (12)
(12) и ρ с помощью известных из кинетической теории газов соотношений и, проведя элементарные преобразования, получим:
и ρ с помощью известных из кинетической теории газов соотношений и, проведя элементарные преобразования, получим: , (13)
, (13)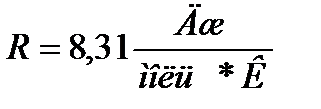

 (14)
(14) , (15)
, (15)

 , (16)
, (16) ,
,
 (17)
(17) (18)
(18) :
: 
 В конце эксперимента:
В конце эксперимента: 
 - плотность воды;
- плотность воды;  - длина капилляра;
- длина капилляра;  - радиус капилляра.
- радиус капилляра.