 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Критерии воспроизводимости 12
Отклонение от среднего di: di = |Xi – Xср.| 1. di = |1,5 - 1,8| = 0,3 2. di = |1,6 - 1,8| = 0,2 3. di = |1,6 - 1,8| = 0,2 4. di = |1,7 - 1,8| = 0,1 5. di = |1,8 - 1,8| = 0 6. di = |1,8 - 1,8| = 0 7. di = |2,0 - 1,8| = 0,2 8. di = |2,1 - 1,8| = 0,3 9. di = |2,1 - 1,8| = 0,3 Среднее отклонение dср.: dср. = Размах варьирования (диапазон выборки) ω: ω = Хmax. – Xmin = 2,1 – 1,5 = 0,6. Дисперсия S2: S2 = Если известно истинное значение (μ), то дисперсия рассчитывается по формуле: V = S2 = Cтандартное отклонение выборки (абсолютное) S: S = √ S2 = Если известно истинное значение (μ), то стандартное отклонение генеральной совокупности рассчитывается по формуле: σ = S = Приближенно стандартное отклонение можно оценить по размаху варьирования: S = Стандартное отклонение среднего SХср.: SХср. = Относительное стандартное отклонение Sr: Sr = 3. Оценка правильности (оценка систематических отклонений) Доверительный интервал δ или Σα: δ ( Σα или ∆Хср.) = ± 0,90: = ±1,86*0,2 / 3 = 0,124 0,95: = ±2,31*0,2 / 3 = 0,154 0,99: = ±3,36*0,2 / 3 = 0,224 где tP или tα,k – коэффициент Стьюдента, приводимый в таблицах для различных доверительных вероятностей (Р или α) и различных степеней свободы k или ƒ (см. табл. 4). Доверительная вероятность (Р или α) показывает, сколько вариант из 100 попадает в данный интервал. Действительное - а или истинное значение - μ: а = μ = Хср. ± δ = 1,8 ± 0,17 . Относительная погрешность среднего результата Е: Е,% = Таблица 4 Коэффициенты Стьюдента (tP или tα,k)
Таким образом, доверительный интервал характеризует как воспроизводимость результатов химического анализа, так и – если известно истинное значение Хист. или μ – их правильность. Заполните таблицу 5. Таблица 5
Сравнение выборок Чтобы решить вопрос, принадлежат ли разные выборки одной совокупности, можно воспользоваться статистическими методами проверки гипотез, в частности нуль-гипотезы. 1. Если известны дисперсии или стандартные отклонения разных выборок, можно сравнить их и решить вопрос о принадлежности этих выборок одной совокупности по воспроизводимости. При этом целесообразно использовать статистический критерий F-распределения (F- критерий Фишера): Fp = Нуль-гипотеза строится на предположении о неразличимости дисперсий или стандартных отклонений. F-критерий рассчитывают по экспериментальным данным. Найденные значения Fp сравнивают с табличным значением Fт (см. табл. 6). Если Fp < Fт, нуль-гипотеза подтверждается, выборки обладают одинаковой точностью, систематические погрешности отсутствуют, их можно отнести к одной совокупности. ЕслиFp > Fт, нуль-гипотеза отвергается, воспроизводимости двух методов разные, присутствуют систематические погрешности, поэтому выборки нельзя отнести к одной совокупности (объединить). Таблица 6 Теоретические значения критерия Фишера (FТ)
Установив однородность дисперсий выборок и отсутствие систематических погрешностей, можно решать вопросы о принадлежности единичных результатов выборок к одной совокупности и о правильности того или иного метода определения. 2. Если известны средние значения выборок с однородной дисперсией, можно судить о принадлежности всех результатов одной выборке. Сравнение средних позволяет выявить случайные погрешности. Нуль-гипотеза здесь строится на предположении об идентичности а1 и а2, то есть незначимости различия Х1,ср. и Х2,ср. При этом целесообразно использовать статистический критерий Стьюдента (t-критерий). T-критерий рассчитывают по экспериментальным данным по формуле: tp = где Sср.2 = Найденное значение tp сравнивают с табличным значением tт (см. табл. 2). Если tp < tт, нуль-гипотеза подтверждается, расхождение между средними значениями незначимо, случайные погрешности отсутствуют и выборки можно отнести к одной генеральной совокупности, следовательно данные обеих серий можно объединить. Еслиtp > tт, нуль-гипотеза отвергается, расхождение между средними значениями значимо, поэтому выборки не принадлежат одной и той же генеральной совокупности.
ВЫВОД:
12 |



 = 1,6 / 9 = 0,18.
= 1,6 / 9 = 0,18. , где (n – 1) это число степеней свободы k или ƒ, тогда S2 =
, где (n – 1) это число степеней свободы k или ƒ, тогда S2 =  = 2,56 / 8 = 0,32.
= 2,56 / 8 = 0,32. .
. = 0,57.
= 0,57. .
. = 0,6 / 3 = 0,2.
= 0,6 / 3 = 0,2. = 0,07.
= 0,07. = 11,1 %.
= 11,1 %. ,
, = 0,17*100 / 1,8 = 9,4 %.
= 0,17*100 / 1,8 = 9,4 %.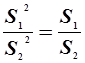 ,где S12 > S22, S1 > S2.
,где S12 > S22, S1 > S2. ,
, .
.