 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Вероятностная нейронная сеть.
Вероятностная нейронная сеть применяется для решения задач классификации. В отличие от задач кластеризации, где классы, на которые необходимо разбить множество данных, не заданы, в задаче классификации указано количество классов, к которому может быть отнесен каждый пример, и задано обучающее множество – для каждого обучающего набора определён класс, к которому он относится. Вероятностная сеть для каждого входного вектора определяет вероятности, с которыми этот вектор принадлежит каждому классу. Вероятностная сеть имеет три слоя: входной, радиальный и выходной. Радиальный нейрон – это нейрон, функцией активации которого является Гауссиан, соответствующий выражению для плотности вероятности при нормальном распределении:
Выражение записано для j-того нейрона. Здесь mi – n-мерный центр функции (аналог математического ожидания), а
Рис. 9.5. Двумерная функция Гаусса Входной слой, как в многослойном персептроне, имеет столько нейронов, сколько параметров имеют входные вектора. Радиальные нейроны включаются в сеть по мере обучения по одному на каждый пример. Каждый из них имеет гауссовскую функцию с центром в этом примере. Таким образом, в вероятностной нейронной сети столько нейронов в промежуточном радиальном слое, сколько примеров существует в обучающем множестве. Каждый нейрон входного слоя соединен со всеми нейронами радиального слоя. Для каждого радиального нейрона синаптические веса связей, соединяющих с ним входные нейроны, устанавливаются равными элементам соответствующего вектора-образца. Например: пусть j-тый представленный сети для обучения вектор-пример имеет вид:
Рис. 9.6. Добавление нейрона в радиальный слой Значения весов принимаются равными элементам обучающего примера, то есть:
Выходные элементы добавляются по мере обучения сети по одному для каждого заданного класса примеров. Выходной элемент соединен лишь с радиальными элементами, относящихся к его классу, и суммирует выходы всех радиальных элементов, принадлежащих к его классу. Полученная сумма никак не обрабатывается, поэтому значения выходных сигналов получаются пропорциональны оценкам вероятности принадлежности вектора к соответствующему классу. Например, пусть добавленный ранее j-тый обучающий пример относится к классу А. Если до этого класс А уже встречался в обучающем множестве, то новый радиальный нейрон просто соединяется с ним единичной связью, и его выход будет суммироваться с другими входящими сигналами.
Рис. 9.7. Присоединение радиального нейрона к существующему выходному. Если же класс А встречается впервые, то в сеть будет добавлен новый выходной нейрон, и породивший его радиальный нейрон соединится с ним.
Рис.9.8. Добавление выходного нейрона Иногда дополнительно добавляют еще один нейрон, который будет вычислять максимум от поданых на него сигналов от выходного слоя. Тогда именно этот единственный нейрон и будет образовывать искусственный выходной слой, а нейроны выходного слоя будут называться нейронами слоя суммирования. Выходной максимизирующий нейрон будет однозначно указывать класс, к которому принадлежит входной вектор. Общий такой вид построенной и одновременно обученной вероятностной нейронной сети отображен на РИС,
Рис. 9.9. Пример архитектуры сети PNN с нейроном типа MAX. Преимущества. Обучение вероятностной нейронной сети намного проще, чем ВackРropagation. Недостатком сети является ее размер, поскольку она фактически содержит в себе все обучающие данные, требует много памяти и может медленно работать. После того как сеть построена, неизвестный экземпляр можно подать на вход сети, и в результате прямого прохода через сеть выходной слой укажет класс, к которому, вероятнее всего, принадлежит образец.
|



 (9.14)
(9.14) - разброс (аналог дисперсии). Для двумерного входного вектора (x1,x2) радиальная функция активации имеет вид:
- разброс (аналог дисперсии). Для двумерного входного вектора (x1,x2) радиальная функция активации имеет вид:
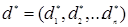 . Тогда в сеть будет добавлен один нейрон радиального слоя:
. Тогда в сеть будет добавлен один нейрон радиального слоя:
 ,
,  …
…  . Функция активации принимает вид:
. Функция активации принимает вид: (9.15)
(9.15)

