 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Алгоритм функционирования сети Кохонена
1. Инициализация сети. Весовым коэффициентам сети даются небольшие случайные значения. Общее число синоптических весов - M*N (см. Рис. ). Начальная зона соседства показана на Рис. . 2. Предъявление сети нового входного сигнала. 3. Вычисление расстояния до всех нейронов сети: Расстояния dj от входного сигнала до каждого нейрона j определяются по формуле:
где xi - i-ый элемент входного сигнала в момент времени t, wij(t) - вес связи от i-го элемента входного сигнала к нейрону j в момент времени t. 4. Выбор нейрона с наименьшим расстоянием: выбирается нейрон-победитель j*, для которого расстояние dj самое малое. 5. Настраивание весов нейрона j* и его соседей: Делается настраивание весов для нейрона j* и всех нейронов из его окрестности NE. Новые значения весов: wij(t+1)=wij(t)+η(t)(xi(t)-wij(t)) (9.4) где η(t) - скорость обучения, которая уменьшается с течением времени (положительное число, меньше единицы). 6. Возвращение к шагу 2. В алгоритме используется коэффициент скорости обучения, который постепенно уменьшается, для тонкой коррекции на новой эпохе. В результате центр устанавливается в определенной позиции, которая удовлетворительным образом кластеризует примеры, для которых данный нейрон является победителем. После того, как сеть научена распознаванию структуры данных, ее можно использовать как средство визуализации при анализе данных. Области применения. Кластерный анализ, распознавание образов, классификация.
Сеть Хопфилда Сеть Хопфилда использует три слоя: входной, слой Хопфилда и выходной слой. Каждый слой имеет одинаковое количество нейронов. Входы слоя Хопфилда подсоединены к выходам соответствующих нейронов входного слоя через изменяющиеся веса соединений. Выходы слоя Хопфилда подсоединяются ко входам всех нейронов слоя Хопфилда, за исключением самого себя, а также к соответствующим элементам в выходном слое. В режиме функционирования, сеть направляет данные из входного слоя через фиксированные веса соединений к слою Хопфилда. Слой Хопфилда колеблется, пока не будет завершено определенное количество циклов, и текущее состояние слоя передается на выходной слой. Это состояние отвечает образу, уже запрограммированному в сеть. Структурная схема сети Хопфилда приведена на рис. 9.3.
Рис. 9.3. Структурная схема сети Хопфилда Задача, решаемая данной сетью, как правило, формулируется так. Известен некоторый образцовый набор двоичных сигналов (изображений, звуковых оцифровок, других данных, которые описывают определенные объекты или характеристики процессов). Сеть должна уметь с зашумленного сигнала, представленного на ее вход, выделить ("припомнить" по частичной информации) соответствующий образец или "дать вывод" о том, что входные данные не отвечают ни одному из образцов. Сеть Хопфилда представляет собой ассоциативную память. «Ассоциативная память» означает, что по вектору, поданному на вход, сетью будет создан на выходе один из запомненных ранее эталонных векторов, наиболее "похожий" (в некотором выбранном смысле) на данный входной вектор. Пусть компоненты эталонных векторов могут принимать только значения +1 и -1. Ответ сети Хопфидла для i-того нейрона для каждого следующего (t+1) цикла может быть представлен выражением:
где f - передаточная функция в виде пороговой, приведена на рис. 9.4.
Рис. 9.4. Передаточные функции
Если функция f -жесткая пороговая функция, ее также обозначают как sgn(x) – «сигнатура», взятие знака выражения. При этом в самом начале (t=0) выход нейрона совпадает со входом:
Рассмотрим процесс обучения сети, т.е. процесс определения весов
Тогда веса
Действительно, с учетом того, что
Пусть теперь задано М эталонных векторов {хk} = x1, x2,...xk, подлежащих запоминанию в нейросети. Тогда веса
Окончательно запишем формулу для определения весов:
Основной особенностью сети Хопфилда является то, что обучение, т.е. вычисление весов wij, проводится однократно еще до функционирования сети по заданному набору эталонных образов. Именно этой матрицей весовых коэффициентов набор эталонов и запоминается в сети. Алгоритм функционирования сети 1. На стадии инициализации сети синаптические коэффициенты устанавливаются таким образом:
Здесь i и j - индексы, соответственно, предсинаптического и постсинаптического нейронов; xik, xjk - i-ый и j-ый элементы вектора k-ого образца. 2. На входы сети подается неизвестный сигнал. Его распространение непосредственно устанавливает значения выходов: yi(0) = xi , i = 1...n, поэтому обозначения на схеме сети входных сигналов в явном виде носит чисто условный характер. Ноль в скобке yi означает нулевую итерацию в цикле работы сети. 3. Рассчитывается новое состояние нейронов
и новые значения выходов
4. Проверяем, изменились ли выходные значения выходов за последнюю итерацию. Если да - переход к пункту 2, иначе (если выходы стабилизировались) - конец. При этом выходной вектор представляет собой образец, что лучше всего отвечает входным данным. Иногда сеть не может провести распознавания и выдает на выходе несуществующий образ. Такой образ часто называют «химерой». Это связано с проблемой ограниченности возможностей сети. Для сети Хопфилда число запомненных образов m не должно превышать величины, приблизительно равной 0.15*n (15% от размерности векторов). |



 (9.3)
(9.3)
 (9.5)
(9.5)
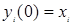 (9.6)
(9.6) . Пусть сети необходимо запомнить только один эталонный образ:
. Пусть сети необходимо запомнить только один эталонный образ:  . Очевидно, если направить его на вход сети, ответ сети должен быть равен этому же образу:
. Очевидно, если направить его на вход сети, ответ сети должен быть равен этому же образу: (9.7)
(9.7) (9.8)
(9.8) , в этом случае имеем:
, в этом случае имеем:
 (9.9)
(9.9) (9.10)
(9.10) (9.11)
(9.11) (9.12)
(9.12)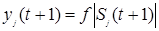 (9.13)
(9.13)