 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Относительная объемная деформация
где V – первоначальный объем образца; DV – изменение объема образца, которое определяется с помощью волюметра. В пределах линейной зависимости между общими деформациями (продольными или объемными) и приращением осевого давления Ds1 находим модуль общей линейной деформации
Модуль объемной деформации:
Между модулем объемной и модулем линейной деформации существует взаимосвязь:
откуда коэффициент относительной поперечной деформации аналогичен коэффициенту Пуассона:
2.6.3. Лопастные испытания на сдвиг при кручении Для определения сопротивления сдвигу водонасыщенных слабых грунтов обычно используют крыльчатку. Этот метод был впервые применен в Швеции. При лопастных испытаниях в забой скважины ниже конца обсадной трубы в грунт вдавливается лопастная крыльчатка (рис.2.27). После чего вращением рукоятки с помощью двойного червячного редуктора производится полный поворот ее на 360о и грунт срезается по цилиндрической поверхности высотой h и диаметром d. Замеряется максимальный скручивающий момент Mкр .
Рис.2.27. Схема четырехлопастной крыльчатки Сопротивление сдвигу определяется по формуле
Метод лопастных испытаний широко применяется при определении общего предельного сопротивления сдвигу слабых илистых и глинистых грунтов и соответствует недренированному их состоянию. При расчетах принимают ts»c, т.е. сопротивление сдвигу равно силам сцепления. 2.6.4. Испытания по методу шарового штампа (метод Н.А.Цытовича) Этот метод используется для определения сил сцепления и длительной прочности слабых илистых, глинистых, лессовых, вечномерзлых льдистых грунтов в полевых и лабораторных условиях при помощи шаровой пробы. Условия испытания. Дают одну ступень нагрузки с таким расчетом, чтобы отношение осадки к диаметру шарового штампа было больше 1/200. Тогда упругими деформациями грунта можно пренебречь. Из теоретических соображений отношение осадки штампа S к его диаметру D должно быть менее 0,1, то есть
Рис.2.28. Установка для полевых испытаний связных грунтов методом шарового штампа: 1 – часть сферы диаметром 30-50 см; 2 – шток с грузовой площадкой; 3 – штатив; 4 – индикатор часового типа Нормативные и расчетные деформационные и прочностные Характеристики грунтов
Грунты в основании фундаментов, как правило, неоднородные. Поэтому определение какой-либо его характеристики по исследованию одного образца дает только частное значение. Для определения нормативных характеристик грунта проводят серию определений каждого показателя. Нормативные значения физических свойств и модуля деформации грунтов определяются как среднеарифметические величины из общего числа определений:
где n – число экспериментов по определению характеристики, xi – частное значение искомой характеристики. Характеристики x, используемые в расчетах, называют расчетными и определяют по формуле
где gq – коэффициент надежности. Расчетные значения физических характеристик грунта, кроме плотности грунта r, определяются при gq = 1. Нормативные значения прочностных характеристик – угла внутреннего трения jn и сцепления cn – определяются не непосредственно из опытов, а после построения графиков сопротивления грунта сдвигу. Поскольку построение графиков сопротивления сдвигу по точкам вносит в расчеты элемент субъективности, результаты серии опытов на сдвиг аппроксимируют прямой с использованием для обработки экспериментальных данных метода наименьших квадратов. При этом число определений сопротивлений сдвигу при одном уровне нормальных напряжений s должно быть не менее шести. Нормативное значение прямой cn и jn находим по формулам
где n – число экспериментов по определению сопротивления грунта сдвигу ti при напряжении si;
Расчетные значения прочностных характеристик cn,jn, плотность грунта r, удельный вес, которые используются для определения устойчивости массивов грунта, определяются по формуле (2.50). При этом коэффициент надежности по грунту gq находят из выражения
где rт – параметр точности оценки среднего значения характеристики грунта. Знак перед показателем rт выбирают такой, который обеспечивает большую надежность расчета. Для сил сцепления c и tgj величину rт определяют по формуле rт = tan, (2.55) для плотности грунта, удельного веса
где ta – коэффициент, зависящий от односторонней доверительной вероятности a, принимаемый по таблицам; n – коэффициент вариации определяемой характеристики. Коэффициент вариации
где s – среднее квадратичное отклонение определяемой характеристики; xn – нормативное значение характеристики. Среднее квадратичное отклонение для c и tgj вычисляют по формулам
где Среднее квадратичное отклонение для плотности r и удельного веса g определяют по формуле
где xn – нормативное значение характеристики; xi – частное значение характеристики при i-м определении. Пользуясь этими формулами, при числе экспериментов не менее 6 определяют расчетные характеристики грунта. Доверительная вероятность a расчетных значений характеристик грунтов принимается при расчетах оснований по несущей способности, равной 0,95, и по деформациям, равным 0,85. Для грунтов оснований опор мостов и труб под насыпями при расчете оснований по несущей способности a = 0,98, по деформациям a = 0,90. Расчетные значения характеристик грунтов c, j и r для расчетов по несущей способности обозначают cI, jI, rI, а по деформациям – cII, jII, rII. Для предварительных расчетов нормативные и расчетные значения прочностных и деформационных характеристик можно брать из таблиц СНиПа (табл. I.1, I.2 приложения I). В этом случае принимаются следующие значения коэффициентов надежности по грунту: в расчетах оснований по деформациям gq =1,0; в расчетах оснований по несущей способности: для удельного сцепления gq(c)=1,5, для угла внутреннего трения песчаных грунтов gq(j)=1,1, для пылевато-глинистых грунтов gq(rт)=1,15. |



 ,
, . (2.44)
. (2.44) .
. , (2.45)
, (2.45) . (2.46)
. (2.46)
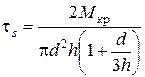 . (2.47)
. (2.47) 0,1. В этом случае при испытаниях штампами различного диаметра результаты будут практически одинаковыми. По результатам испытаний определяют сцепление грунта по формуле
0,1. В этом случае при испытаниях штампами различного диаметра результаты будут практически одинаковыми. По результатам испытаний определяют сцепление грунта по формуле . (2.48)
. (2.48)
 , (2.49)
, (2.49) , (2.50)
, (2.50) , (2.51)
, (2.51) , (2.52)
, (2.52) . (2.53)
. (2.53) , (2.54)
, (2.54) , (2.56)
, (2.56) , (2.57)
, (2.57) , (2.58)
, (2.58) , (2.59)
, (2.59) , а D определяется по формуле (2.53).
, а D определяется по формуле (2.53). , (2.60)
, (2.60)