 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Сопротивление грунтов сдвигу при трехосном сжатии
Существуют способы определения показателей сопротивления грунтов сдвигу, основанные на раздавливании образцов грунта в приборе трехосного сжатия – стабилометре, в условиях всестороннего давления. В этом случае сдвиг грунта происходит не по заранее фиксированным плоскостям, как в срезном приборе, а по площадкам, на которых действуют касательные напряжения, способные преодолеть сопротивление грунта сдвигу. Горизонтальное давление на образец грунта s2 создается жидкостью, заполняющей прибор, а вертикальное s1 – внешней нагрузкой от штампа прибора. Постепенно доводя грунт до разрушения, находят показатели, характеризующие предельное состояние грунта. При этом горизонтальные и вертикальные напряжения представляют собой главные напряжения, зная величину которых, можно найти касательные напряжения, вызвавшие сдвиг грунта по площадкам, расположенным под углом 45о - Испытание грунтов на трехосное сжатие производят по стандартной методике (см.рис.2.11): цилиндрический образец грунта 1, заключенный в резиновую оболочку 2, предварительно подвергают всестороннему давлению, равному s2 = s3, затем, после загасания деформации от всестороннего давления, прикладывают осевую нагрузку Р увеличивающимися ступенями до разрушения образца или потери им устойчивости. По результатам испытаний можно определить значения эффективных напряжений в момент разрушения образца
Зная главные напряжения в момент разрушения образца, строят круги напряжений Мора (рис.2.26).
Рис.2.26. Круги Мора, построенные по результатам испытаний образцов грунта на сжатие в стабилометре: а – сыпучие грунты; б – связные грунты
Величина сдвигающих напряжений не может быть больше предельного значения, определяемого по уравнениям (2.39) или (2.40) и соответствующего возникновению беспрерывного скольжения (сдвига) одной части грунта по другой:
Эти значения напряжений на предельной прямой отвечают некоторой экспериментальной точке М, которая одновременно должна принадлежать и кругу предельных напряжений Мора. Это возможно лишь в том случае, когда прямая ОМ (см.рис.2.26,а) или О1М (см.рис.2.26,б) будет касательной к кругу напряжений, то есть составит с радиусом круга в точке касания угол в 90о и пройдет через начало координат O или О/. Зная величины главных напряжений s1 и s2 и учитывая, что на кривой сдвига треугольники ОМС или О/МC прямоугольные, получим для сыпучих грунтов
а учитывая, что
получим
Для связных грунтов
или
Уравнения (2.42) и (2.43) представляют собой математическое выражение условия предельного равновесия (условие прочности Мора) соответственно сыпучих и связных грунтов. Эти уравнения широко используются при определении предельной нагрузки на грунт, в расчетах устойчивости массивов грунта и в расчетах давления грунта на ограждения. Кроме того, по данным испытаний в стабилометре определяют значение относительной продольной деформации
где Si – осадка для любой ступени нагрузки; h – первоначальная высота образца грунта. |



 к главному напряжению.
к главному напряжению. (2.41)
(2.41)
 ,
, .
. ,
, и
и  ,
, . (2.42)
. (2.42)

 . (2.43)
. (2.43)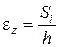 ,
,