 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Условный экстремум функций нескольких переменных. 12
Собственно это та же задача отыскания наибольших и наименьших значений функции, но для функций, у которых переменные связаны между собой некоторыми добавочными условиями. Этой задаче можно дать и геометрическую интерпретацию. Пусть на плоскости XOY задана функция z=f(x,y) и линия L: j(x,y)=0. Требуется на линии L найти такую точку P(x,y), в которой значение функции z=f(x,y) было бы наибольшим или наименьшим по сравнению со значениями этой функции в точках линии L, находящихся вблизи точки P(x,y). Такие точки P называются точками условного экстремума функции z=f(x,y) на линии L. В отличие от обычной точки экстремума, значение функции в точке условного экстремума сравнивается со значениями не во всех точках некоторой ее окрестности, а только в тех, которые лежат на линии L. Точка обычного экстремума (или безусловного) является и точкой условного экстремума для любой линии, проходящей через эту точку. Обратное неверно. Рассмотрим этот вопрос нахождения условного экстремума на примере функции двух переменных, если эти переменные связаны одним условием. Пусть требуется найти максимумы и минимумы функции
при условии, что x и y связаны уравнением
При наличии условия (6) из двух переменных x и y независимым будет только одна, например х, так как y определяется из равенства (6) как функция от х. Если бы мы разрешили уравнение (6) относительно у, то, подставляя в равенство (5) вместо у найденное выражение, получили бы функцию одного переменного х и свели бы задачу к задаче об исследовании на максимум и минимум функции одного независимого переменного х. Но можно решить задачу, не разрешая уравнения (6) относительно x и y. При тех значениях х, при которых функция u может иметь максимум или минимум, производная от u по х должна обращаться в нуль. Из (5) находим
Следовательно, в точках экстремума
Из равенства (6) находим:
Это равенство удовлетворяется для всех x и y, удовлетворяющих уравнению (6). Умножив члены равенства (8) на неопределенный пока коэффициент
или
Последнее равенство выполняется во всех точках экстремума. Подберем
Тогда при этих значениях x и y из равенства (9) следует равенство
Таким образом, получается, что в точках экстремума удовлетворяются три уравнения:
с тремя переменными x,y и
12 |



 (5)
(5)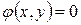 (6)
(6)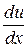 , помня, что у есть функция от х:
, помня, что у есть функция от х: .
. . (7)
. (7) . (8)
. (8) и сложив их соответствующими членами равенств (7), получим:
и сложив их соответствующими членами равенств (7), получим:
 . (9)
. (9) .
.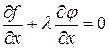 .
. (10)
(10) по переменным x,y и
по переменным x,y и