 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Определение наибольшего и наименьшего значений функции двух переменных в замкнутой области. 12
Лекция 28. Исследование на экстремум функций нескольких переменных. Условный экстремум функций нескольких переменных.
Определим более точно, что такое точки экстремума для функции двух переменных. Определение. Функция Максимумы и минимумы функции называются экстремумами, а Пусть M0(x0; y0)– точка какого-либо экстремума (точка максимума или точка минимума) функции Теорема 1. Если в точке экстремума M0(x0; y0) существуют частные производные
Доказательство. 1) Рассмотрим функцию
2) Рассмотрим теперь функцию
Теорема доказана. Заметим, что условия (1) являются лишь необходимыми условиями экстремума в точке M0(x0; y0) дифференцируемой в этой точке функции Теорема 2.(Достаточные условия экстремума ) Пусть M0(x0; y0) – такая точка из области D определения функции
Тогда: 1) Если 2) Если 3) Если 4) Если Пример 1. Пусть х и у – количества двух произведенных товаров; p1 = 8 руб. и p2 = 10 руб. – цена единицы каждого из этих товаров соответственно; C = 0,01(x2+ xy+ y2) – функция затрат (в рублях) на производство этих товаров. Тогда доход R от продажи товаров составит R = 8x+10y (руб.), а прибыль П составит (в рублях) П = R – C = 8x + 10y – 0,01(x2+xy+y2). Найдем объемы х и у товаров, при которых прибыль П будет максимальной. 1) Сначала найдем значения (х;у), подозрительные на экстремум для функции П:
2) Теперь исследуем найденную подозрительную на экстремум для функции П точку М0(200; 400). Для этого найдем в этой точке значения
и это верно для любых (х; у), а значит, и в точке М0(200; 400), то
Так как Пример 2. Найти точки экстремума и экстремальные значения функции Решение. Данная функция
Сначала найдем точки плоскости хоу, подозрительные на экстремум для данной функции
Затем, найдя частные производные второго порядка от функции
Вычисляя теперь числовые значения этих величин для каждой из четырех подозрительных на экстремум точек, получим следующие выводы об этих точках:
Теперь найдем два экстремальных (максимальных) значения функции
Определение наибольшего и наименьшего значений функции двух переменных в замкнутой области.
Рассмотрим следующую задачу. Пусть
Вернемся к рис. 2. Поставим следующий вопрос: в каких точках области Очевидно, что искомые точки области Из сказанного выше вытекает следующая схема нахождения этих точек, аналогичная той, что была изложена для функций одной переменной. 1. Находим все подозрительные на экстремум точки функции 2. Находим все подозрительные на экстремум точки функции 3. Не исследуя найденные в пунктах 1 и 2 подозрительные точки (это излишне), находим значения функции
Решение. Выполним изложенную выше схему. 1. Найдем внутри треугольника (в области D) точки, подозрительные на экстремум для нашей функции z. Для этого сначала найдем частные производные первого порядка
Эти производные существуют (их можно вычислить) для любых (х; у). Следовательно, точками, подозрительными на экстремум, будут лишь те, для которых обе эти частные производные равны нулю:
Точка 2. Найдем теперь точки, подозрительные на экстремум, на границе треугольника. а) Исследуем сначала участок ОА границы (у = 0; 0 £ х £ 1). На этом участке б) Исследуем теперь участок ОВ границы треугольника ( там х = 0; 0 £ у £ 1). На этом участке функция в) Наконец, исследуем участок АВ границы. Так как на AB (убедитесь в этом) у = - х + 1 (0 £ х £ 1), то там функция z принимает вид: Итак, полный набор подозрительных на экстремум точек функции
3. А теперь найдем значения функции z во всех найденных подозрительных точках и выберем из этих значений наибольшее значение zнаиб и наименьшее значение zнаим:
Таким образом, zнаиб = 3 и достигается функцией z в треугольнике ОАВ сразу в двух точках – в его вершинах А и В. А Пример 4. Городской бюджет имеет возможность потратить на социальное жилье не более 600 млн. рублей, располагая при этом проектами и участками земли под 10 пятиэтажных домов на 90 квартир каждый и под 8 девятиэтажных домов на 120 квартир каждый. Средняя сметная стоимость одной квартиры в пятиэтажном доме составляет 400 тысяч рублей, а в девятиэтажном 500 тысяч рублей. Сколько пятиэтажных и сколько девятиэтажных домов должен построить город, чтобы получить максимальное число квартир? Решение. Пусть х – искомое количество пятиэтажных домов, у – девятиэтажных, а z – общее количество квартир в этих домах: z = 90x + 120y Стоимость всех квартир в пятиэтажных домах составит 90 × 0,4·х = 36х млн. рублей, а в девятиэтажных 120 × 0,5·у = 60у млн. рублей. Согласно условиям задачи имеем: 0 £ х £10; 0 £ у £ 8; 36х + 60у £ 600
Реализуем изложенную выше схему решения такого рода задач. 1. Найдем внутри пятиугольника точки, подозрительные на экстремум для функции z. Так как 2. Найдем точки, подозрительные на экстремум, на границах пятиугольника. На каждом из пяти отрезков, составляющих границу пятиугольника, функция z – линейная функция вида z = ax + by, а следовательно, своих наибольшего и наименьшего значений она достигает на границах отрезков. То есть искомое наибольшее значение zнаиб функция z достигает в одной из угловых точек (О; А; М1; М2; В). Вычисляя значение z в этих точках, получим: z(О) = 0; z(A) = 960; z(M1) = 1260; z(M2) = 1380; z(B) = 900. Таким образом zнаимб = 1380 и достигается оно в точке M2(10; 4). То есть наибольшее число квартир (1380) получится, если будут построены 10 пятиэтажных домов и 4 девятиэтажных. Пример 5. Доказать, что из всех треугольников, имеющих данный периметр 2р, наибольшую площадь имеет равносторонний треугольник. Решение.Обозначим стороны треугольника через х, у и z. По формуле Герона площадь треугольника S= Вместо того, чтобы искать экстремум этой функции, будем искать экстремум ее квадрата f(x,y) = S2 = p(p - x)(p - y)( x + y - p); ∂f/∂x = p(p - y)(2p - 2x - y); ∂f/∂y = p(p - x)(2p - 2y - x). Решаем систему уравнений Эта система приводит к таким четырем системам:
1) 3)
находим стационарные точки: (p,p); (2p/3, 2p/3); (p,0); (0,p). Исследованию подлежит только одна точка М(2p/3, 2p/3), т.к. остальные точки не удовлетворяют смыслу задачи: не может быть треугольника, у которого сторона равна половине периметра. Исследуем на экстремум точку М(2p/3, 2p/3): ∂2f/∂x2 = -2p(p-y); ∂2f/∂x∂y = p(2x+2y-3p); ∂2f/∂y2 = -2p(p-x);
D=AC-B2= D>0, а т.к. А<0, то в исследуемой точке функция достигает максимума. Итак, в единственной стационарной точке функция достигает максимума, а потому и наибольшего значения; таким образом, при х=2p/3, y=2p/3 функция достигает и наибольшего значения. Но тогда z=2p-x-y=2p/3. А т.к. х=у=z, то треугольник – равносторонний.
12 |



 Исследование функций многих переменных на экстремум – процедура гораздо более сложная, чем аналогичная процедура для функций одной переменной. Поэтому ограничимся рассмотрением этого вопроса на наиболее простом и наглядном примере функции двух переменных
Исследование функций многих переменных на экстремум – процедура гораздо более сложная, чем аналогичная процедура для функций одной переменной. Поэтому ограничимся рассмотрением этого вопроса на наиболее простом и наглядном примере функции двух переменных  ( см рис.1). Здесь M1(x1; y1), M2(x2; y2), M3(x3; y3)– точки экстремума этой функции. А именно, точки М1 и М3 – точки минимума функции, а точка М2 – точка ее максимума. На рис.1 представлена функция с тремя точками экстремума, но этих точек, естественно, может быть и больше, и меньше.
( см рис.1). Здесь M1(x1; y1), M2(x2; y2), M3(x3; y3)– точки экстремума этой функции. А именно, точки М1 и М3 – точки минимума функции, а точка М2 – точка ее максимума. На рис.1 представлена функция с тремя точками экстремума, но этих точек, естественно, может быть и больше, и меньше. имеет максимум ( минимум ) в точке
имеет максимум ( минимум ) в точке  , если для любой точки
, если для любой точки  , находящейся в некоторой окрестности
, находящейся в некоторой окрестности  - окрестности точки
- окрестности точки  (
(  ).
).  , где
, где  . Тогда справедлива
. Тогда справедлива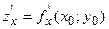 и
и  , то обе они равны нулю:
, то обе они равны нулю:
 . Так как
. Так как  – экстремальное значение этой функции, то производная
– экстремальное значение этой функции, то производная 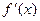 этой функции при х = х0, если она существует, равна нулю:
этой функции при х = х0, если она существует, равна нулю:
 . Так как
. Так как  – экстремальное значение этой функции, то производная
– экстремальное значение этой функции, то производная  этой функции при y = y0, если она существует, равна нулю:
этой функции при y = y0, если она существует, равна нулю:

 >0 и
>0 и  >0 ( или С>0 при А=0 ), то M0(x0; y0) – точка минимума функции
>0 ( или С>0 при А=0 ), то M0(x0; y0) – точка минимума функции 
 , определяемые выражениями (4). Так как
, определяемые выражениями (4). Так как ,
,
 а
а  то точка М0(200; 400) – точка максимума функции П. То есть прибыль П от продаж будет максимальной при х = 200 (ед) и у = 400 (ед) и равна 2800 руб.
то точка М0(200; 400) – точка максимума функции П. То есть прибыль П от продаж будет максимальной при х = 200 (ед) и у = 400 (ед) и равна 2800 руб.
 – функция двух переменных, определенная для любых х и у, то есть на всей плоскости хоу, и имеющая в каждой ее точке частные производные первого порядка:
– функция двух переменных, определенная для любых х и у, то есть на всей плоскости хоу, и имеющая в каждой ее точке частные производные первого порядка:
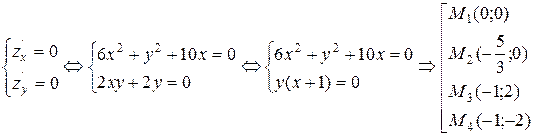
 :
:
 - точка min.
- точка min. - точка max.
- точка max. - не точка экстремума.
- не точка экстремума. - не точка экстремума.
- не точка экстремума.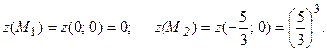
 , где
, где  – внутренняя часть области
– внутренняя часть области 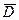 , а Г – ее граница (рис. 8.6).
, а Г – ее граница (рис. 8.6).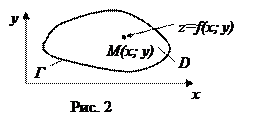 То, что функция
То, что функция  . То есть понятие непрерывности функции двух переменных аналогично понятию непрерывности функции одной переменной. Как и функции одной переменной, функции двух переменных, образованные из элементарных функций, непрерывны для всех значений своих аргументов, для которых они определены. Это касается и функций трех, четырех и более переменных.
. То есть понятие непрерывности функции двух переменных аналогично понятию непрерывности функции одной переменной. Как и функции одной переменной, функции двух переменных, образованные из элементарных функций, непрерывны для всех значений своих аргументов, для которых они определены. Это касается и функций трех, четырех и более переменных. , рассматриваемой на замкнутом отрезке [a; b] оси ох.
, рассматриваемой на замкнутом отрезке [a; b] оси ох. и
и  равны нулю (или одна равна нулю, а другая не существует; или обе не существуют).
равны нулю (или одна равна нулю, а другая не существует; или обе не существуют). Пример 3. Найти zнаиб и zнаим функции
Пример 3. Найти zнаиб и zнаим функции  , рассматриваемой в замкнутой области
, рассматриваемой в замкнутой области  и
и  :
:

 , очевидно, принадлежит области D (рассматриваемому треугольнику). То есть она – подозрительная на экстремум точка для заданной функции z внутри треугольника, причем она там единственная.
, очевидно, принадлежит области D (рассматриваемому треугольнику). То есть она – подозрительная на экстремум точка для заданной функции z внутри треугольника, причем она там единственная. – функция одной переменной х. Ее производная
– функция одной переменной х. Ее производная  существует для всех x Î [0; 1]. Поэтому свои экстремальные значения функция z может иметь или в точке, где
существует для всех x Î [0; 1]. Поэтому свои экстремальные значения функция z может иметь или в точке, где  , то есть в точке
, то есть в точке  , или на концах отрезка ОА, то есть в точках О(0; 0) и А(1; 0).
, или на концах отрезка ОА, то есть в точках О(0; 0) и А(1; 0). (0 £ у £ 1) – функция одной переменной у. Повторяя рассуждения пункта (а), приходим к выводу, что свои экстремальные значения функция z может иметь или в точке
(0 £ у £ 1) – функция одной переменной у. Повторяя рассуждения пункта (а), приходим к выводу, что свои экстремальные значения функция z может иметь или в точке  , или на концах отрезка ОВ, то есть в точках О(0; 0) и B(0; 1).
, или на концах отрезка ОВ, то есть в точках О(0; 0) и B(0; 1). (0 £ х £ 1). Ее производная
(0 £ х £ 1). Ее производная 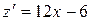 , поэтому своих экстремальных значений функция z может достигать лишь в точке, где
, поэтому своих экстремальных значений функция z может достигать лишь в точке, где  , то есть в точке
, то есть в точке  , либо на концах отрезка АВ, то есть в точках А и В.
, либо на концах отрезка АВ, то есть в точках А и В. в треугольнике ОАВ таков:
в треугольнике ОАВ таков: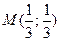 ;
;  ;
; 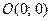 ;
;  ;
;  .
.
 и достигается функцией z в треугольнике ОАВ в его внутренней точке
и достигается функцией z в треугольнике ОАВ в его внутренней точке  .
. Данные ограничительные неравенства выполняются, очевидно, в пятиугольнике
Данные ограничительные неравенства выполняются, очевидно, в пятиугольнике  (рис.4). В этой замкнутой области
(рис.4). В этой замкнутой области  , и эти частные производные заведомо не равны нулю, то подозрительных на экстремум точек внутри пятиугольника нет.
, и эти частные производные заведомо не равны нулю, то подозрительных на экстремум точек внутри пятиугольника нет.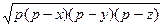 . Замечая, что z = 2p –x - y, мы получим S как функцию только двух независимых переменных: S=
. Замечая, что z = 2p –x - y, мы получим S как функцию только двух независимых переменных: S=  .
.
 2)
2) 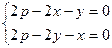
 4)
4) 


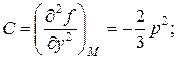
 ;
;