 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Полный дифференциал функции многих переменных. 12
Для начала рассмотрим это понятие на примере функции двух переменных
Если
Приближенные равенства (10) будут тем точнее, чем меньше
А теперь будем считать
При бесконечно малых приращениях аргументов
При
Или короче:
Выражения (14) и (15) представляют собой так называемый полный дифференциал функции Аналогично, если
Или короче:
А конечное приращение
Эта формула тем точнее, чем меньше Полные дифференциалы функций многих переменных являются аналогами полного дифференциала функции одной переменной
Полные дифференциалы функций многих переменных – это абстрактные понятия. Они, как и дифференциал функции одной переменной, имеют в основном теоретическое значение. А вот приближенные формулы (11), (18) и им подобные, определяющие конечное приращение функции при конечных приращениях ее аргументов, широко применяются и на практике. Пример 10. При измерении размеров цилиндра (его радиуса основания Решение. Объем цилиндра
Ошибки
Упражнения 1. Найти частные производные первого порядка функции Ответ: 2. Найти частные производные функции Ответ: 3. Найти приближенное приращение Ответ:
4. При измерении на местности треугольника получены следующие данные: сторона а = 100м ± 2м; сторона b = 200м ± 3м; угол между ними a = 60° ± 1°. С какой степенью точности (с какой максимальной погрешностью) будет вычислена сторона с ? Ответ: максимальная погрешность для с составит ±4,35м. 12 |



 . Для этого рассмотрим приращение
. Для этого рассмотрим приращение 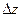 функции
функции  при условии, что аргументы х и у получат некоторые приращения
при условии, что аргументы х и у получат некоторые приращения  и
и  :
:
 (9)
(9)
 (11)
(11) и
и 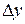 не просто малыми, а бесконечно малыми. В этом случае обозначим их символами dx и dy соответственно и будем называть дифференциалами аргументов х и у:
не просто малыми, а бесконечно малыми. В этом случае обозначим их символами dx и dy соответственно и будем называть дифференциалами аргументов х и у: – это бесконечно малое
– это бесконечно малое  – это бесконечно малое
– это бесконечно малое  и
и  и приращение функции
и приращение функции  будет, согласно (11), бесконечно малым. Обозначим его символом
будет, согласно (11), бесконечно малым. Обозначим его символом  и будем называть дифференциалом функции
и будем называть дифференциалом функции  приближенное равенство (11) станет уже точным:
приближенное равенство (11) станет уже точным:

 в точке
в точке  .
. – функция трех переменных, то ее полный дифференциал
– функция трех переменных, то ее полный дифференциал  в точке
в точке  найдется по формуле:
найдется по формуле:

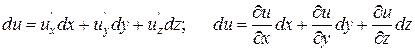
 такой функции, соответствующее конечным приращениям
такой функции, соответствующее конечным приращениям 
 , который определяется равенством:
, который определяется равенством:
 и его высоты
и его высоты  ) из-за несовершенства измерительных приборов возможно допущение малых ошибок
) из-за несовершенства измерительных приборов возможно допущение малых ошибок  и
и  соответственно. Найти максимально возможные абсолютную и относительную ошибки при вычислении объема
соответственно. Найти максимально возможные абсолютную и относительную ошибки при вычислении объема  цилиндра.
цилиндра. – функция двух переменных
– функция двух переменных  при вычислении объема цилиндра
при вычислении объема цилиндра 

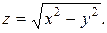

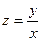 первого и второго порядков.
первого и второго порядков.
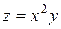 в точке М(1; 2) при
в точке М(1; 2) при  – приближенно.
– приближенно. – точно.
– точно.