 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Частные производные функций многих переменных. 12
Лекция 27. Основные понятия о функциях многих переменных. Частные производные, полный дифференциал функций нескольких переменных. Приложения полного дифференциала функций нескольких переменных. Частные производные и дифференциалы высших порядков функций нескольких переменных. Основные понятия. До сих пор, встречаясь с функциями, мы имели дело с функциями вида y = f(x), то есть с функциями одного аргумента (одной переменной) х. Однако многие теоретические и прикладные задачи требуют для своего решения использования функций нескольких переменных. А именно, функций вида z = f(x; y) – функций двух переменных; функций вида u = f(x; y; z) – функций трех переменных, и т.д. Причем в реальных теоретических и прикладных задачах функции многих переменных встречаются даже чаще, чем функции одной переменной. Действительно, в реальных условиях каждая исследуемая величина у зависит, вообще говоря, от многих величин (х1; х2; …; xn), то есть представляет собой функцию y = f(х1; х2; …; xn) многих переменных. И только если влияние на величину у какой-то одной из этих переменных (например, х1) существенно больше, чем влияние остальных, то пренебрегая этими остальными переменными, получим функцию y = f(х1) одной переменной. Это простейший и наиболее легко анализируемый случай, который мы и изучали до сих пор. Например, путь s, проходимый свободно падающим телом, объективно зависит от многих величин: от времени падения t, плотности воздуха r, массы т и объема V тела, и т.д. То есть s = f(t; r; m; V; …) – функция многих переменных. И только пренебрегая влиянием на путь s сопротивления воздуха, а значит, исключая влияние на s величин r, т, V и т.д., получим известную еще из школьной физики зависимость Впрочем, исследуемая величина может и существенно зависеть от нескольких других величин, так что влиянием ни одной из них на исследуемую величину пренебречь нельзя. Например, ток I, проходящий через некоторое сопротивление R, существенно зависит от величины этого сопротивления и напряжения U на концах этого сопротивления: Такие примеры указывают на то, что в математике должен быть разработан аппарат исследования функций многих переменных. Такой аппарат давно разработан. Во многом он использует те же понятия и идеи, что и аппарат исследования функций одной переменной. Однако есть и существенные различия. В чем они состоят – об этом ниже. Основные понятия, связанные с функциями одной переменной.
Пусть y = f(x) – произвольная функция одной переменной: х – независимая переменная (аргумент), у – функция. Как всем известно, суть этой функции такова: х ® у (по х находится у). Множество D всех тех значений независимой переменной х, для которых можно найти у, называется областью определения функции y = f(x). Если функцию y можно найти для любого х (-¥ < x < +¥), то есть для любой точки х числовой оси ох, то область D определения этой функции занимает всю ось ох. Если же это возможно не для любого х, то область определения D функции y = f(x) представляет собой некоторую часть оси ох – например, отрезок [a; b] (рис. 1).
Характер изменения функции у при изменении ее аргумента х очень наглядно демонстрируем график функции, который в принципе представляет собой некоторую линию L на плоскости хоу (рис. 2). График функции y = f(x) (линия L) состоит из точек плоскости, координаты (x; y) которых удовлетворяют уравнению y = f(x). Точки (M1; M2; M3) – вершины и впадины графика функции, а их проекции на ось ох (на область определения D этой функции) называются, как мы знаем, точками экстремума функции (точками ее максимума и минимума). Известна и схема нахождения этих важнейших для функции y = f(x) точек через ее производную y´ = f´(x) ( см. лекция 26 ).
Основные понятия, связанные с функциями двух переменных
Пусть z = f(x; y) – произвольная функция двух переменных: х и у – независимые переменные, z – функция от этих переменных. Суть такой функции аналогична сути функции одной переменной: (х; у) ® z (по х и у находится z). Множество D всех тех пар значений независимых переменных (x; y), для которых можно найти зависимую переменную (функцию) z, называется областью определения функции z = f(x; y). Так как каждая пара чисел (x; y) представляет собой некоторую точку плоскости хоу, то область определения D функции z = f(x; y) состоит из точек этой плоскости. Если функция z = f(x; y) определена для любых (x; y), то область D будет занимать всю плоскость хоу. А если не для любых - то какую-либо ее часть. И для каждой точки M(x; y) области D можно Для наглядности рисунку 3 можно придать и какой-нибудь реальный наглядный смысл. Например, можем считать, что D – неравномерно нагретая пластинка, а z = f(x; y) – температура в точках M(x; y) этой пластинки. Или на пластинку D что-то давит, а z = f(x; y) – давление на точки M(x; y) этой пластинки. Или даже D – поле, чем-нибудь засеянное, а z = f(x; y) – урожайность посеянной культуры в точках этого поля. И так далее.
То есть графиком произвольной функции z = f(x; y) (геометрической иллюстрацией)в принципе является некоторая поверхность S в пространстве. Итак, графиком функции z=f(x, y) в пространстве XYZ является поверхность, представляющая собой геометрическое место точек (х, у, f(х, у)), когда точка (х, у) пробегает область определения функции. Эта поверхность может иметь вершины и впадины (N1; N2; N3; …). Их проекции (M1; M2; M3; …) на плоскость хоу (на область определения D) называются точками экстремума функции (точками ее максимума и минимума). Сравнивая рис.2 и 4, легко видеть и то общее, что имеется между точками экстремума функций одной и двух переменных, и в чем разница между ними. Есть и математическая схема нахождения точек экстремума функции z = f(x; y). Но об этом – позже. Пример 1. Если х и у могут принимать любые числовые значения, то переменные z=x2+y2, z=ln(1+x4+y5) и т. д. представляют собой аналитически заданные функции от х и у. Область определения каждой из них – множество всевозможных пар чисел (х, у). Пример 2. Объем конуса V есть функция его высоты H и радиуса основания R. Ее аналитическое выражение: Естественной областью определения аналитически заданной функции z=f(x, y)называется совокупность всех пар чисел (х, у), которым соответствуют действительные значения функции. Так, например, для функции z=ln(x2+y2-1) естественная область определения состоит из всех пар чисел (х, у), для которых х2+у
У функции ласть определения изображается множест- Рис.5 Рис.6. вом точек прямоугольника со сторонами х=±1, у=±2, поэтому мы будем говорить: функция
.  Рис.8. Рис.9
Пример 3, Для функции z=x2+y2 область определения – вся плоскость, а изображающая ее поверхность – параболоид вращения (рис. 7). Пример 4. функция Познакомимся еще с одним способом геометрической иллюстрации функций двух переменных. Будем называть линией уровня функции z=f(x,y) геометрическое место точек (х, у) плоскости, в которых функция принимает одно и то же значение С. Линию уровня можно построить, спроектировав на плоскость XOY множество точек пространства XYZ, лежащих в пересечении поверхности изображающей функцию z=f(x, y), и плоскости z=C (рис. 9). Уравнение линии уровня имеет вид: f(x, y)=C. Изменяя С, мы будем получать различные линии уровня для данной функции. Если положить С=С1, С2,…,Сп,…, выбрав эти числа в арифметической прогрессии с разностью h, то мы получим ряд линий уровня, по взаимному расположению которых можно судить о характере изменения функции (рис. 7). В частности, там, где линии гуще, функция изменяется быстрее (поверхность, изображающая функцию, идет круче), а там, где линии уровня располагаются реже, функция изменяется медленнее (соответствующая поверхность будет более пологой). Кроме того, отметки на линиях уровня дают непосредственно значения функции в точках этих линий. Выбирая h достаточно малым, можно таким образом получить довольно точное представление о поведении функции.
Рис. 10. Пример 5. Функция z=x2+y2 имеет линиями окружности х2+у2=С, 0≤С<+∞. Полагая, например, С=0, 1, 2, 3,…, получаем соответствующие линии уровня, сгущающиеся с ростом С. при С=0 окружность вырождается в точку (0, 0) (рис. 11). Пример 6. Для функции z=x+y линиями уровня будут прямые х+у=С, -∞<С<+∞. Полагая С=0, ±1, ±2, …, получаем ряд линий уровня (рис. 12). Линии уровня часто используются при составлении географических карт (линии уровня – линии, в которых высота точек земной поверхности над уровнем моря одинакова), при составлении метеорологических карт (линии уровня – линии одинаковых температур (изотермы), линии равного давления (изобары)) и т. д.
Рис.11. Рис.12.
В заключение остановимся на понятиях предела функции двух переменных и её непрерывности. Они практически аналогичны тем же самым понятиям для функции одной переменной. Окрестностью радиуса r точки Число А называется пределом функции z=f(x,y) при Пусть точка
3. Основные понятия, связанные с функциями трех переменных
Для наглядности величину u можно представлять себе, например, как температуру в точках M(x; y; z) теперь уже пространственной области D. А можно, разумеется, эту величину u = f(x; y; z) трактовать и совершенно иначе. Например, считать, что u – прибыль предприятия, если продано x единиц продукции этого предприятия при цене у за единицу продукции и при затратах z на произведенную продукцию. И так далее. Отметим, что графически представить себе ход изменения функции трех переменных u = f(x; y; z) невозможно, ибо такие функции графика не имеют. Действительно, график функции u = f(x; y; z) должен состоять из точек N(x; y; z; u) с четырьмя координатами, где u = f(x; y; z). То есть из точек четырехмерного пространства, которое физически непредставимо (его используют в математике лишь как математическую абстракцию). 4.Основные понятии, связанные с функциями четырех И более переменных.
Пусть, например, функция u = f(x; y; z; t) – произвольная функция четырех переменных (x; y; z; t). Ее область определения D состоит из точек D(x; y; z; t) четырехмерного пространства, то есть наглядно не представима. Графика у этой функции, естественно, тоже нет. Но этой функции, как и функциям большего числа переменных, всегда можно придать самый разнообразный наглядный прикладной смысл. Например, функцию u = f(x; y; z; t) можно считать температурой в пространственной точке M(x; y; z) в момент времени t, когда эта температура меняется со временем (нестационарная температура). Или прибылью от продажи товара при количестве проданного товара х, цене единицы товара у, налоге с продаж z и налоге на прибыль t. Или еще как-нибудь. Естественно, чем от большего числа переменных зависит функция, тем сложнее изучать эту функцию. Наиболее простой случай функции многих переменных – это когда функция зависит лишь от двух переменных. Рассмотрением этого случая мы в основном в дальнейшем и ограничимся. Упражнения 1. Найти и изобразить на плоскости хоу области определения следующих функций:
Ответ:
2. Дана функция u = x + y + z. а) Найти область определения функции u. б) Определить те точки M(x; y; z) области определения функции, для которых u =1. Ответ: а) область определения функции u – все пространство xоyz; б) точки плоскости x + y + z = 1, которая пересекает оси ох, оу и оz соответственно в точках M1(1; 0; 0), M2(0; 1; 0), M3(0; 0; 1).
Частные производные функций многих переменных.
Пусть
называется частной производной функции z по переменной х. Аналогично определяется, при фиксированном х и переменном у, частная производная функции z = f(x; y) по переменной y:
Пример 7. Пусть
Пользуясь определением производной функции одной переменной, можем записать и математические определения частных производных функции z = f(x;y):
Если
Пример 8. Если
Совершенно аналогично определяются частные производные функций любого числа переменных. Все это – так называемые частные производные первого порядка. А если от них снова вычислить (взять) частные производные, то получим уже частные производные второго, третьего и т.д. порядков. Например, если
– частная производная второго порядка от z по х;
– частная производная второго порядка от z по y;
– смешанные частные производные второго порядка от z по х и у. Кстати, доказано, что если
То есть результат вычисления смешанных производных не зависит от порядка дифференцирования (если это дифференцирование возможно и в том, и в другом порядка). Пример 9. Пусть
Примечание. В обозначениях (1) – (7) для частных производных значок 12 |



 , представляющую собой функцию одной переменной t.
, представляющую собой функцию одной переменной t. (закон Ома). Еще пример: прибыль предприятия R существенно зависит от цены р единицы продукции этого предприятия, от количества q единиц проданной продукции, от денежных затрат z на производство и реализацию проданной продукции: R = pq – z. То есть величина R является функцией по меньшей мере трех переменных (p; q; z), каждая из которых существенна.
(закон Ома). Еще пример: прибыль предприятия R существенно зависит от цены р единицы продукции этого предприятия, от количества q единиц проданной продукции, от денежных затрат z на производство и реализацию проданной продукции: R = pq – z. То есть величина R является функцией по меньшей мере трех переменных (p; q; z), каждая из которых существенна. Иллюстрации, изображенной на рис. 1, можно для наглядности придать и какой-то реально осязаемый смысл. Например, можно себе представить, что отрезок [a; b] оси ох – это тонкий материальный стержень, неравномерно нагретый вдоль своей оси, а y = f(x) – температура в точке х этого отрезка. Впрочем, функции y =f(x) можно придать совершенно другой смысл. Например, можно считать, что y – объем произведенной продукции при затратах х на ее производство.
Иллюстрации, изображенной на рис. 1, можно для наглядности придать и какой-то реально осязаемый смысл. Например, можно себе представить, что отрезок [a; b] оси ох – это тонкий материальный стержень, неравномерно нагретый вдоль своей оси, а y = f(x) – температура в точке х этого отрезка. Впрочем, функции y =f(x) можно придать совершенно другой смысл. Например, можно считать, что y – объем произведенной продукции при затратах х на ее производство.
 найти значение величины z = f(x; y) ( одно или несколько ) (рис. 3). При этом переменные х и у называются независимыми переменными, или аргументами, а переменная z – зависимой переменной, или функцией. Множество значений функции z называется областью изменения этой функции. Если каждой паре чисел (х, у) из области определения функции соответствует одно значение – однозначной, в противном случае - многозначной. Так же как и для функций одной переменной, если не оговорено противное, мы будем предполагать, что рассматриваемые функции двух переменных однозначны. Сам закон соответствия может быть задан произвольным образом (аналитически, т. е. с помощью формул, выражающих z через х и у, таблично, графически, словесным образом и пр.). Математический анализ изучает преимущественно аналитически заданные функции.
найти значение величины z = f(x; y) ( одно или несколько ) (рис. 3). При этом переменные х и у называются независимыми переменными, или аргументами, а переменная z – зависимой переменной, или функцией. Множество значений функции z называется областью изменения этой функции. Если каждой паре чисел (х, у) из области определения функции соответствует одно значение – однозначной, в противном случае - многозначной. Так же как и для функций одной переменной, если не оговорено противное, мы будем предполагать, что рассматриваемые функции двух переменных однозначны. Сам закон соответствия может быть задан произвольным образом (аналитически, т. е. с помощью формул, выражающих z через х и у, таблично, графически, словесным образом и пр.). Математический анализ изучает преимущественно аналитически заданные функции. Характер изменения функции z = f(x; y) при изменении ее аргументов х и у (то есть при изменении точки M(х; y)) можно наглядно изобразить на графике функции. График функции z = f(x; y) состоит из точек N(x; y; z) пространства, для которых абсцисса х и ордината у – это координаты точек M(x;y) её области определения D, а аппликата находится по формуле z = f(x; y) (рис.4).
Характер изменения функции z = f(x; y) при изменении ее аргументов х и у (то есть при изменении точки M(х; y)) можно наглядно изобразить на графике функции. График функции z = f(x; y) состоит из точек N(x; y; z) пространства, для которых абсцисса х и ордината у – это координаты точек M(x;y) её области определения D, а аппликата находится по формуле z = f(x; y) (рис.4). . Область определения – всевозможные пары чисел (R, H), где R>0, H>0.
. Область определения – всевозможные пары чисел (R, H), где R>0, H>0. естественная область определения состоит из всех пар чисел, для которых
естественная область определения состоит из всех пар чисел, для которых 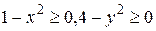 , т.е.
, т.е.  .
.
 В дальнейшем, если дополнительные ограничения на изменение независимых переменных постановкой задачи (как это было в примере 2) не накладываются, под областью определения аналитически заданной функции будем подразумевать ее естественную область определения. Выберем на плоскости прямоугольную систему координат ХОY и будем изображать пары чисел (х, у) точками плоскости с координатами х, у. Тогда область определения функции f(x, y) будет изображаться некоторым множеством точек М плоскости, в связи с чем функцию двух переменных часто называют функцией точки М плоскости и обозначают z=f(M), а ее область определения отождествляют с множеством изображающих ее точек. Так, для функции z=ln(x2+y2-1) область определения изображается множеством точек плоскости XOY, лежащих вне круга К с центром (0, 0) радиуса 1, поэтому мы будем говорить: функция z=ln(x2+y2-1) определена вне круга К (см. рис. 5).
В дальнейшем, если дополнительные ограничения на изменение независимых переменных постановкой задачи (как это было в примере 2) не накладываются, под областью определения аналитически заданной функции будем подразумевать ее естественную область определения. Выберем на плоскости прямоугольную систему координат ХОY и будем изображать пары чисел (х, у) точками плоскости с координатами х, у. Тогда область определения функции f(x, y) будет изображаться некоторым множеством точек М плоскости, в связи с чем функцию двух переменных часто называют функцией точки М плоскости и обозначают z=f(M), а ее область определения отождествляют с множеством изображающих ее точек. Так, для функции z=ln(x2+y2-1) область определения изображается множеством точек плоскости XOY, лежащих вне круга К с центром (0, 0) радиуса 1, поэтому мы будем говорить: функция z=ln(x2+y2-1) определена вне круга К (см. рис. 5).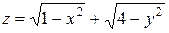 об-
об-
 имеет областью определения круг
имеет областью определения круг  и изображается нижней полусферой с центром О (0, 0, 0) радиуса R=1 (рис. 8).
и изображается нижней полусферой с центром О (0, 0, 0) радиуса R=1 (рис. 8).

 называется совокупность точек (x,y) удовлетворяющих неравенству
называется совокупность точек (x,y) удовлетворяющих неравенству  , т.е. совокупность всех точек, лежащих внутри круга радиуса r с центром в точке
, т.е. совокупность всех точек, лежащих внутри круга радиуса r с центром в точке  , если для любого числа
, если для любого числа 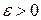 найдется число
найдется число  , зависящее от
, зависящее от  , такое, что для всех точек (x,y), отстоящее от точки
, такое, что для всех точек (x,y), отстоящее от точки  не более, чем на
не более, чем на  , выполняется неравенство
, выполняется неравенство  . Обозначается
. Обозначается  .
. .
. Пусть u = f(x; y; z) – произвольная функция трех переменных: x, y, z – независимые переменные, u – функция от этих переменных (зависимая переменная). Суть такой функции: (x; y; z)® u (по x, y, z находится u). Множество D всех тех троек значений независимых переменных (x, y, z), для которых можно найти зависимую переменную (функцию) u, называется областью определения функции u = f(x; y; z). Так как каждая тройка чисел (x, y, z) представляет собой некоторую точку пространства, то область D определения функции u = f(x; y; z) состоит из точек пространства. Эта область может занимать все пространство или какую-либо его часть. И для каждой точки M(x, y, z) области D можно найти значение величины u = f(x; y; z) (рис.13).
Пусть u = f(x; y; z) – произвольная функция трех переменных: x, y, z – независимые переменные, u – функция от этих переменных (зависимая переменная). Суть такой функции: (x; y; z)® u (по x, y, z находится u). Множество D всех тех троек значений независимых переменных (x, y, z), для которых можно найти зависимую переменную (функцию) u, называется областью определения функции u = f(x; y; z). Так как каждая тройка чисел (x, y, z) представляет собой некоторую точку пространства, то область D определения функции u = f(x; y; z) состоит из точек пространства. Эта область может занимать все пространство или какую-либо его часть. И для каждой точки M(x, y, z) области D можно найти значение величины u = f(x; y; z) (рис.13).
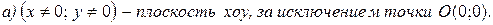


 – некоторая функция двух переменных. Если зафиксировать одну из переменных (например, у), то функция
– некоторая функция двух переменных. Если зафиксировать одну из переменных (например, у), то функция  ,
,
 . Тогда
. Тогда



 то
то
 – функция двух переменных, то
– функция двух переменных, то

 и
и 
 обе существуют, то они и равны:
обе существуют, то они и равны:
 . Тогда
. Тогда
 – с кривым хвостом! В этом его отличие от прямого значка d, применяемого в обозначения для обычных производных функций одной переменной.
– с кривым хвостом! В этом его отличие от прямого значка d, применяемого в обозначения для обычных производных функций одной переменной.