Структура общего решения линейного однородного уравнения
Определение 5. Фундаментальной системой решений линейного однородного дифференциального уравнения  -го порядка -го порядка  называется любая система называется любая система  линейно независимых решений этого уравнения. линейно независимых решений этого уравнения. Теорема 3 (структура общего решения линейного однородного уравнения). Пусть функции  образуют фундаментальную систему решений линейного однородного дифференциального уравнения образуют фундаментальную систему решений линейного однородного дифференциального уравнения  -го порядка -го порядка  . Тогда функция . Тогда функция  , (8) , (8)
где  произвольные постоянные, является общим решением этого уравнения. произвольные постоянные, является общим решением этого уравнения. ▲ Нужно проверить, что (8) удовлетворяет определению общего решения 7. При любых значениях постоянных  , ,  эта функция, согласно свойству 3. решений линейного однородного дифференциального уравнения, является решением уравнения эта функция, согласно свойству 3. решений линейного однородного дифференциального уравнения, является решением уравнения  . . Теперь проверим второе условие определения 7: зададим в точке  произвольные начальные условия произвольные начальные условия  , ,  , …, , …,  и покажем, что постоянные и покажем, что постоянные  можно подобрать так, чтобы функция (8) удовлетворяла этим начальным условиям. Имеем: можно подобрать так, чтобы функция (8) удовлетворяла этим начальным условиям. Имеем:  . (9) . (9)
(9) является системой  линейных уравнений с линейных уравнений с  неизвестными неизвестными  . Определитель этой системы – это определитель, составленный из коэффициентов при неизвестных . Определитель этой системы – это определитель, составленный из коэффициентов при неизвестных  , т.е. определитель Вронского , т.е. определитель Вронского  , который отличен от 0 в силу линейной независимости функций , который отличен от 0 в силу линейной независимости функций  . Но тогда система (9), как система . Но тогда система (9), как система  линейных уравнений с n неизвестными и определителем, не равным 0, имеет единственное решение. ■ линейных уравнений с n неизвестными и определителем, не равным 0, имеет единственное решение. ■ Таким образом, для нахождения общего решения уравнения (1) нужно знать фундаментальную систему его решений. Однако в общем случае методов нахождения такой фундаментальной системы не существует. Ниже будет описан способ нахождения фундаментальной системы решений для одного класса уравнений вида  . . Линейные однородные уравнения с постоянными коэффициентами В этом параграфе будет рассматриваться оператор вида  , (10) , (10)
где  , ,  постоянные действительные числа, и уравнение вида постоянные действительные числа, и уравнение вида  , , 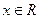 , или , или  . (11) . (11)
Уравнение (11) можно разделить на  , поэтому к нему применимы предыдущие рассуждения, и общее решение (11) ищется по формуле (8): , поэтому к нему применимы предыдущие рассуждения, и общее решение (11) ищется по формуле (8):  где где  произвольные постоянные, а произвольные постоянные, а  фундаментальная система решений. фундаментальная система решений. Для нахождения последней будем искать решения (11) в виде  , где , где  некоторое число. Подставляя некоторое число. Подставляя  в (11) и учитывая, что в (11) и учитывая, что  , имеем: , имеем: 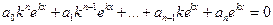 , или , или  . (12) . (12)
Т.е. функция  является решением уравнения (11) тогда и только тогда, когда число является решением уравнения (11) тогда и только тогда, когда число  является корнем уравнения (12). является корнем уравнения (12). Определение 6. Уравнение (12) называется характеристическим уравнением для дифференциального уравнения (11). Характеристическое уравнение (12) получается из дифференциального уравнения (11) заменой производной  на на  , ,  (под нулевой производной функции понимается сама эта функция). (под нулевой производной функции понимается сама эта функция). Определение 7. Левую часть характеристического уравнения (12) назовем характеристическим многочленом и обозначим  . . Уравнение (12), как и всякое алгебраическое уравнение степени  , имеет ровно , имеет ровно  корней с учетом их кратности. Рассмотрим следующие 4 случая: корней с учетом их кратности. Рассмотрим следующие 4 случая: 1. Все корни характеристического уравнения действительные и различные Пусть  эти корни. Этим корням соответствуют эти корни. Этим корням соответствуют  решений уравнения (11): решений уравнения (11):  , ,  , …, , …,  . Эти функции линейно независимы (см. пример выше), значит, они образуют фундаментальную систему решений уравнения (11), и общее решение этого уравнения задается формулой (8). . Эти функции линейно независимы (см. пример выше), значит, они образуют фундаментальную систему решений уравнения (11), и общее решение этого уравнения задается формулой (8). Пример. Решить дифференциальное уравнение  . .
Решение. Характеристическое уравнение имеет вид:  . Решаем это уравнение: . Решаем это уравнение:  Этим трем действительным различным корням соответствуют три решения из фундаментальной системы решений: Этим трем действительным различным корням соответствуют три решения из фундаментальной системы решений: 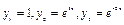 , и общее рашение исходного уравнения имеет вид: , и общее рашение исходного уравнения имеет вид:  . . 2. Корни характеристического уравнения разные, но среди них есть комплексные Так как в предыдущих рассуждениях нигде не использовалось, что корни характеристического уравнения и коэффициенты  в решениях вида в решениях вида  действительные числа, то все результаты пункта 1. справедливы и в случае таких комплексных чисел, однако в фундаментальной системе решений часть функций окажется тогда комплекснозначной. Чтобы от таких функций перейти к функциям с действительными значениями, поступим следующим образом. действительные числа, то все результаты пункта 1. справедливы и в случае таких комплексных чисел, однако в фундаментальной системе решений часть функций окажется тогда комплекснозначной. Чтобы от таких функций перейти к функциям с действительными значениями, поступим следующим образом. Пусть  корень характеристического уравнения (12) кратности 1. Так как это уравнение с действительными коэффициентами, то корень характеристического уравнения (12) кратности 1. Так как это уравнение с действительными коэффициентами, то  тоже корень уравнения (12) кратности 1. Этим корням соответствуют следующие решения уравнения (11): тоже корень уравнения (12) кратности 1. Этим корням соответствуют следующие решения уравнения (11): 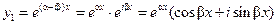 и и
 . .
Так как любая линейная комбинация (даже с комплексными коэффициентами) решений линейного однородного уравнения тоже является решением этого уравнения, то решениями (11) будут и функции  и и  . .
Покажем, что если в фундаментальной системе решений  заменить заменить 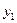 и и 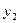 на такие их линейные комбинации, то система останется фундаментальной. Для этого, согласно определению фундаментальной системы решений 5, достаточно доказать, что функции новой системы будут линейно независимыми. Приравняем к 0 линейную комбинацию таких функций: на такие их линейные комбинации, то система останется фундаментальной. Для этого, согласно определению фундаментальной системы решений 5, достаточно доказать, что функции новой системы будут линейно независимыми. Приравняем к 0 линейную комбинацию таких функций:   . .
Тогда    . .
Так как  линейно независимы, то все коэффициенты их линейной комбинации, равной 0, будут равны 0, т.е. линейно независимы, то все коэффициенты их линейной комбинации, равной 0, будут равны 0, т.е. 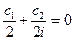 ; ;  ; ;  ;…; ;…;  . Складывая и вычитая два первых равенства, имеем . Складывая и вычитая два первых равенства, имеем  и и  , ,  , что и требовалось доказать. , что и требовалось доказать. Так же можно поступить с любой другой парой комплексно сопряженных корней кратности 1 уравнения (12). Пример. Решить дифференциальное уравнение  . . Решение. Запишем характеристическое уравнение:  . Комплексные корни этого уравнения . Комплексные корни этого уравнения  имеют кратность 1, и общее решение дифференциального уравнение пишется в виде имеют кратность 1, и общее решение дифференциального уравнение пишется в виде  . .
3. Среди корней характеристического уравнения есть действительные кратные Пусть 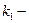 действительный корень характеристического уравнения (12) кратности действительный корень характеристического уравнения (12) кратности  . Согласно предыдущему, ему соответствует решение уравнения (11) . Согласно предыдущему, ему соответствует решение уравнения (11)  . Но чтобы сохранить количество решений . Но чтобы сохранить количество решений 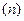 в фундаментальной системе, этому корню должно соответствовать в фундаментальной системе, этому корню должно соответствовать  решений. решений. Оказывается, что такими решениями будут функции  , ,  , ,  , …, , …, 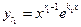 . .
1) Эти функции являются решениями уравнения (11). Проверим это в случае  , т.е. при , т.е. при  , ,  , ,  ,…, ,…,  . . В этом случае характеристическое уравнение (12) имеет вид  , где , где  , или , или
 , где , где  , ,
тогда соответствующее дифференциальное уравнение (11) имеет вид  , ,  , ,
и, очевидно, что все наши функции удовлетворяют этому уравнению, так как все встречающиеся в нем производные этих функций равны 0. Случай  сводится к случаю сводится к случаю  путем замены путем замены  , где , где  новая неизвестная функция. Рассмотрение такой замены, однако, требует достаточно громоздких выкладок, которые мы здесь приводить не будем. новая неизвестная функция. Рассмотрение такой замены, однако, требует достаточно громоздких выкладок, которые мы здесь приводить не будем. 2) Теперь проверим, что полученные решения линейно независимы. Приравняем к 0 (тождественно на любом конечном или бесконечном промежутке) произвольную линейную комбинацию этих решений и докажем, что все коэффициенты этой линейной комбинации обязательно равны 0. Имеем:  
(последний переход уже был разобран выше). Так же можно поступить с любым другим действительным кратным корнем характеристического уравнения. Можно проверить, что вся полученная таким образом система решений будет линейно независимой. Пример. Решитьдифференциальное уравнение  . . Решение. Характеристическое уравнение имеет вид:  . Решаем это уравнение: . Решаем это уравнение:  ; ;  ; ;  ; ;  , ,  . В соответствии с изложенным выше, общее решение дифференциального уравнения имеет вид . В соответствии с изложенным выше, общее решение дифференциального уравнения имеет вид  . . 4. Среди корней характеристического уравнения есть комплексные кратные Так как в рассуждениях пункта 3. не использовалась действительность корней характеристического уравнения и коэффициентов  в решениях вида в решениях вида  , то результаты 3. справедливы и в случае комплексных чисел, однако при этом часть функций в фундаментальной системе решений окажется комплекснозначными. Чтобы от них перейти к функциям с действительными значениями, поступим аналогично пункту 2. и получим новую фундаментальную систему решений: , то результаты 3. справедливы и в случае комплексных чисел, однако при этом часть функций в фундаментальной системе решений окажется комплекснозначными. Чтобы от них перейти к функциям с действительными значениями, поступим аналогично пункту 2. и получим новую фундаментальную систему решений:  и и  , ,  . .
Пример. Решить дифференциальное уравнение  . . Решение. Характеристическое уравнение имеет вид:  , или , или  . Корни этого уравнения: . Корни этого уравнения:  , ,  . В соответствии с результатами пункта 4, общим решением дифференциального уравнения будет функция . В соответствии с результатами пункта 4, общим решением дифференциального уравнения будет функция  . . Подведем итог: Общее решение уравнения 
имеет вид  , ,
где  произвольные постоянные, а произвольные постоянные, а  фундаментальная система решений уравнения, которая ищется следующим образом: фундаментальная система решений уравнения, которая ищется следующим образом: составляем характеристическое уравнение 
Это уравнение имеет ровно  корней (с учетом кратности). Этим корням соответствуют следующие корней (с учетом кратности). Этим корням соответствуют следующие  функций в фундаментальной системе решений: функций в фундаментальной системе решений: 1. Каждому действительному корню  кратности 1 соответствует решение кратности 1 соответствует решение  . . 2. Каждой паре комплексно сопряженных корней  и и  , кратности 1 каждый, соответствуют два решения , кратности 1 каждый, соответствуют два решения  и и  . . 3. Каждому действительному корню  кратности кратности  соответствуют соответствуют  решений решений  , ,  , ,  , …, , …,  . . 4. Каждой паре комплексно сопряженных корней  и и  кратности кратности  каждый, соответствует каждый, соответствует  решений решений  , ,  , ,  , ,  ,…, ,…,  , ,  . . Лекция 3 НЕОДНОРОДНЫЕ ЛИНЕЙНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ В этом параграфе, как и выше, под  понимается линейный дифференциальный оператор вида понимается линейный дифференциальный оператор вида  , (1) , (1)
где все коэффициенты  , ,  определены и непрерывны на некотором интервале определены и непрерывны на некотором интервале  , и рассматривается так называемое неоднородное уравнение , и рассматривается так называемое неоднородное уравнение  , где , где  также определена и непрерывна на также определена и непрерывна на  , или , или  . (2) . (2)
Уравнение вида  или или  (3) (3)
называется однородным линейным уравнением, соответствующим уравнению (2). Общее решение (2) находится в соответствии с теоремой 3 предыдущей лекции. Теорема 1 (структура общего решения линейного неоднородного уравнения).Пусть  общее решение однородного уравнения (3) (здесь общее решение однородного уравнения (3) (здесь  фундаментальная система решений этого уравнения, а фундаментальная система решений этого уравнения, а 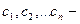 произвольные постоянные), а произвольные постоянные), а  частное решение неоднородного уравнения (2) (т.е. одно из решений этого уравнения). Тогда функция частное решение неоднородного уравнения (2) (т.е. одно из решений этого уравнения). Тогда функция  (4) (4)
является общим решением уравнения (2). Т.е. общее решение линейного неоднородного уравнения есть сумма общего решения соответствующего однородного уравнения и частного решения исходного неоднородного уравнения. ▲ Нужно проверить, что функция (4) удовлетворяет определению общего решения дифференциального уравнения. Как и  , эта функция зависит от , эта функция зависит от  и и  произвольных постоянных произвольных постоянных  . При любых значениях этих постоянных функция (4) является решением уравнения (2): . При любых значениях этих постоянных функция (4) является решением уравнения (2):   . . Теперь в точке  зададим произвольные начальные условия зададим произвольные начальные условия  , ,  , … , , … ,  и покажем, что постоянные и покажем, что постоянные  можно подобрать так, чтобы функция (4) удовлетворяла этим начальным условиям. Имеем: можно подобрать так, чтобы функция (4) удовлетворяла этим начальным условиям. Имеем:  . (5) . (5)
Система (5) является системой  линейных уравнений с линейных уравнений с  неизвестным неизвестным  и правыми частями и правыми частями  , ,  , … , , … ,  . Определитель этой системы – это определитель Вронского . Определитель этой системы – это определитель Вронского  , который отличен от 0 в силу линейной независимости функций , который отличен от 0 в силу линейной независимости функций  . Значит, система (5) имеет единственное решение. ■ . Значит, система (5) имеет единственное решение. ■ Приведем здесь еще одну теорему, которая в некоторых случаях облегчает нахождение частного решения неоднородного уравнения. Теорема 2. Пусть  частное решение уравнения частное решение уравнения  , а , а  частное решение уравнения частное решение уравнения  . Тогда . Тогда  частное решение уравнения частное решение уравнения  . . ▲  . ■ . ■ В соответствии с теоремой 1, для нахождения общего решения уравнения (2) нужно знать фундаментальную систему решений соответствующего однородного уравнения (3) (ее мы умеем находить для уравнений с постоянными коэффициентами) и частное решение данного неоднородного уравнения. Неоднородные линейные уравнения с постоянными коэффициентами и правой частью специального вида В этом параграфе коэффициенты линейного оператора  –постоянные действительные числа: –постоянные действительные числа:  , ,  . .
Тогда неоднородное  и соответствующее однородное и соответствующее однородное  уравнения из предыдущего параграфа будут иметь вид: уравнения из предыдущего параграфа будут иметь вид:  (6) (6)
и  , , 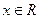 . (7) . (7)
Эти уравнения можно разделить на  , поэтому сюда применима теорема 1, и общее решение (6) будет иметь вид (4): , поэтому сюда применима теорема 1, и общее решение (6) будет иметь вид (4): 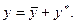 Частное решение неоднородного уравнения (6) будет искаться при следующих двух правых частях  (которые называются правыми частями специального вида): (которые называются правыми частями специального вида): 1.  , где , где  многочлен степени многочлен степени  . . Пусть число  является корнем характеристического уравнения для однородного уравнения (7) кратности является корнем характеристического уравнения для однородного уравнения (7) кратности  (если (если  не является корнем этого уравнения, то мы будем считать, что не является корнем этого уравнения, то мы будем считать, что  ). ). а) Сначала рассмотрим случай  , т.е. , т.е.  . . В этом случае естественно искать частное решение неоднородного уравнения (6)  в виде в виде  , где , где  многочлен некоторой степени многочлен некоторой степени  . Подставим такую функцию в уравнение (6), которое в данном случае (см. выше) имеет вид . Подставим такую функцию в уравнение (6), которое в данном случае (см. выше) имеет вид  , , 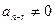 . . Имеем:  . (8) . (8)
В этой формуле 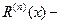 многочлен степени многочлен степени  , ,  многочлен степени многочлен степени  , … , , … ,  многочлен степени многочлен степени  . Тогда ( . Тогда ( 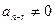 ) левая часть формулы (8) есть многочлен степени ) левая часть формулы (8) есть многочлен степени  . Но правая часть этой формулы есть многочлен степени . Но правая часть этой формулы есть многочлен степени  , значит, , значит, 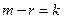 , ,  . . В левую часть формулы (8) не войдут коэффициенты многочлена  при при  (так как эти коэффициенты «пропадут» при нахождении производных (так как эти коэффициенты «пропадут» при нахождении производных  порядка порядка  и выше), значит, эти коэффициенты можно взять любыми. Взяв их равными 0, имеем: и выше), значит, эти коэффициенты можно взять любыми. Взяв их равными 0, имеем:   , ,
где  многочлен степени многочлен степени  с неопределенными коэффициентами (т.е. коэффициентами, которые нам еще надо найти). с неопределенными коэффициентами (т.е. коэффициентами, которые нам еще надо найти). б) Теперь рассмотрим случай произвольного  . . Такой случай сводится к случаю а) путем замены  , где, , где,  новая неизвестная функция. Опуская довольно громоздкие выкладки, получим частное решение уравнения для новая неизвестная функция. Опуская довольно громоздкие выкладки, получим частное решение уравнения для 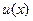  , где , где  – многочлен степени – многочлен степени  с неопределенными коэффициентами. Отсюда частное решение (6) можно искать в виде с неопределенными коэффициентами. Отсюда частное решение (6) можно искать в виде  . (9) . (9)
Подставляя функцию (9) в уравнение (6) и сокращая это уравнение на  , получим тождественное равенство (на , получим тождественное равенство (на  ) двух многочленов степени ) двух многочленов степени  . Необходимым и достаточным условием такого равенства является совпадение коэффициентов этих многочленов при одинаковых степенях . Необходимым и достаточным условием такого равенства является совпадение коэффициентов этих многочленов при одинаковых степенях  . Приравнивая эти коэффициенты, получим систему . Приравнивая эти коэффициенты, получим систему  уравнений с уравнений с  неизвестными, которая, как можно доказать, всегда имеет единственное решение. неизвестными, которая, как можно доказать, всегда имеет единственное решение. Таким образом, если  , то частное решение неоднородного уравнения (6) ищется по формуле (9), в которой , то частное решение неоднородного уравнения (6) ищется по формуле (9), в которой  многочлен степени многочлен степени  с неопределенными коэффициентами, а с неопределенными коэффициентами, а  кратность кратность  как корня характеристического уравнения для соответствующего однородного уравнения (7), или сколько раз как корня характеристического уравнения для соответствующего однородного уравнения (7), или сколько раз  , взятое из правой части уравнения (6), встречается среди корней характеристического уравнения. , взятое из правой части уравнения (6), встречается среди корней характеристического уравнения. Пример. Решить дифференциальное уравнение  . . Решение. Характеристическое уравнение для соответствующего однородного уравнения имеет вид  . Корни этого уравнения . Корни этого уравнения  , , 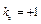 , и общее решение однородного уравнения , и общее решение однородного уравнения  . Теперь ищем частное решение исходного уравнения: . Теперь ищем частное решение исходного уравнения:  , ,  , ,  , и , и  . Находим производные этой функции и подставляем в исходное уравнение (для удобства записи опуская символ *): . Находим производные этой функции и подставляем в исходное уравнение (для удобства записи опуская символ *): 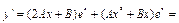 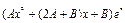 ; ;  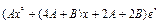 ; теперь ; теперь
  ; ;
 ; ;  . .
Приравниваем коэффициенты при одинаковых степенях х в левой и правой частях этого равенства:   . Из этой системы . Из этой системы  ; ;  ; ;  . В итоге, . В итоге,   . .
2.  , где , где  и и  многочлены степени многочлены степени  и и  соответственно с действительными коэффициентами (это обобщение случая 1, который получается отсюда при соответственно с действительными коэффициентами (это обобщение случая 1, который получается отсюда при  ). ). Можно показать, что вэтом случае частное решение неоднородного уравнения (6) следует искать по формуле  , (10) , (10)
где  и и  многочлены степени многочлены степени  с неопределенными (действительными) коэффициентами с неопределенными (действительными) коэффициентами  , а , а  – кратность – кратность 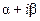 как корня характеристического уравнения для соответствующего однородного уравнения (7), или сколько раз как корня характеристического уравнения для соответствующего однородного уравнения (7), или сколько раз 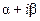 , взятое из правой части уравнения (6), встречается среди корней характеристического уравнения. , взятое из правой части уравнения (6), встречается среди корней характеристического уравнения. Подставляя решение вида (10) в уравнение (6), после сокращения на  получаем тождественное равенство (на получаем тождественное равенство (на  ) двух функций. Приравнивая коэффициенты при ) двух функций. Приравнивая коэффициенты при  и и  в обеих частях этого равенства (такие функции линейно независимы), получаем систему уравнений, из которой единственным образом находим коэффициенты многочленов в обеих частях этого равенства (такие функции линейно независимы), получаем систему уравнений, из которой единственным образом находим коэффициенты многочленов  и и 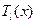 . . Пример. Решить диффененциальное уравнение  . . Решение. Соответствующее однородное уравнение  . Его характеристическое уравнение имеет вид . Его характеристическое уравнение имеет вид  , или , или  . Отсюда . Отсюда  и и  . Общее решение исходного уравнения: . Общее решение исходного уравнения:  . Находим частное решение исходного уравнения: . Находим частное решение исходного уравнения: 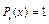 , , 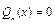 , ,  ; ;  , ,  , ,  ; это число не является корнем характеристического уравнения, поэтому ; это число не является корнем характеристического уравнения, поэтому  и и  . Отсюда (символ * для удобства записи опускаем) . Отсюда (символ * для удобства записи опускаем)  , ,  , ,  . Подставляем в исходное уравнение: . Подставляем в исходное уравнение:  ; ;  . Приравниваем коэффициенты при . Приравниваем коэффициенты при  и и  в левой и правой частях: в левой и правой частях:  Отсюда Отсюда  , ,  и и  . . Этот пример показывает, что независимо от наличия в правой части линейного дифференциального уравнения обеих функций  и и  или только одной из них, в решении вида (10) должны быть обе эти функции. или только одной из них, в решении вида (10) должны быть обе эти функции. Замечание. Если правая часть уравнения (6) является суммой двух или большего числа функций специального вида, то для нахождения частного решения этого уравнения удобно использовать упомянутую выше теорему 2. Метод вариации произвольных постоянных Теперь вернемся к общему виду линейного неоднородного дифференциального уравнения. Пусть  (1) (1)
и неоднородное и соответствующее однородное уравнения имеют вид  , ,  (2) (2)
 , ,  . (3) . (3)
Общее решение уравнения (2) имеет вид  (4) (4)
где  (11) (11)
– общее решение уравнения (3) (  фундаментальная система решений этого уравнения), а фундаментальная система решений этого уравнения), а  частное решение уравнения (2). частное решение уравнения (2). Метод вариации произвольных постоянных заключается в нахождении  по той же формуле (11), считая, что в ней коэффициенты по той же формуле (11), считая, что в ней коэффициенты  являются функциями являются функциями  : : 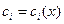 , ,  . . При подстановке такой функции в уравнение (2) получим одно уравнение с  неизвестными: неизвестными:  . Остальные . Остальные  уравнения мы допишем наиболее удобным для нас способом. Имеем: уравнения мы допишем наиболее удобным для нас способом. Имеем: 

Потребуем, чтобы  (это 1-е уравнение) (это 1-е уравнение) 
Потребуем, чтобы 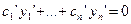 (это 2-е уравнение) (это 2-е уравнение) ………………………………………………………………………………….. (12) 
Потребуем, чтобы  (это (это  -ое уравнение) -ое уравнение) 
Последнее  -ое уравнение получается после подстановки всех этих функций в формулу (2). Для этого надо умножить последнее из равенств (12) на 1, предпоследнее – на -ое уравнение получается после подстановки всех этих функций в формулу (2). Для этого надо умножить последнее из равенств (12) на 1, предпоследнее – на  , …, второе – на , …, второе – на 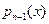 , первое – на , первое – на  (все эти множители приведены в столбце слева), и все полученные новые равенства сложить. Собирая вместе члены с (все эти множители приведены в столбце слева), и все полученные новые равенства сложить. Собирая вместе члены с  , получим: , получим:  . (13) . (13)
Так как  решения (3), то решения (3), то  , ,  , …, , …,  , и уравнение (13) приобретает вид , и уравнение (13) приобретает вид  . (14) . (14)
Теперь выпишем систему уравнений для  : :  . (15) . (15)
(15) – это система  линейных уравнений с линейных уравнений с  неизвестными неизвестными  . Ее легко запомнить: коэффициентами являются – в 1-м уравнении . Ее легко запомнить: коэффициентами являются – в 1-м уравнении  , во 2-м , во 2-м  , в 3-м , в 3-м  и т. д.; правые части, кроме последней ( и т. д.; правые части, кроме последней (  ой), равны 0, а последняя правая часть равна ой), равны 0, а последняя правая часть равна  . . Определитель системы (15) есть определитель Вронского функций   , который отличен от 0 во всех точках интервала , который отличен от 0 во всех точках интервала  , так как функции , так как функции  линейно независимы на этом интервале. Значит, система (15) имеет единственное решение линейно независимы на этом интервале. Значит, система (15) имеет единственное решение  , ,  , …, , …,  . . Первообразные для этих функций и являются нужными нам коэффициентами в формуле (11). Пример. Решить дифференциальное уравнение  . . Решение. Соответствующее однородное уравнение имеет вид  . Характеристическое уравнение . Характеристическое уравнение  имеет корни имеет корни  , ,  , ,  , и общее решение имеет вид , и общее решение имеет вид  . Теперь ищем частное решение . Теперь ищем частное решение  исходного уравнения по той же формуле, считая, что в ней исходного уравнения по той же формуле, считая, что в ней  , , 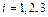 . Система (15) выглядит так: . Система (15) выглядит так:  . Складывая 2-е и 3-е уравнения, имеем: . Складывая 2-е и 3-е уравнения, имеем:  ; ;  . .
Подставим 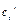 во 2-е уравнение: во 2-е уравнение: 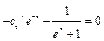 ; ;  . Подставим . Подставим  и и 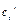 в 1-е уравнение: в 1-е уравнение:  . Теперь находим сами коэффициенты . Теперь находим сами коэффициенты 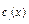 (произвольные постоянные не пишем, так как находим лишь одно частное решение неоднородного уравнения): (произвольные постоянные не пишем, так как находим лишь одно частное решение неоднородного уравнения):   ; ;
 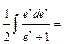   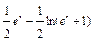 ; ;
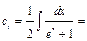    . .
Значит,  и и  . .
Метод вариации произвольных постоянных в принципе применим для любых линейных неоднородных уравнений (даже с коэффициентами, зависящими от  ). Однако для произвольных таких уравнений нет общего метода решения соответствующих однородных уравнений, поэтому этот метод применяется для решения уравнений с постоянными коэффициентами и правой частью, не являющейся функцией специального вида. При правых же частях специального вида применяется более простой (в частности, не содержащий операции интегрирования) метод, изложенный выше. ). Однако для произвольных таких уравнений нет общего метода решения соответствующих однородных уравнений, поэтому этот метод применяется для решения уравнений с постоянными коэффициентами и правой частью, не являющейся функцией специального вида. При правых же частях специального вида применяется более простой (в частности, не содержащий операции интегрирования) метод, изложенный выше.
| 
 -го порядка
-го порядка  называется любая система
называется любая система  образуют фундаментальную систему решений линейного однородного дифференциального уравнения
образуют фундаментальную систему решений линейного однородного дифференциального уравнения  , (8)
, (8) произвольные постоянные, является общим решением этого уравнения.
произвольные постоянные, является общим решением этого уравнения. ,
,  эта функция, согласно свойству 3. решений линейного однородного дифференциального уравнения, является решением уравнения
эта функция, согласно свойству 3. решений линейного однородного дифференциального уравнения, является решением уравнения  произвольные начальные условия
произвольные начальные условия  ,
,  , …,
, …,  и покажем, что постоянные
и покажем, что постоянные  . (9)
. (9) . Определитель этой системы – это определитель, составленный из коэффициентов при неизвестных
. Определитель этой системы – это определитель, составленный из коэффициентов при неизвестных  , т.е. определитель Вронского
, т.е. определитель Вронского  , который отличен от 0 в силу линейной независимости функций
, который отличен от 0 в силу линейной независимости функций  , (10)
, (10) ,
,  постоянные действительные числа, и уравнение вида
постоянные действительные числа, и уравнение вида  ,
, 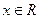 , или
, или . (11)
. (11) , поэтому к нему применимы предыдущие рассуждения, и общее решение (11) ищется по формуле (8):
, поэтому к нему применимы предыдущие рассуждения, и общее решение (11) ищется по формуле (8):  где
где  произвольные постоянные, а
произвольные постоянные, а  фундаментальная система решений.
фундаментальная система решений. , где
, где  некоторое число. Подставляя
некоторое число. Подставляя  , имеем:
, имеем: 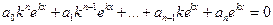 , или
, или . (12)
. (12) является корнем уравнения (12).
является корнем уравнения (12). на
на  ,
,  .
. эти корни. Этим корням соответствуют
эти корни. Этим корням соответствуют  ,
,  , …,
, …,  . Эти функции линейно независимы (см. пример выше), значит, они образуют фундаментальную систему решений уравнения (11), и общее решение этого уравнения задается формулой (8).
. Эти функции линейно независимы (см. пример выше), значит, они образуют фундаментальную систему решений уравнения (11), и общее решение этого уравнения задается формулой (8). .
. . Решаем это уравнение:
. Решаем это уравнение:  Этим трем действительным различным корням соответствуют три решения из фундаментальной системы решений:
Этим трем действительным различным корням соответствуют три решения из фундаментальной системы решений: 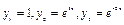 , и общее рашение исходного уравнения имеет вид:
, и общее рашение исходного уравнения имеет вид:  .
. корень характеристического уравнения (12) кратности 1. Так как это уравнение с действительными коэффициентами, то
корень характеристического уравнения (12) кратности 1. Так как это уравнение с действительными коэффициентами, то  тоже корень уравнения (12) кратности 1. Этим корням соответствуют следующие решения уравнения (11):
тоже корень уравнения (12) кратности 1. Этим корням соответствуют следующие решения уравнения (11):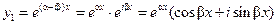 и
и .
. и
и  .
.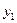 и
и 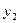 на такие их линейные комбинации, то система останется фундаментальной. Для этого, согласно определению фундаментальной системы решений 5, достаточно доказать, что функции новой системы будут линейно независимыми. Приравняем к 0 линейную комбинацию таких функций:
на такие их линейные комбинации, то система останется фундаментальной. Для этого, согласно определению фундаментальной системы решений 5, достаточно доказать, что функции новой системы будут линейно независимыми. Приравняем к 0 линейную комбинацию таких функций:
 .
.

 .
.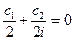 ;
;  ;
;  ;…;
;…;  . Складывая и вычитая два первых равенства, имеем
. Складывая и вычитая два первых равенства, имеем  и
и  ,
,  , что и требовалось доказать.
, что и требовалось доказать. .
. . Комплексные корни этого уравнения
. Комплексные корни этого уравнения  имеют кратность 1, и общее решение дифференциального уравнение пишется в виде
имеют кратность 1, и общее решение дифференциального уравнение пишется в виде .
.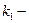 действительный корень характеристического уравнения (12) кратности
действительный корень характеристического уравнения (12) кратности  . Согласно предыдущему, ему соответствует решение уравнения (11)
. Согласно предыдущему, ему соответствует решение уравнения (11) 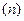 в фундаментальной системе, этому корню должно соответствовать
в фундаментальной системе, этому корню должно соответствовать  ,
,  , …,
, …, 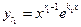 .
. , т.е. при
, т.е. при  ,
,  ,
,  ,…,
,…,  .
. , где
, где  , или
, или , где
, где  ,
, ,
,  сводится к случаю
сводится к случаю  путем замены
путем замены  , где
, где  новая неизвестная функция. Рассмотрение такой замены, однако, требует достаточно громоздких выкладок, которые мы здесь приводить не будем.
новая неизвестная функция. Рассмотрение такой замены, однако, требует достаточно громоздких выкладок, которые мы здесь приводить не будем.

 .
. . Решаем это уравнение:
. Решаем это уравнение:  ;
;  ;
;  ;
;  ,
,  . В соответствии с изложенным выше, общее решение дифференциального уравнения имеет вид
. В соответствии с изложенным выше, общее решение дифференциального уравнения имеет вид  .
. , то результаты 3. справедливы и в случае комплексных чисел, однако при этом часть функций в фундаментальной системе решений окажется комплекснозначными. Чтобы от них перейти к функциям с действительными значениями, поступим аналогично пункту 2. и получим новую фундаментальную систему решений:
, то результаты 3. справедливы и в случае комплексных чисел, однако при этом часть функций в фундаментальной системе решений окажется комплекснозначными. Чтобы от них перейти к функциям с действительными значениями, поступим аналогично пункту 2. и получим новую фундаментальную систему решений: и
и  ,
,  .
. .
. , или
, или  . Корни этого уравнения:
. Корни этого уравнения:  ,
,  . В соответствии с результатами пункта 4, общим решением дифференциального уравнения будет функция
. В соответствии с результатами пункта 4, общим решением дифференциального уравнения будет функция  .
.
 ,
, фундаментальная система решений уравнения, которая ищется следующим образом:
фундаментальная система решений уравнения, которая ищется следующим образом:
 .
. и
и  , кратности 1 каждый, соответствуют два решения
, кратности 1 каждый, соответствуют два решения  и
и  .
. соответствуют
соответствуют  ,
,  ,
,  , …,
, …,  .
. решений
решений  ,
,  ,
,  ,…,
,…,  ,
,  .
. понимается линейный дифференциальный оператор вида
понимается линейный дифференциальный оператор вида , (1)
, (1) ,
,  определены и непрерывны на некотором интервале
определены и непрерывны на некотором интервале  , и рассматривается так называемое неоднородное уравнение
, и рассматривается так называемое неоднородное уравнение  , где
, где  также определена и непрерывна на
также определена и непрерывна на  . (2)
. (2) (3)
(3) общее решение однородного уравнения (3) (здесь
общее решение однородного уравнения (3) (здесь  фундаментальная система решений этого уравнения, а
фундаментальная система решений этого уравнения, а 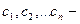 произвольные постоянные), а
произвольные постоянные), а  частное решение неоднородного уравнения (2) (т.е. одно из решений этого уравнения). Тогда функция
частное решение неоднородного уравнения (2) (т.е. одно из решений этого уравнения). Тогда функция (4)
(4) , эта функция зависит от
, эта функция зависит от  и
и  . При любых значениях этих постоянных функция (4) является решением уравнения (2):
. При любых значениях этих постоянных функция (4) является решением уравнения (2): 
 .
. зададим произвольные начальные условия
зададим произвольные начальные условия ,
,  , … ,
, … ,  и покажем, что постоянные
и покажем, что постоянные  . (5)
. (5) ,
,  , … ,
, … ,  . Определитель этой системы – это определитель Вронского
. Определитель этой системы – это определитель Вронского  , который отличен от 0 в силу линейной независимости функций
, который отличен от 0 в силу линейной независимости функций  . Значит, система (5) имеет единственное решение. ■
. Значит, система (5) имеет единственное решение. ■ частное решение уравнения
частное решение уравнения  , а
, а  частное решение уравнения
частное решение уравнения  . Тогда
. Тогда  частное решение уравнения
частное решение уравнения  .
. . ■
. ■ .
. (6)
(6)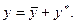
 , где
, где  многочлен степени
многочлен степени  является корнем характеристического уравнения для однородного уравнения (7) кратности
является корнем характеристического уравнения для однородного уравнения (7) кратности  ).
). , т.е.
, т.е.  .
. в виде
в виде  , где
, где  многочлен некоторой степени
многочлен некоторой степени  . Подставим такую функцию в уравнение (6), которое в данном случае (см. выше) имеет вид
. Подставим такую функцию в уравнение (6), которое в данном случае (см. выше) имеет вид  ,
, 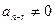 .
. . (8)
. (8)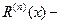 многочлен степени
многочлен степени  ,
,  многочлен степени
многочлен степени  , … ,
, … ,  многочлен степени
многочлен степени  . Тогда (
. Тогда ( 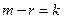 ,
,  .
. при
при  (так как эти коэффициенты «пропадут» при нахождении производных
(так как эти коэффициенты «пропадут» при нахождении производных 
 ,
, многочлен степени
многочлен степени  , где,
, где, 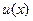
 , где
, где  – многочлен степени
– многочлен степени  . (9)
. (9) , получим тождественное равенство (на
, получим тождественное равенство (на  ) двух многочленов степени
) двух многочленов степени  уравнений с
уравнений с  кратность
кратность  .
. . Корни этого уравнения
. Корни этого уравнения  ,
, 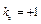 , и общее решение однородного уравнения
, и общее решение однородного уравнения  . Теперь ищем частное решение исходного уравнения:
. Теперь ищем частное решение исходного уравнения:  ,
,  ,
,  , и
, и  . Находим производные этой функции и подставляем в исходное уравнение (для удобства записи опуская символ *):
. Находим производные этой функции и подставляем в исходное уравнение (для удобства записи опуская символ *): 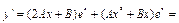
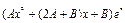 ;
;
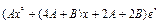 ; теперь
; теперь
 ;
; ;
;  .
.
 . Из этой системы
. Из этой системы  ;
;  ;
;  . В итоге,
. В итоге, 
 .
. , где
, где  и
и  многочлены степени
многочлены степени  ).
). , (10)
, (10) и
и  многочлены степени
многочлены степени  с неопределенными (действительными) коэффициентами
с неопределенными (действительными) коэффициентами  , а
, а 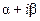 как корня характеристического уравнения для соответствующего однородного уравнения (7), или сколько раз
как корня характеристического уравнения для соответствующего однородного уравнения (7), или сколько раз  и
и  в обеих частях этого равенства (такие функции линейно независимы), получаем систему уравнений, из которой единственным образом находим коэффициенты многочленов
в обеих частях этого равенства (такие функции линейно независимы), получаем систему уравнений, из которой единственным образом находим коэффициенты многочленов 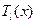 .
. .
. . Его характеристическое уравнение имеет вид
. Его характеристическое уравнение имеет вид  , или
, или  . Отсюда
. Отсюда  и
и  . Общее решение исходного уравнения:
. Общее решение исходного уравнения:  . Находим частное решение исходного уравнения:
. Находим частное решение исходного уравнения: 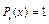 ,
, 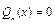 ,
,  ;
;  ,
,  ,
,  ; это число не является корнем характеристического уравнения, поэтому
; это число не является корнем характеристического уравнения, поэтому  и
и  . Отсюда (символ * для удобства записи опускаем)
. Отсюда (символ * для удобства записи опускаем)  ,
,  ,
,  . Подставляем в исходное уравнение:
. Подставляем в исходное уравнение:  ;
;  . Приравниваем коэффициенты при
. Приравниваем коэффициенты при  и
и  в левой и правой частях:
в левой и правой частях:  Отсюда
Отсюда  ,
,  и
и  .
. и
и  или только одной из них, в решении вида (10) должны быть обе эти функции.
или только одной из них, в решении вида (10) должны быть обе эти функции. (1)
(1) ,
,  (2)
(2) ,
,  (4)
(4) (11)
(11)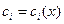 ,
,  .
. . Остальные
. Остальные  уравнения мы допишем наиболее удобным для нас способом. Имеем:
уравнения мы допишем наиболее удобным для нас способом. Имеем:

 (это 1-е уравнение)
(это 1-е уравнение)
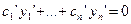 (это 2-е уравнение)
(это 2-е уравнение)
 (это
(это 
 , …, второе – на
, …, второе – на 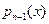 , первое – на
, первое – на  (все эти множители приведены в столбце слева), и все полученные новые равенства сложить. Собирая вместе члены с
(все эти множители приведены в столбце слева), и все полученные новые равенства сложить. Собирая вместе члены с  . (13)
. (13) ,
,  , …,
, …,  , и уравнение (13) приобретает вид
, и уравнение (13) приобретает вид . (14)
. (14) :
: . (15)
. (15) . Ее легко запомнить: коэффициентами являются – в 1-м уравнении
. Ее легко запомнить: коэффициентами являются – в 1-м уравнении  , в 3-м
, в 3-м  и т. д.; правые части, кроме последней (
и т. д.; правые части, кроме последней (  ой), равны 0, а последняя правая часть равна
ой), равны 0, а последняя правая часть равна  , который отличен от 0 во всех точках интервала
, который отличен от 0 во всех точках интервала  ,
,  , …,
, …,  .
. .
. . Характеристическое уравнение
. Характеристическое уравнение  имеет корни
имеет корни  ,
,  , и общее решение имеет вид
, и общее решение имеет вид  . Теперь ищем частное решение
. Теперь ищем частное решение  исходного уравнения по той же формуле, считая, что в ней
исходного уравнения по той же формуле, считая, что в ней  ,
, 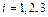 . Система (15) выглядит так:
. Система (15) выглядит так: . Складывая 2-е и 3-е уравнения, имеем:
. Складывая 2-е и 3-е уравнения, имеем:  ;
;  .
.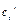 во 2-е уравнение:
во 2-е уравнение: 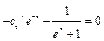 ;
;  . Подставим
. Подставим  и
и  . Теперь находим сами коэффициенты
. Теперь находим сами коэффициенты 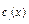 (произвольные постоянные не пишем, так как находим лишь одно частное решение неоднородного уравнения):
(произвольные постоянные не пишем, так как находим лишь одно частное решение неоднородного уравнения):
 ;
;
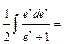


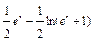 ;
;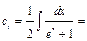


 .
. и
и .
.