 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Приведение квадратной матрицы к диагональному виду
Наиболее простой вид принимает матрица
Пример 56.В некотором базиселинейный оператор задан матрицей Решение Матрица имеет диагональный вид в базисе из собственных векторов, поэтому найдем собственные векторы. Характеристическое уравнение:
Если пусть Если Пусть Таким образом, матрица
Матрица Правило построения матрицы 1. Найти все собственные значения матрицы 2. Для каждого собственного числа 3. Построить матрицу 4. Если полученная матрица Пример 57.Найти матрицу Решение Вычислим определитель матрицы
Собственные числа матрицы Построим фундаментальные системы решений систем уравнений ФСР первой системы состоит из одного решения Следовательно, матрица Полученная матрица не является квадратной, поэтому матрица Пример 58. Привести к диагональному виду с помощью ортогональной матрицы симметрическую матрицу Решение Характеристическое уравнение матрицы Матрица ФСР системы уравнений Матрица
После ортогонализации и нормирования столбцов этой матрицы получим ортогональную матрицу Матрица, обратная к т.е. Нетрудно проверить, что Квадратичные формы Переход от системы Определение. Квадратичной формой Квадратичную форму можно записать в виде
где Пример 59.Написать матрицу квадратичной формы
Решение Обозначим коэффициенты при произведении
Теперь матрица А квадратичной формы
Пример 60. Дана квадратичная форма
Записать ее в матричном виде. Решение Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, а другие элементы – половинам соответствующих коэффициентов квадратичной формы. Получили:
Две квадратичные формы называются эквивалентными, если одна из них переводится в другую посредством невырожденного линейного преобразования. Если в квадратичной форме Пример 61. Дана квадратичная форма Решение Матрица данной квадратичной формы Следовательно, по (12) матрица искомой квадратичной формы
Определение. Каноническим видом данной квадратичной формы называется эквивалентная ей форма, не содержащая произведений неизвестных. Каждую квадратичную форму можно привести к каноническому виду с помощью линейного преобразования неизвестных Пример 62. Привести к каноническому виду квадратичную форму
Решение Сгруппируем все члены, содержащие неизвестное
Теперь перейдем от неизвестных
В результате этого перехода получили канонический вид данной квадратичной формы:
Если
Следующие утверждения равносильны: 1) Квадратичная форма 2) Собственные значения матрицы А положительны. 3) Угловые миноры матрицы А положительны.
А также равносильны следующие утверждения: 1) Квадратичная форма 2) Собственные значения матрицы А отрицательны. 3) Все угловые миноры матрицы А нечетного порядка отрицательны, а все угловые миноры четного порядка положительны. |



 линейного оператора
линейного оператора  линейно независимых собственных векторов
линейно независимых собственных векторов  с собственными значениями, соответственно равными
с собственными значениями, соответственно равными  . Векторы
. Векторы 
 откуда
откуда  если
если  и
и  если
если  Таким образом, матрица оператора
Таким образом, матрица оператора  . (10)
. (10)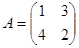 . В действительном линейном пространстве найти базис, в котором матрица этого оператора имеет диагональный вид.
. В действительном линейном пространстве найти базис, в котором матрица этого оператора имеет диагональный вид. его корни
его корни 
 то
то 
 тогда
тогда  , собственный вектор
, собственный вектор  .
. то
то 
 , собственный вектор
, собственный вектор  .
.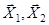 имеет вид:
имеет вид:  .
. , что
, что  - диагональная матрица. Матрица
- диагональная матрица. Матрица  имеется базис, состоящий из собственных векторов матрицы
имеется базис, состоящий из собственных векторов матрицы 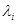 найти фундаментальную систему решений однородной системы линейных уравнений
найти фундаментальную систему решений однородной системы линейных уравнений к диагональному виду. Найти матрицу
к диагональному виду. Найти матрицу  .
. :
:
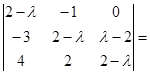

 .
. и
и 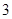 .
.

 , а второй – из одного решения
, а второй – из одного решения  .
. .
. .
.


 .
.
 состоит из двух векторов:
состоит из двух векторов:  ,
,  , а системы уравнений
, а системы уравнений  - из одного вектора
- из одного вектора  .
. .
. .
. , совпадает с
, совпадает с  ,
, .
. .
. к системе
к системе  по формуле
по формуле  где
где  - квадратная матрица порядка
- квадратная матрица порядка  от
от  , (11)
, (11) - симметрическая матрица порядка
- симметрическая матрица порядка  .
.
 через
через  причем
причем 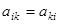 . Член
. Член  запишем в виде
запишем в виде  . Тогда квадратичную форму можно записать в виде
. Тогда квадратичную форму можно записать в виде .
. имеет вид:
имеет вид: .
. .
.
 с матрицей
с матрицей  . (12)
. (12)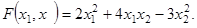 Найти квадратичную форму
Найти квадратичную форму  , полученную из данной линейным преобразованием
, полученную из данной линейным преобразованием 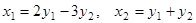 .
. , а матрица линейного преобразования
, а матрица линейного преобразования  .
. .
. с ортогональной матрицей
с ортогональной матрицей  .
. .
. , и дополним их до полного квадрата:
, и дополним их до полного квадрата: В дальнейшем полный квадрат, содержащий неизвестное
В дальнейшем полный квадрат, содержащий неизвестное  , и дополним их до полного квадрата:
, и дополним их до полного квадрата:
 к неизвестным
к неизвестным  по формулам:
по формулам:
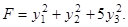
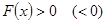 для всех
для всех  , то квадратичная форма
, то квадратичная форма