 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Собственные векторы и собственные значения линейного оператора
Линейные операторы Определение.Пусть Записывают: Говорят: «Оператор Принято называть Оператор 1. 2. Если пространства Пример 52.Проверить линейность оператора
Выберем в пространстве Запишем разложение произвольного вектора В силу линейности оператора
Так как
Тогда С другой стороны, вектор
Так как любой вектор можно разложить по базису, причем единственным образом, получаем равенство правых частей в (5) и (6). Отсюда Матрица Утверждение. Каждому линейному оператору соответствует матрица в данном базисе. Собственные векторы и собственные значения линейного оператора Определение. Пусть R – заданное
Число Собственный вектор под действием линейного оператора Равенство (7) можно представить в матричной форме:
где вектор
Перепишем систему так, чтобы в правых частях были нули:
Или в матричном виде Полученная однородная система всегда имеет нулевое решение. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы был равен нулю:
Определитель системы
По основной теореме алгебры, уравнение
Характеристический многочлен линейного оператора не зависти от выбора базиса.
Пример 53. Найти собственные числа и собственные векторы линейного оператора Решение Составим характеристическое уравнение, используя формулу (9):
Вычислим полученный определитель (понижением порядка):
Найдем собственные векторы.
Если
Пусть Составим собственный вектор Если Пусть Составим собственный вектор Если Пусть Составим собственный вектор Пример 54 . Найти собственные числа матрицы Решение Составим характеристическое уравнение матрицы,
Пример 55. Найти собственные векторы матрицы Решение Впримере выше были найдены собственные числа матрицы 1)Если Решим данную систему методом Гаусса:
Пусть Получим собственный вектор 2) Если Решаем систему:
Получим собственный вектор |



 и
и  два линейных пространства. Если дано правило, по которому каждому элементу
два линейных пространства. Если дано правило, по которому каждому элементу  ставится в соответствие элемент
ставится в соответствие элемент  ,
,  , то говорят, что задан оператор (отображение, закон), действующий из пространства
, то говорят, что задан оператор (отображение, закон), действующий из пространства 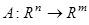 или
или 
 переводит вектор
переводит вектор  в вектор
в вектор 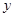 ».
». - свойство аддитивности оператора;
- свойство аддитивности оператора; - свойство однородности оператора.
- свойство однородности оператора.
 по данному базису:
по данному базису: 
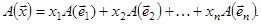
 также вектор из
также вектор из 

 (5)
(5) , имеющий в том же базисе
, имеющий в том же базисе 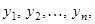 можно записать так:
можно записать так: (6)
(6)
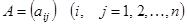 называется матрицей оператора
называется матрицей оператора  матрицы
матрицы  - мерное линейное (векторное) пространство. Ненулевой вектор
- мерное линейное (векторное) пространство. Ненулевой вектор  R называется собственным вектором линейного оператора
R называется собственным вектором линейного оператора  , что выполняется равенство:
, что выполняется равенство: (7)
(7) .
. ,
,
 (8)
(8)
 (9)
(9) является многочленом
является многочленом  .
.




 - собственные числа (значения) линейного оператора (собственные числа матрицы оператора).
- собственные числа (значения) линейного оператора (собственные числа матрицы оператора). , то для определения координат собственного вектора составим и решим соответствующую систему уравнений:
, то для определения координат собственного вектора составим и решим соответствующую систему уравнений:


 (свободная переменная), тогда
(свободная переменная), тогда  ,
, 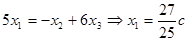 .
. .
. , то
, то  .
. 
 , тогда
, тогда  и
и  .
. .
. , то
, то  .
. , тогда
, тогда  и
и  .
. .
. .
.
 - характеристическое уравнение оператора (матрицы)
- характеристическое уравнение оператора (матрицы)  . Следовательно, матрица
. Следовательно, матрица  .
.

 , то для определения координат собственного вектора получаем систему уравнений
, то для определения координат собственного вектора получаем систему уравнений 
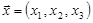 , которая имеет вид:
, которая имеет вид: 
 ~
~  ~
~  ~
~ 

 и
и  .
. .
. , тогда
, тогда  .
. ~
~  ~
~ 
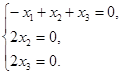 Находим
Находим 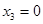 ,
, 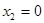 и
и 
 .
.