 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Разновидности математических моделей и их использование
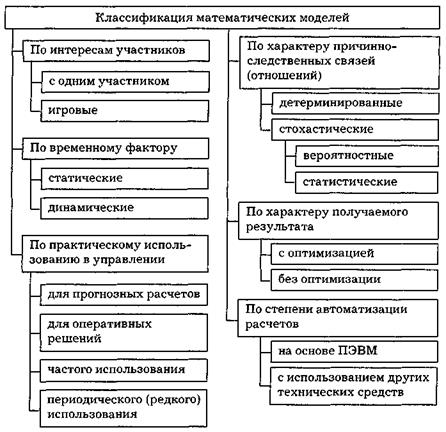
Моделирование как метод разработки управленческого решения используется с середины XX в. Первые модели базировались на нормативных теориях и назывались нормативными. В них описывается стратегия поведения при выработке решения, ориентирующая на заданный критерий. Примером нормативных моделей являются: • модели принятия статистических решений с использованием теории вероятности и математической статистики; • инновационные игры как вариант нормативной модели поведения в условиях конфликта, наличия разноречивых мнений по проблемам нововведения; • модели разработки решений на основе теории массового обслуживания, содержащие нормативные критерии при решении конкретных задач. Содержание процесса разработки решения в этом случае сводится к поиску оптимального решения, в наибольшей степени соответствующего заданному критерию. Достигается это сопоставлением альтернатив решений, рассчитанных для конкретных состояний переменных факторов (условий внешней среды). Однако нормативные модели не учитывают при принятии решений реального поведения человека, за которым остается выбор окончательного варианта. Этот "недостаток" в определенной мере компенсируют дескриптивные модели разработки решений, основанные на теории полезности, теории риска. В настоящее время выделяются три основных подхода к построению моделей процесса разработки решений (математическому моделированию), основанных: 1) на теории статистических решений; 2) на теории полезности; 3) на теории игр. Наиболее разработаны модели на основе теории статистических решений. В них считаются заданными: • возможное распределение изучаемого случайного процесса; • пространство возможных окончательных решений; • стоимость вариантов решений; • функция возможного убытка для каждого решения, соответствующего определенному состоянию внешней среды. В общем виде можно констатировать, что решения принимаются, исходя из максимума прибыли или минимума потерь В связи с этим вводится понятие риска, по величине которого судят о ценности решения. В этой теории рассматривается ряд возможных критериев оптимальности принимаемых решений. Так, решение, минимизирующее максимальный риск (байесовское решение), описывается как минимаксное решение. Статистическая теория решения применяется при выборе решений в условиях неопределенности внешней среды. Второе направление математического моделирования связано с использованием теории полезности, основанной на индивидуальных предпочтениях, субъективной оценке вероятностей наступления событий внешней среды. Третье направление моделей разработки решений основано на использовании теории игр. Данная теория применяется в условиях конфликтных ситуаций либо при принятии коллективных (совместных) решений. Основополагающим является выбор отправной точки (гарантирующего решения), с которой начинается совместная выработка лучшего решения. Основной принцип этой теории — минимакс. Схема теории игр описывает принципы принятия решений для широкого класса практических ситуаций инновационного характера. Игра возможна с любым числом участников и различной степенью их информированности. Формализации подвергаются лишь правила игры, а не поведение игроков. Приведенные теории и подходы к моделированию процесса разработки решений отражают определенные его стороны: статистическая теория решений — неопределенность среды, выбор, риск; теория игр — некоторые характеристики поведения человека в условиях взаимодействия с другими людьми и со средой; теория полезности — психологические представления о потребностях человека и его мотивации. Разновидностью .разработки решений являются эвристические модели. Впервые авторы Герберт А. Саймон и Д. Ньюэл использовали термин "эвристический" (греческое "эурискеин" — делаю открытие) для характеристики особого подхода к решению задач и выбору решений. Основу эвристических моделей составляют логика и здравый смысл, основанные на имеющемся опыте. Такие модели используются в ситуациях, когда невозможно применение формальных аналитических методов. Сущность эвристических методов состоит в преобразовании одной сложной задачи в совокупность простых, поддающихся изучению математическими способами. Эвристическими моделями не решаются задачи оптимизации решений, но оценивается относительная пригодность конкретных стратегий с определенными ограничениями. На основе построения модели логических связей в ходе рассуждений ЛПР может решаться широкий класс задач. Эвристические модели используются при выборе решений для разрешения ситуаций кратковременных и повторяющихся, а также сложных и повторяющихся без надежды на использование при этом математического аппарата. Практическое применение эвристического подхода к моделированию процесса разработки и принятия управленческих решений предполагает наличие у ЛПР познавательных способностей и склонностей к обобщениям и выводам. Принятие решений на психологическом уровне не является изолированным процессом. Оно включено в контекст реальной деятельности человека. При построении моделей принятия решений важно знать, как развертываются процессы, предшествующие ему и следующие за ним. Необходимо исследовать внешнюю и внутреннюю среду, включая поиск, выделение, классификацию и обобщение информации о среде, сформировать альтернативы и сделать выбор. Существует большое разнообразие математических моделей, отражающих реальные процессы, протекающие в экономической жизни предприятия. Их можно классифицировать по разным признакам (рис. 4.3).
Рис. 3.Классификация математических моделей
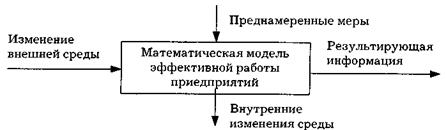
Следует отметить, что вопрос о классификации моделей в теории принятия решений продолжает оставаться спорным. Краткая характеристика и направление использования конкретных моделей сводятся к следующему. В моделях могут отражаться интересы участников экономического процесса. Если они (интересы) одинаковы (хотя бы при нескольких действующих лицах), то модели называются моделями с одним участником; если интересы участников расходятся __то игровыми моделями. В рыночной экономике игровые модели имеют значительное распространение. Если в моделях отсутствует фактор времени, рассматривается процесс в конкретный момент или на фиксированном отрезке времени, то такие модели называются статическими. Область применения этих моделей ограничивается краткосрочным прогнозированием (например, статическая модель межотраслевого баланса). В динамических моделях появляется возможность отразить во времени процесс функционирования и развития объекта управления. Фактор времени присутствует в явном виде (например, долгосрочное прогнозирование развития спроса с использованием метода экстраполяции — в этом случае сложившаяся тенденция развития явления в прошлом времени переносится на будущее). В детерминированных моделях каждому значению фактора (набору исходных данных) строго соответствует единственное значение результата, т. е. существует функциональная связь. Частным случаем этого класса моделей являются квазирегулярные модели. Это модели динамики средних описывают процесс на основе средневзвешенных значений параметров модели. Они достаточно широко применяются в соци- ально-экономических исследованиях. Их особенность состоит в том, что каждому значению аргумента соответствует определенная величина функции, т. е. посредством модели можно получить вполне определенный результат (например, зависимость объема спроса от величины покупательных фондов населения). Стохастические модели характеризуются более полным отражением действительности, они ближе к реальным процессам, где отсутствует жесткая детерминация. Например, на одинаковом оборудовании может быть разная производительность труда. Данный класс моделей носит вероятностный характер, так как они подсказывают результат с некоторой уверенностью. В данном классе моделей выделяют две разновидности: вероятностные и статистические модели. Вероятностные модели используют вероятностные значения параметров процесса. Однако математическая структура вероятностных моделей строго детерминирована. Для каждого набора исходных данных в моделях определяется единственное распределение вероятностей случайных событий в рассматриваемом процессе. Для реализации вероятностных моделей необходимо, чтобы каждому состоянию отдельного элемента системы соответствовала вероятность его попадания в это состояние. Для отображения этой моделью динамики функционирования предприятия необходимо разделить траекторию возможных состояний каждого элемента системы на определенное (дискретное) число состояний и определить вероятности перехода этого элемента из одного состояния в другое с учетом взаимного влияния элементов. В статистических моделях каждому набору исходных данных соответствует в модели какой-либо случайный результат из множества возможных. Таким образом, каждое решение предлагает одну случайную реализацию результатов моделируемого процесса. Одним из эффективных приемов исследования экономических систем, используемых в процессе принятия управленческих решений, является динамическое моделирование.Оно представляет собой создание условной математической модели деятельности предприятия и ее эффективности, по которой прослеживаются изменения, происходящие в управляемом объекте под влиянием мер, преднамеренно предпринимаемых в процессе управления, а также под реальным воздействием внутренней и внешней среды. Схема такова (рис. 4).
Рис. 4.Схема динамического моделирования Технология динамического моделирования включает: 1) определение проблемы, которая должна быть решена в управляемой системе; 2) установление факторов, которые могут проявить себя при решении проблемы, т. е. выявление причинно-следственных связей и их влияния на результаты работы предприятия; 3) определение количественного выражения этих связей. Математическая модель динамического моделирования представляет собой систему этих связей и их количественное выражение. Создание такой модели — сложная и трудоемкая работа. Представляется оправданным использование типовых моделей с последующим их приспособлением к нуждам конкретного предприятия. Необходимость использования динамического моделирования вызвана следующими причинами: 1) суждения руководителей о решениях, последствиях, которые они могут вызвать, в значительной мере субъективны; 2) проведение экспериментов по принимаемым решениям для их проверки — в экономическом и социальном плане сложная задача; 3)ряд обстоятельств, связанных с реализацией решений, трудно учесть логическим путем; 4) действие внешней среды трудно предвидеть; 5) положительный эффект на одном участке предприятия может отражаться негативно на других участках объекта управления. Особенность динамического моделирования состоит в том, что, какими бы ни были первоначальное состояние и первоначальное решение, все последующие решения должны исходить из состояния, полученного в результате предыдущего решения.
где
Многошаговость отражает реальное протекание процесса принятия решения либо искусственное расчленение процесса принятия однократного решения на отдельные этапы и шаги. Сетевое моделированиевесьма эффективно на всех этапах разработки решений: в ходе поиска решений, выбора оптимального варианта и контроля за реализацией решений. Положительными признаками сетевого моделирования являются детализация проблемы, конкретизация ответственности, улучшение оперативного руководства и контроля, рациональное использование ресурсов и времени (подробно изложено в гл. 8). В системе моделирования хозяйственных явлений часто используются матричные модели,в которых совмещаются математические средства с наглядным отображением взаимосвязи разделов плана (или отчета) предприятия. В матричной модели ресурсы (производственные мощности, трудовые, материальные ресурсы, технологические нормативы) выражаются в сочетании с объемами производства, затратами (трудовыми, финансовыми, материальными) за определенный период, степенью использования ресурсов по их видам. Матричная модель эффективно используется для выявления взаимосвязей между различными сторонами деятельности предприятий, возникающих в результате выполнения какого-либо управленческого решения. По существу матричная модель представляет собой один из видов балансовых моделей. После создания математической модели производят пробные расчеты (в том числе с помощью вычислительных машин) для проверки степени близости модели к реальной действительности. По результатам сравнения осуществляется корректирование: либо модели, если она не соответствует действительности, либо меняются взаимоотношения в организации и правила принятия управленческих решений, если модель выявила их несовершенство. Одной из разновидностей являются имитационные модели,рассчитанные на использование ЭВМ, которые рассматриваются ниже. |




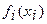 — прирост выпуска по
— прирост выпуска по  -му направлению при выделении
-му направлению при выделении  ресурсов;
ресурсов; — суммарный прирост выпуска по направлениям от первого до
— суммарный прирост выпуска по направлениям от первого до