ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Ситуационная (практическая) задача № 2 12
Имеются поквартальные данные по товарообороту некоторой компании в 1999-2008 гг.
Требуется: 1. Проверить гипотезу о наличии тренда во временном ряде. 2. Рассчитать коэффициенты автокорреляции. Проверить наличие сезонных колебаний во временном ряде. 3. Оценить параметры линейной трендовой модели, проверить статистическую значимость соответствующего уравнения регрессии с надежностью 0,99. 4. Дать точечный и интервальный прогноз товарооборота компании на 2011 год с надежностью 0,99. Решение: 1. Проверим гипотезу о наличии тренда во временном ряде. Значение критерия рассчитаем по формуле:
где
Критическим значением критерия Стьюдента при уровне значимости 2. Рассчитаем коэффициенты автокорреляции. Коэффициент автокорреляции уровней ряда 1-го порядка:
где Коэффициент автокорреляции уровней ряда 2-го порядка:
Аналогично можно найти коэффициенты автокорреляции уровней ряда n-го порядка. Однако для обеспечения статистической достоверности коэффициентов автокорреляции воспользуемся правилом: max лаг £ n/4, то есть в нашем случае максимальный лаг будет равен 3. Расчет коэффициента автокорреляции 1-го порядка
Расчет коэффициента автокорреляции 2-го порядка
Расчет коэффициента автокорреляции 3-го порядка
По значениям коэффициентов автокорреляции можно сделать вывод о наличии сезонных колебаний. 3. Оценим параметры линейной трендовой модели. В соответствии с методом наименьших квадратов оценки параметров уравнения линейного тренда
Уравнение тренда будет иметь вид:
Проверим статистическую значимость уравнения регрессии с надежностью 0,99. Найдем коэффициент детерминации:
Вычислим коэффициент детерминации:
Оценим качество уравнения регрессии с помощью F-критерия Фишера. Проверим гипотезу Н0 о статистической незначимости уравнения регрессии:
Критическое значение критерия 4. Дадим точечный и интервальный прогноз товарооборота компании на 2011 год с надежностью 0,99. Точечный прогноз:
Интервальный прогноз:
Тестовыезадания Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению. 1. С помощью какого метода можно найти оценки параметра уравнения линейной регрессии: a) метода наименьших квадратов; b) корреляционно-регрессионного анализа; c) дисперсионного анализа; d) метода серий.
2. Уравнение регрессии, описывающее зависимость удельных постоянных расходов от объема выпускаемой продукции имеет вид: a) -0,9; b) 0,75; c) 1,5; d) -0,75.
3. Линейный коэффициент парной корреляции для величин X и Y равен 0,8. Чему равен коэффициент детерминации для линейного уравнения парной регрессии, построенного по этой выборке? a) 0,64; b) 0,894; c) 0,2; d) 0,4.
4. По 30 наблюдениям построено уравнение регрессии a) b) c) d)
5. По формуле вычисляется a) статистика χ2 для проверки наличия мультиколлинеарности в модели регрессии; b) вектор оценок коэффициентов для уравнения множественной регрессии; c) критерий для проверки адекватности модели; d) прогнозное значение исследуемого показателя.
6. С помощью какого критерия проверяют наличие автокорреляции остатков? a) Дарбина-Уотсона; b) Фишера; c) Голдфельда-Кванта; d) Стьюдента.
7. Следствием гетероскедастичности является a) несостоятельность оценок параметров уравнения, полученных по МНК; b) смещенность оценок параметров уравнения, полученных по МНК; c) неприменимость статистических тестов; d) ненадежность оценок параметров уравнения, полученных по МНК.
8. Какая из составляющих временного ряда описывает конъюнктурные факторы, формирующие изменения анализируемого признака, обусловленные воздействием долговременных циклов экономической, демографической или солнечной активности? a) тренд; b) сезонная составляющая; c) циклическая составляющая; d) случайная составляющая.
9. Какая из представленных моделей временного ряда является моделью тренда? a) yt*= at+b+ε; b) yt*= a0+a1t+a2cos(kt)+a3sin(kt)+ε; с) yt*= ayt-1+b+ε; d) yt*= a0+a1t+a2t2+b1δ1+ b2δ2+ ε.
10. Для каких видов систем параметры отдельных эконометрических уравнений могут быть найдены с помощью обычного МНК? a) система нормальных уравнений; b) система независимых уравнений; c) система рекурсивных уравнений; d) система взаимозависимых уравнений. 12 |



 ,
,
 ,
, 
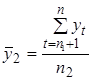 ,
, 





 ,
, 

 ,
, 

 и числе степеней свободы
и числе степеней свободы  является
является  . Так как
. Так как 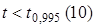 , то гипотезу об отсутствии тренда принимаем, то есть тренд отсутствует.
, то гипотезу об отсутствии тренда принимаем, то есть тренд отсутствует. ,
,





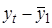





















 вычислим по формулам:
вычислим по формулам: ,
, 



 ,
, 








 . Так как критическое значение больше фактического, то гипотезу Н0 отклоняем, то есть данное уравнение регрессии не является статистически значимым.
. Так как критическое значение больше фактического, то гипотезу Н0 отклоняем, то есть данное уравнение регрессии не является статистически значимым.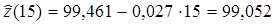 млн. руб.
млн. руб.
 ,
, 


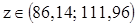
 . Чему может быть равен линейный коэффициент парной корреляции?
. Чему может быть равен линейный коэффициент парной корреляции? . Каким квантилем нужно воспользоваться при проверке статистической значимости коэффициентов частной корреляции для этого уравнения?
. Каким квантилем нужно воспользоваться при проверке статистической значимости коэффициентов частной корреляции для этого уравнения?