 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Ситуационная (практическая) задача № 1 12
Предполагается, что объем предложения Y некоторого блага для функционирующей в условиях конкуренции фирмы линейно зависит от цены этого блага X1 и заработной платы X2 сотрудников фирмы, производящих данное благо. Статистические данные за 18 месяцев собраны в следующую таблицу:
Требуется: 1. Построить корреляционное поле между объемом предложения блага и его ценой. Выдвинуть гипотезу о тесноте и виде зависимости между указанными показателями. 2. Оценить тесноту линейной связи между объемом предложения блага и его ценой с надежностью 0,9. 3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости объема предложения блага от его цены. 4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,9 и построить для них доверительные интервалы. 5. Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,9. 6. Дать точечный и интервальный прогноз с надежностью 0,9 объема предложения, если цена блага составит 30 руб. 7. Рассчитать коэффициенты линейного уравнения множественной регрессии и пояснить экономический смысл его параметров. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы. 9. Найти коэффициенты парной и частной корреляции. Проанализировать их. 10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации. 11. С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9. 12. Дать точечный и интервальный прогноз с надежностью 0,9 объема предложения блага для фирмы, если цена блага составит 30 руб., а заработная плата сотрудников фирмы равна 11 тыс. руб. 13. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты. Решение: 1. Построим корреляционное поле между объемом предложения блага и его ценой:
По виду корреляционного поля можно предположить, что между объемом предложения блага Y и его ценой X1 существует тесная прямая линейная зависимость 2. Оценим тесноту линейной связи между объемом предложения блага и его ценой, для этого вычислим коэффициент линейной корреляции:
Полученное значение коэффициента корреляции говорит о сильной прямой линейной связи между объемом предложения блага и его ценой. Для проверки значимости найденного коэффициента корреляции вычислим расчетное значение t-критерия:
Найдем табличное значение t-критерия: 3. Рассчитаем коэффициенты линейного уравнения регрессии
Получили линейное уравнение регрессии для зависимости Y(Х1):
4. Проверим статистическую значимость параметров уравнения регрессии с надежностью 0,9. Выдвинем гипотезу Н0:
Рассчитаем значение критерия при
Так как оба расчетных значения t-критерия по модулю больше табличного значения Построим доверительный интервал для коэффициента
Построим доверительный интервал для коэффициента
5. Рассчитаем коэффициент детерминации. Так как регрессия парная, то
Оценим качество уравнения регрессии с помощью F-критерия Фишера. Проверим гипотезу Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Рассчитаем фактическое значение F-статистики Фишера. Так как регрессия парная, то фактическое значение найдем по формуле:
Определим табличное значение критерия: при 6. Дадим точечный прогноз объема предложения, если цена блага составит 30 руб.:
Составим интервальный прогноз объема предложения с надежностью 0,9:
7. Рассчитаем коэффициенты линейного уравнения множественной регрессии. В соответствии с методом наименьших квадратов оценки параметров множественной линейной регрессионной модели
где Х – матрица размером 18х3, первый столбец которой является единичным, а два других представляют собой значения
Y – столбец значений
Получили уравнение множественной регрессии:
Поясним экономический смысл его параметров. Свободный коэффициент уравнения множественной регрессии отражает объем предложения блага при его нулевой цене и нулевой заработной плате (в данном случае интерпретация свободного коэффициента не имеет физического смысла). Из уравнения множественной регрессии видно, что при неизменной заработной плате увеличение цены блага на 1 руб. предположительно может увеличить объем предложения блага на 1,103 тыс. ед., а при неизменной цене блага увеличение заработной платы на 1 тыс. руб. предположительно может привести к росту объема предложения блага на 3,115 тыс. ед. 8. Проанализируем статистическую значимость коэффициентов множественного уравнения с надежностью 0,9. Расчетное значение t-критерия вычислим по формуле:
где
Найдем табличное значение критерия для 9. Найдем коэффициенты парной корреляции. Коэффициент корреляции между объемом предложения блага и его ценой найден в п. 2:
Значение коэффициента корреляции говорит о наличии между объемом предложения блага и его ценой сильной прямой связи. Аналогично найдем коэффициент парной корреляции между объемом предложения блага и заработной платой:
Значение коэффициента корреляции говорит о наличии между объемом предложения блага и заработной платой сильной прямой связи. Найдем общий коэффициент детерминации:
Рассчитаем фактическое значение при
Найдем частные коэффициенты корреляции:
Таким образом, более тесная связь наблюдается между объемом предложения блага и его ценой. 10. Общий коэффициент детерминации был найден в предыдущем пункте:
Найдем скорректированный коэффициент детерминации:
Значение скорректированного коэффициента детерминации близко к значению общего коэффициента детерминации. 11. Оценим адекватность уравнения регрессии с помощью F-теста. Проверим гипотезу Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Так как регрессия множественная (
Найдем табличное значение критерия: при 12. Дадим точечный и интервальный прогноз с надежностью 0,9 объема предложения блага для фирмы, если цена блага составит 30 руб., а заработная плата сотрудников фирмы равна 11 тыс. руб.:
Сделаем интервальный прогноз с надежностью 0,99:
где
13. Проверим построенное уравнение на наличие мультиколлинеарности по критерию Стьюдента. Для определения мультиколлинеарности найдем коэффициент корреляции
Проверим, что этот коэффициент незначимо отличается от нуля:
Расчетное значение критерия по модулю больше табличного, поэтому можно считать, что переменные Для проверки по критерию «хи-квадрат» χ2 на уровне значимости 0,01 найдем определитель матрицы коэффициентов парной корреляции:
Вычислим χ2-критерий:
Найдем табличное значение χ2 при Таким образом, и тот и другой критерий показали наличие мультиколлинеарности. 12 |




 .
.
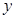







 ,
,  . Так как
. Так как  , то с надежностью 0,9 можно утверждать, что полученный коэффициент корреляции является статистически значимым.
, то с надежностью 0,9 можно утверждать, что полученный коэффициент корреляции является статистически значимым. ,
, 
 ,
, 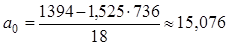

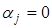 о незначимом отклонении от нуля каждого отдельного параметра модели. Эта гипотеза отклоняется при
о незначимом отклонении от нуля каждого отдельного параметра модели. Эта гипотеза отклоняется при  .
. ,
,




 ,
,
 , то параметры уравнения регрессии являются статистически значимыми.
, то параметры уравнения регрессии являются статистически значимыми. :
:



 :
:






 ,
, 
 . Так как табличное значение меньше фактического
. Так как табличное значение меньше фактического  , то гипотезу Н0 отклоняем, то есть данное уравнение регрессии является статистически значимым.
, то гипотезу Н0 отклоняем, то есть данное уравнение регрессии является статистически значимым. тыс. ед.
тыс. ед. ,
,




 вычислим по формуле:
вычислим по формуле: ,
,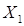 и
и  :
:


 .
.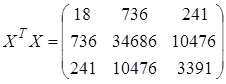



 ,
,  ,
, 
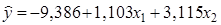
 ,
,
 - диагональный элемент матрицы
- диагональный элемент матрицы  .
.
 ,
, ,
,
 ,
,  ,
,  ,
, :
:  . Так как все расчетные значения t-критерия больше табличного значения, то параметры все параметры уравнения множественной регрессии являются статистически значимыми.
. Так как все расчетные значения t-критерия больше табличного значения, то параметры все параметры уравнения множественной регрессии являются статистически значимыми.




 :
:






 ), то фактическое значение F-статистики Фишера вычислим по формуле:
), то фактическое значение F-статистики Фишера вычислим по формуле:

 ,
, 
 . Так как
. Так как  , то есть табличное значение критерия меньше расчетного
, то есть табличное значение критерия меньше расчетного  тыс. ед.
тыс. ед.
 ,
, - вектор независимых переменных, для которого определяется интервал;
- вектор независимых переменных, для которого определяется интервал; 




 :
:










 коррелирует между собой и, следовательно, мультиколлинеарность присутствует.
коррелирует между собой и, следовательно, мультиколлинеарность присутствует.

 и
и  :
:  . Так как
. Так как  , то в соответствии с критерием Пирсона мультиколлинеарность присутствует.
, то в соответствии с критерием Пирсона мультиколлинеарность присутствует.