 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Релятивистское сложение скоростей 12
5.9. Показать, что формула сложения скоростей релятивистских частиц переходит в соответствующую формулу классической механики при υ <<c. 5.10.Две релятивистские частицы движутся в лабораторной системе отсчета со скоростями υ1=0,6 с и υ2=0,9 с вдоль одной прямой. Определить их относительную скорость u21 в двух случаях: 1) частицы движутся в одном направлении; 2) частицы движутся в противоположных направлениях. 5.11. В лабораторной системе отсчета удаляются друг от друга две частицы с одинаковыми по модулю скоростями. Их относительная скорость u в той же системе отсчета равна 0,5 с. Определить скорости частиц. 5.12. Ион, вылетев из ускорителя, испустил фотон в направлении своего движения. Определить скорость фотона относительно ускорителя, если скорость υ иона относительно ускорителя равна 0,8 с. 5.13. Ускоритель сообщил радиоактивному ядру скорость υ1= =0,4 с. В момент вылета из ускорителя ядро выбросило в направлении своего движения β-частицу со скоростью υ2=0,75 с относительно ускорителя. Найти скорость u21 частицы относительно ядра. 5.14.Два ускорителя выбрасывают навстречу друг другу частицы со скоростями |υ|=0,9 с. Определить относительную скорость и21 сближения частиц в системе отсчета, движущейся вместе с одной из частиц. Релятивистская масса и релятивистский импульс 5.15. Частица движется со скоростью υ=0,5 с. Во сколько раз релятивистская масса частицы больше массы покоя? 5.16. С какой скоростью υ движется частица, если ее релятивистская масса в три раза больше массы покоя? 5.17. Отношение заряда движущегося электрона к его массе, определенное из опыта, равно 0,88×1011 Кл/кг. Определить релятивистскую массу т электрона и его скорость υ. 5.18.На сколько процентов релятивистская масса частицы больше массы покоя при скорости υ=30 Мм/с? 5.19.Показать, что выражение релятивистского импульса переходит в соответствующее выражение импульса в классической механике при υ<<c. 5.20.Электрон движется со скоростью υ=0,6 с. Определить релятивистский импульс р электрона. 5.21.Импульс р релятивистской частицы равен т0с (т0 — масса покоя). Определить скорость υ частицы (в долях скорости света). 5.22. В лабораторной системе отсчета одна из двух одинаковых частиц покоится, другая движется со скоростью υ=0,8 с по направлению к покоящейся частице. Определить: 1) релятивистскую массу движущейся частицы в лабораторной системе отсчета; 2) скорость частиц в системе отсчета, связанной с центром инерции системы; 3) релятивистскую массу частиц в системе отсчета, связанной с центром инерции. 5.23. В лабораторной системе отсчета находятся две частицы. Одна частица с массой покоя т0 движется со скоростью υ=0,6 с, другая с массой покоя 2т0 покоится. Определить скорость Vc центра масс системы частиц. Взаимосвязь массы и энергии * 5.24.Полная энергия тела возросла на ΔE=1 Дж. На сколько при этом изменится масса тела? 5.25.Определить, на сколько должна увеличиться полная энергия тела, чтобы его релятивистская масса возросла на Δm=1 г? 5.26.Вычислить энергию покоя: 1) электрона; 2) протона; 3) α-частицы. Ответ выразить в джоулях и мегаэлектрон-вольтах. 5.27.Известно, что объем воды в океане равен 1,37·109 км3. Определить, на сколько возрастет масса воды в океане, если температура воды повысится на Δt=1 °С. Плотность р воды в океане принять равной 1,03·103 кг/м3. 5.28.Солнечная постоянная С (плотность потока энергии электромагнитного излучения Солнца на расстоянии, равном среднему расстоянию от Земли до Солнца) равна 1,4 кВт/м2. 1. Определить массу, которую теряет Солнце в течение одного года. 2. На сколько изменится масса воды в океане за один год, если предположить, что поглощается 50 % падающей на поверхность океана энергии излучения? При расчетах принять площадь S поверхности океана равной 3,6·108 км2. Кинетическая энергия релятивистской частицы 5.29.Кинетическая энергия Т электрона равна 10 МэВ. Во сколько раз его релятивистская масса больше массы покоя? Сделать такой же подсчет для протона. 5.30. Во сколько раз релятивистская масса протона больше релятивистской массы электрона, если обе частицы имеют одинаковую кинетическую энергию Т= 1 ГэВ? 5.31. Электрон летит со скоростью υ=0,8 с. Определить кинетическую энергию Т электрона (в мегаэлектрон-вольтах). 5.32. При какой скорости υ кинетическая энергия любой частицы вещества равна ее энергии покоя? 5.33. Определить скорость VEэлектрона, если его кинетическая энергия равна: 1) Т=4 МэВ; 2) T=1 кэВ. 5.34. Найти скорость V протона, если его кинетическая энергия равна: 1) T=1 МэВ; 2) T=1 ГэВ.
5.35. Показать, что релятивистское выражение кинетической 5.36. Какая относительная ошибка будет допущена при вычисле- 5.37. Две релятивистские частицы движутся навстречу друг другу с одинаковыми (в лабораторной системе отсчета) кинетическими энергиями, равными их энергии покоя. Определить: 1) скорости частиц в лабораторной системе отсчета; 2) относительную скорость сближения частиц (в единицах с); 3) кинетическую энергию (в единицах т0с2) одной из частиц в системе отсчета, связанной с другой частицей. Связь энергии релятивистской частицы с ее импульсом 5.38. Показать, что выражение релятивистского импульса через 5.39. Определить импульс р частицы (в единицах m0с), если ее кинетическая энергия равна энергии покоя. 5.40. Определить кинетическую энергию Т релятивистской частицы (в единицах 5.41. Кинетическая энергия релятивистской частицы равна ее энергии покоя. Во сколько раз возрастет импульс частицы, если ее кинетическая энергия увеличится в n=4 раза? 5.42. Импульс р релятивистской частицы равен 5.43. При неупругом столкновении частицы, обладающей импуль- 5) кинетическую энергию частицы до столкновения и кинетическую энергию составной частицы (в единицах т0с2). 5.44. Частица с кинетической энергией
12 |



 * Задачи на эту тему, в условиях которых речь идет о ядерных превращениях, помещены в § 43.
* Задачи на эту тему, в условиях которых речь идет о ядерных превращениях, помещены в § 43.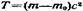 при υ<<c переходит в соответствующее выра-
при υ<<c переходит в соответствующее выра- воспользоваться класси-
воспользоваться класси- ? Вычисления выполнить для двух случаев: 1) υ=
? Вычисления выполнить для двух случаев: 1) υ= при
при  переходит
переходит ), если ее импульс
), если ее импульс 
 . Под действием внешней силы импульс частицы увеличился в два раза. Во сколько раз возрастет при этом энергия частицы: 1) кинетическая? 2) полная?
. Под действием внешней силы импульс частицы увеличился в два раза. Во сколько раз возрастет при этом энергия частицы: 1) кинетическая? 2) полная? , и такой же покоящейся частицы образуется составная
, и такой же покоящейся частицы образуется составная налетает на дру-
налетает на дру-