 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Релятивистское изменение длин 12
РЕЛЯТИВИСТСКАЯ МЕХАНИКА. Основные формулы
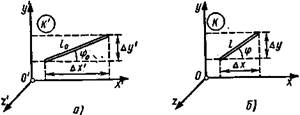
В специальной теории относительности рассматриваются только инерциальные системы отсчета. Во всех задачах считается, что оси у, у' и z, z' сонаправлены, а относительная скорость υ0 системы координат К' относительно системы К направлена вдоль общей оси хх' (рис. 5.1). • Релятивистское (лоренцево) сокращение длины стержня
где l0 — длина стержня в системе координат К' , относительно которой стержень покоится (собственная длина). Стержень параллелен оси х'; l—
длина стержня, измеренная в системе К, относительно которой он движется со скоростью υ; с — скорость распространения электромагнитного излучения.
• Релятивистское замедление хода часов
где Δt0 — интервал времени между двумя событиями, происходящими в одной точке системы K', измеренный по часам этой системы (собственное время движущихся часов); Δt — интервал времени между двумя событиями, измеренный по часам системы K. • Релятивистское сложение скоростей
где υ' — относительная скорость (скорость тела относительно системы K'); υ0 — переносная скорость (скорость системы K' относительно К), υ0 — абсолютная скорость (скорость тела относительно системы К). В теории относительности абсолютной скоростью называется скорость тела в системе координат, условно принятой за неподвижную. • Релятивистская масса
где т0 — масса покоя; β — скорость частицы, выраженная в долях скорости света • Релятивистский импульс
• Полная энергия релятивистской частицы
где Т — кинетическая энергия частицы; • Связь полной энергии с импульсом релятивистской частицы
• Связь кинетической энергии с импульсом релятивистской частицы
Примеры решения задач Пример 1. Космический корабль движется со скоростью υ=0,9 с по направлению к центру Земли. Какое расстояние l пройдет этот корабль в системе отсчета, связанной с Землей (K-система), за интервал времени Δt0=1 с, отсчитанный по часам, находящимся в космическом корабле (K'-система)? Суточным вращением Земли и ее орбитальным движением вокруг Солнца пренебречь. Решение. Расстояние l, которое пройдет космический корабль в системе отсчета, связанной с Землей (K-система), определим по формуле
После вычислений найдем l=619 Мм.
Пример 2.В лабораторной системе отсчета (K-система) движется стержень со скоростью υ=0,8 с . По измерениям, произведенным в K-системе, его длина l оказалась равной 10 м, а угол φ, который он составляет с осью х, оказался равным 30° . Определить собственную длину l0 стержня в K'-системе, связанной со стержнем, и угол φ0, который он составляет с осью х' (рис. 5.2).
Решение. Пусть в K'-системе стержень лежит в плоскости х'О'у'. Из рис. 5.2, а следует, что собственная длина l0 стержня и угол φ0, который он составляет с осью х', выразятся равенствами
В K-системе те же величины окажутся равными (рис. 5.2, б)
Заметим, что при переходе от системы К.' к К размеры стержня в направлении оси у не изменятся, а в направлении оси х претерпят релятивистское (лоренцево) сокращение, т. е.
С учетом последних соотношений собственная длина стержня выразится равенством
или
Заменив в этом выражении
Подставив значения величин l0=15(3 м. Для определения угла
откуда
Подставив значения φ и β в это выражение и произведя вычисления, получим
Пример 3.Кинетическая энергия Т электрона равна 1 МэВ. Определить скорость электрона. Решение. Релятивистская формула кинетической энергии
Выполнив относительно β преобразования, найдем скорость частицы, выраженную в долях скорости света (β=υ/c):
где E0 — энергия покоя электрона (см. табл. 22). Вычисления по этой формуле можно производить в любых единицах энергии, так как наименования единиц в правой части формул сократятся и в результате подсчета будет получено отвлеченное число. Подставив числовые значения Е0и Т в мега электрон-вольтах, получим β=0,941. υ = 2,82-108 м/с. Чтобы определить, является ли частица с кинетической энергией Т релятивистской или классической, достаточно сравнить кинетическую энергию частицы с ее энергией покоя. Если
Пример 4. Определить релятивистский импульс р и кинетическую энергию Т электрона, движущегося со скоростью υ =0,9 с (где с — скорость света в вакууме). Решение. Релятивистский импульс
После вычисления по формуле (1) получим
В релятивистской механике кинетическая энергия Т частицы определяется как разность между полной энергией E и энергией покоя Е0этой частицы, т. е.
Так как
или окончательно
Сделав вычисления, найдем T=106 фДж. Во внесистемных единицах энергия покоя электрона m0с2=0,51 МэВ. Подставив это значение в формулу (2), получим Т=0,66 МэВ. Пример 5.Релятивистская частица с кинетической энергией T=т0c2 (m0 — масса покоя частицы) испытывает неупругое столкновение с такой же покоящейся (в лабораторной системе отсчета) частицей. При этом образуется составная частица. Определить: 1) релятивистскую массу т движущейся частицы; 2) релятивистскую массу т' и массу покоя m0' составной частицы; 3) ее кинетическую энергию Т'. Решение. 1. Релятивистскую массу m движущейся частицы 2. Для того чтобы найти релятивистскую массу составной частицы, воспользуемся тем, что суммарная релятивистская масса частиц сохраняется *: m+m0=m', где т+т0 — суммарная релятивистская масса частиц до столкновения; т' — релятивистская масса составной частицы. Так как т—2т0 , то
Массу покоя m0' составной частицы найдем из соотношения
Так как
Релятивистский импульс
Подставив выражения υ' и т' в формулу (I), найдем массу покоя составной частицы:
3. Кинетическую энергию Т' составной релятивистской частицы найдем как разность полной энергии т'с2и энергии покоя т0'с2 составной частицы:
Подставив выражения т' и m0', получим
· Этот закон см., например, в кн.: Савельев И. В. Куре общей физики. М., 1977. Т. I, §70.
Задачи Релятивистское изменение длин и интервалов времени 5.1. Предположим, что мы можем измерить длину стержня с точностью Δl=0,1 мкм. При какой относительной скорости и двух инерциальных систем отсчета можно было бы обнаружить релятивистское сокращение длины стержня, собственная длина l0 которого равна 1 м? 5.2. Двое часов после синхронизации были помещены в системы координат К и К', движущиеся друг относительно друга. При какой скорости и их относительного движения возможно обнаружить релятивистское замедление хода часов, если собственная длительность τ0 измеряемого промежутка времени составляет 1 с? Измерение времени производится с точностью Δτ=10 пс. 5.3. На космическом корабле-спутнике находятся часы, синхронизированные до полета с земными. Скорость υ0 спутника составляет 7,9 км/с. На сколько отстанут часы на спутнике по измерениям земного наблюдателя по своим часам за время τ0=0,5 года? 5.4. Фотонная ракета движется относительно Земли со скоростью υ=0,6 с. Во сколько раз замедлится ход времени в ракете с точки зрения земного наблюдателя? 5.5. В системе К' покоится стержень, собственная длина l0 которого равна 1 м. Стержень расположен так, что составляет угол φ0=45° с осью x'. Определить длину l стержня и угол φ в системе K, если скорость υ о системы K' относительно К равна 0,8 с. 5.6. В системе К находится квадрат, сторона которого параллельна оси х'. Определить угол φ между его диагоналями в системе К, если система К' движется относительно К со скоростью υ=0,95 с. 5.7. В лабораторной системе отсчета (K-система) пи-мезон с момента рождения до момента распада пролетел расстояние l=75 м. Скорость υ пи-мезона равна 0,995 с. Определить собственное время жизни τ0 мезона. 5.8. Собственное время жизни τ0 мю-мезона равно 2 мкс. От точки рождения до точки распада в лабораторной системе отсчета мю-мезон пролетел расстояние l=6 км. С какой скоростью υ (в долях скорости света) двигался мезон? 12 |






 ,
, , ИЛИ
, ИЛИ  ,
,
 , или
, или 

 — ее энергия покоя. Частица называется релятивистской, если скорость частицы сравнима со скоростью света, и классической, если υ<<с.
— ее энергия покоя. Частица называется релятивистской, если скорость частицы сравнима со скоростью света, и классической, если υ<<с.

 (1)
(1) —интервал времени, отсчитанный в K-системе отсчета.
—интервал времени, отсчитанный в K-системе отсчета. Подставив
Подставив в формулу (1), получим
в формулу (1), получим
 (1)
(1) (2)
(2) (3)
(3)

 на
на  (рис. 5.2, б), получим
(рис. 5.2, б), получим
 в это выражение и произведя
в это выражение и произведя воспользуемся соотношениями (1), (2) и (3):
воспользуемся соотношениями (1), (2) и (3): , или
, или 


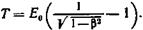
 (1)
(1) , то
, то , частицу можно считать классической. В этом
, частицу можно считать классической. В этом , или
, или 
 (1)
(1)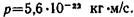

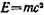 и
и  , то, учитывая зависимость массы от
, то, учитывая зависимость массы от
 (2)
(2) . Так как
. Так как  , то m=
, то m=
 (1)
(1)
 , то
, то
 . Учитывая, что
. Учитывая, что  ,
, ,
,
 , или
, или 

