 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Свойства плотности распределения. 12
1) Плотность распределения – неотрицательная функция.
2) Несобственный интеграл от плотности распределения в пределах от - ¥ до ¥ равен единице.
Пример 1. Случайная величина подчинена закону распределения с плотностью:
Требуется найти коэффициент а, построить график плотности вероятностей и определить вероятность того, что случайная величина попадет в интервал от 0 до Решение: Для нахождения коэффициента а воспользуемся свойством
Находим вероятность попадания случайной величины в заданный интервал.
Числовые характеристики случайных величин. Закон распределения полностью характеризует случайную величину. Однако, когда невозможно найти закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины. Эти величины определяют некоторое среднее значение (центр), вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения. Математическое ожидание. Наиболее распространенной характеристикой центра распределения значений случайной величины является математическое ожидание. Определение. Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.
Определение. Математическим ожиданиемнепрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл на этом отрезке от произведения переменной х на плотность вероятностей f(x):
Если возможные значения непрерывной случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:
С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания. 1) Математическое ожидание постоянной величины равно самой постоянной.
2) Постоянный множитель можно выносить за знак математического ожидания.
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Это свойство справедливо для произвольного числа случайных величин.
4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.
Это свойство также справедливо для произвольного числа случайных величин.
Дисперсия.
Математическое ожидание не может полностью характеризовать случайную величину. Кроме математического ожидания надо ввести величину, которая характеризует отклонение значений случайной величины от математического ожидания. Это отклонение равно разности между случайной величиной и ее математическим ожиданием. При этом математическое ожидание отклонения равно нулю. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль.
Определение. Дисперсией (рассеиванием) случайной величины (и дискретной и непрерывной) называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Дисперсия дискретной сл. величины задается формулой:
Дисперсия непрерывной сл. величины определяется так:
Замечание: При этом предполагается, что несобственный интеграл сходится.
Однако, на практике подобный способ вычисления дисперсии не всегда удобен, т.к. приводит при большом количестве значений случайной величины к громоздким вычислениям. Поэтому применяется другой способ.
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания.
Т.о., для дискретной сл. величины формула для вычисления дисперсии такова:
для практического вычисления дисперсии непрерывной сл. величины используется формула:
Свойства дисперсии.
1) Дисперсия постоянной величины равна нулю.
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
Справедливость этого равенства вытекает из свойства 2.
12 |






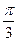 .
. .
.



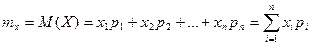











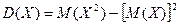
 ,
,



