 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Глава 2. Случайные величины. 12
§1. Дискретные и непрерывные случайные величины
Рассматривая случайные события, сталкивались с такими, которые состоят в появлении того или иного числа. Например, при бросании игрального кубика выпавшие очки выражаются числом от 1 до 6. Наперед определить какое именно число появится в результате опыта невозможно. В этом смысле число выпавших очков при бросании кубика есть величина случайная (СВ). Случайная величина является количественной характеристикой случайного результата опыта. Определение. Случайной величинойназывается величина, которая в результате опыта может принимать то или иное числовое значение, причем заранее неизвестно какое именно. Обозначают · случайные величины заглавными буквами латинского алфавита: X, Y, Z, U, V … · значения случайных величин малыми буквами с индексами: x1, x2,…y1, y2,… Примеры случайных величин: 1) X – число попаданий в мишень при двух выстрелах; возможные значения этой СВ: x1 = 0 (нет ни одного попадания), x2 = 1 (одно попадание), x3 = 2 (два попадания). 2) Y – рост случайно выбранного человека; Возможные значения СВ Y перечислить нельзя, можно лишь указать промежуток, которому эти значения принадлежат: ymin – ymax. Примеры 1) и 2) показывают, что случайные величины можно разделить на две категории: те, которые принимают отдельные, изолированные значения на числовой прямой и те, которые заполняют некоторый промежуток на числовой прямой. Эти категории образуют Дискретные и Непрерывные случайные величины.
Определение. Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения образующие счетное множество (множество, элементы которого могут быть занумерованы).
Это множество может быть как конечным, так и бесконечным. Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать счетное, хотя и бесконечное количество значений.
Определение. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка. Очевидно, что число возможных значений непрерывной случайной величины бесконечно.
Для задания случайной величины недостаточно просто указать ее значение, необходимо также указать вероятность этого значения.
§2. Закон распределения дискретной случайной величины.
Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретнойслучайной величины. Закон распределения может быть задан аналитически, в виде таблицы или графически. Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения. Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
Пример. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятности числа попаданий и построить многоугольник распределения. Решение: Найдем вероятности пяти попаданий из пяти возможных, четырех из пяти, трех из пяти, двух из пяти, одного из пяти и нуля из пяти по формуле Бернулли:
Проверим, что сумма вероятностей равна единице: 0,01024+0,0768+0,2304+0,3456+0,2592+0,07776=1. Запишем ряд (таблицу) распределения СВ:
Представим графически зависимость числа попаданий от их вероятностей. При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности. §3. Функция распределения случайной величины.
Задание случайной величины путем определения значений этой величины и вероятностей этих значений применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально. Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин. Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. P(Х < x), обозначим через F(x). Определение. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее аргумента х.
Функцию распределения также называют интегральной функцией. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения. Для дискретной случайной величины функция распределения имеет вид:
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х. Так, построим функцию распределения для примера, рассмотренного в §2:
Если 0 < x ≤ 1, то меньше такого х только одно значение: x1 = 0 и его вероятность P(X<x) = 0,07776. Если 1 < x ≤ 2, то меньше такого х только два значения: x1 = 0 и x2 = 1, вероятность того, что X<x будет равна для таких х сумме вероятностей значений x1 = 0 и x2 = 1: P(X<x) = 0,07776 + 0,2592 = 0,33696. Если 2 < x ≤ 3, то меньше такого х три значения: x1 = 0, x2 = 1 и х3 =2, вероятность того, что X<x будет равна для таких х сумме вероятностей значений x1 = 0, x2 = 1, х3 =2: P(X<x) = 0,07776 + 0,2592 + 0,3456 = 0,68256. Если 3 < x ≤ 4, то меньше такого х четыре значения: x1 = 0, x2 = 1, х3 =2 и х4 = 3, вероятность того, что X<x будет равна для таких х сумме вероятностей значений x1 = 0, x2 = 1, х3 =2, х4 = 3: P(X<x) = 0,07776 + 0,2592 + 0,3456 + 0,2304 = 0,91296. Если 4 < x ≤ 5, то меньше такого х пять значений: x1 = 0, x2 = 1, х3 =2, х4 = 3,х5 = 4, вероятность того, что X<x будет равна для таких х сумме вероятностей значений x1 = 0, x2 = 1, х3 =2, х4 = 3, х5 = 4: P(X<x) = 0,07776 + 0,2592 + 0,3456 + 0,2304 + 0,0768 = 0,98976. Если x > 5, то меньше такого х все шесть значений: вероятность того, что X<x будет равна для таких х сумме всех вероятностей: P(X<x) = 0,07776 + 0,2592 + 0,3456 + 0,2304 + 0,0768 + 0,01024 =1.
Таким образом, запишем функцию распределения:
Построим ее график:
Функция распределения дискретной случайной величины Х разрывная и возрастает скачками при переходе через каждое значение хi. Для непрерывной СВ функция распределения является непрерывной. 12 |



 ,
, 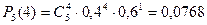 ,
,  ,
, 






 Если х ≤ 0, то значений случайной величины, меньше такого х нет, т.е. P(X<x) = 0;
Если х ≤ 0, то значений случайной величины, меньше такого х нет, т.е. P(X<x) = 0;
