 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Пример расчета однофазной цепи 12
По заданным значениям активных и реактивных сопротивлений и напряжению источника определить токи во всех ветвях схемы и падения напряжения на ее участках. Определить комплекс полной мощности, активную и реактивную мощность. Расчет произвести комплексным методом. Выполнить проверку правильности расчета с использованием баланса активных мощностей схемы. Построить векторную диаграмму. Построить мгновенные значения синусоидальных токов ветвей. Исходные данные для расчета приведены в таблице.
Решение: Электрическая цепь на рис. 2.4 состоит из трех ветвей, определим комплексные сопротивления ветвей. Сопротивление первой ветви, состоящей из сопротивления R1 и идеальной катушки индуктивности с комплексным сопротивлением
Сопротивление второй ветви, состоящей из сопротивления R2 и идеальной емкости с комплексным сопротивлением
Сопротивление третьей ветви, состоящей из сопротивления R3 и идеальной катушки индуктивности с комплексным сопротивлением
Вторая и третья ветвь соединены параллельно, поэтому их эквивалентное сопротивление
Эквивалентное сопротивление всей схемы:
Зная эквивалентное сопротивление, можно определить ток в первой ветви:
Затем можно определить напряжения на участках цепи:
Зная напряжение на участке bc можно рассчитать токи
Проверку правильности расчета токов можно выполнить по первому закону Кирхгофа в комплексной форме:
Так как первый закон Кирхгофа выполняется, значит, расчет токов выполнен верно. Комплекс полной мощности:
где
При этом действительная часть комплекса полной мощности равна активной мощности потребляемой схемой
а мнимая часть комплекса полной мощности равна реактивной мощности схемы
Рис. 2.5. Векторная диаграмма токов и напряжений
Выражения для мгновенных значений токов можно получить из комплексных значений записанных в показательной форме:
Действующее значение тока I1 = 0.724 А, а фазовый сдвиг
Аналогично для остальных токов:
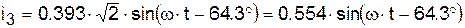 А. А. Графики мгновенных значений токов приведены на рис. 2.6. Рис. 2.6. Мгновенные значения токов
Расчет трехфазных цепей Расчет трехфазных трехпроводных электрических цепей в несимметричном режиме производится комплексным методом, так как в этом режиме токи и напряжения фаз не равны между собой и основные соотношения между линейными и фазными величинами не выполняются. Пример расчета трехфазной цепи при соединении нагрузки звездой: Заданна схема трехфазной трехпроводной цепи (рис. 2.7), с соединением нагрузки звездой и сопротивления фаз нагрузки:
Рис. 2.7. Схема трехфазной цепи с нагрузкой, соединенной звездой
Нагрузка несимметричная, ЭДС трехфазного идеального источника равны: По заданным значениям активных и реактивных сопротивлений фаз нагрузки определить: фазные токи и напряжения на нагрузке, напряжение смещения нейтрали, активную, реактивную, полную мощность. Решение: В несимметричном режиме работы трехпроводной трехфазной цепи, с нагрузкой, соединенной звездой, возникает напряжение смещения нейтрали
Напряжение смещения нейтрали определяется по формуле:
Фазные напряжения на нагрузке в несимметричном режиме определяются по второму закону Кирхгофа:
Фазные токи нагрузки равны линейным токам и определяются по формулам:
Сумма фазных токов, по первому закону Кирхгофа, должна быть равна нулю:
Комплекс полной мощности трехфазной нагрузки, соединенной звездой:
Активная мощность Р = 476.426 Вт, а реактивная мощность Q = 59.553 ВА. Пример расчета трехфазной цепи при соединении нагрузки треугольником: Заданна схема трехфазной трехпроводной цепи (рис. 2.8), с соединением нагрузки треугольником и сопротивления фаз нагрузки:
Нагрузка несимметричная, ЭДС трехфазного идеального источника равны: По заданным значениям активных и реактивных сопротивлений фаз нагрузки определить: фазные токи и напряжения на нагрузке, фазные напряжения на нагрузке, активную, реактивную, полную мощность.
Рис. 2.8. Схема трехфазной цепи при соединении нагрузки треугольником Решение: В несимметричном режиме работы трехпроводной трехфазной цепи, с нагрузкой, соединенной треугольником, фазные напряжения на нагрузке равны линейным напряжениям источника питания. Величины этих напряжений можно определить по второму закону Кирхгофа:
При известных комплексных сопротивлениях фаз нагрузки:
Фазные токи рассчитываются по закону Ома:
Линейные токи определяются по первому закону Кирхгофа:
Сумма линейных токов, по первому закону Кирхгофа, должна быть равна нулю: Комплекс полной мощности трехфазной нагрузки, соединенной треугольником:
где: Активная мощность Р = 338.709 Вт, а реактивная мощность Q = 435.483 ВА. 12 |



 :
: Ом.
Ом. :
: Ом.
Ом.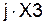 :
: Ом.
Ом.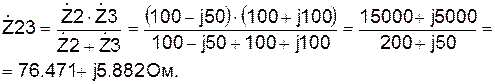
 Ом.
Ом. А.
А. В,
В,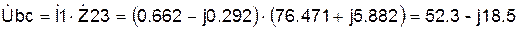 В.
В. А,
А,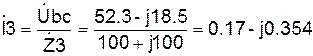 А.
А. , или
, или .
. ,
, - сопряженный комплекс тока
- сопряженный комплекс тока  . Если
. Если  А, то сопряженный комплекс
А, то сопряженный комплекс  А. Таким образом, комплекс полной мощности равен
А. Таким образом, комплекс полной мощности равен ВА.
ВА. Вт,
Вт, ВА.
ВА.
 А.
А. , таким образом мгновенное значение тока равно
, таким образом мгновенное значение тока равно А.
А. А.
А. А.
А. А.
А.
 , Ом
, Ом , Ом
, Ом , Ом
, Ом , Ом
, Ом , Ом
, Ом , Ом
, Ом
 В,
В,  ,
,  В.
В. . Величину этого напряжения можно определить по методу двух узлов. При известных комплексных сопротивлениях и проводимостях фаз нагрузки:
. Величину этого напряжения можно определить по методу двух узлов. При известных комплексных сопротивлениях и проводимостях фаз нагрузки: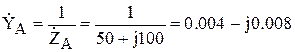 См,
См, Ом;
Ом; См;
См; Ом;
Ом; См;
См; Ом.
Ом.
 В;
В;

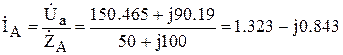 А;
А; А;
А; А.
А. .
. где:
где:  - сопряженные комплексы фазных токов.
- сопряженные комплексы фазных токов. , Ом
, Ом , Ом
, Ом , Ом
, Ом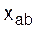 , Ом
, Ом , Ом
, Ом , Ом
, Ом
 В;
В; В;
В; В.
В. Ом;
Ом; Ом;
Ом; Ом.
Ом. А;
А; А;
А; А.
А. А;
А; А;
А; А.
А.
 - сопряженные комплексы фазных токов.
- сопряженные комплексы фазных токов.