 ПОЗНАВАТЕЛЬНОЕ
| Расчет цепей постоянного тока 12
Задание для контрольной работы Контрольная работа охватывает три основных раздела электротехники: · линейные и нелинейные электрические цепи постоянного тока (1, 2, задачи); · цепи однофазного переменного тока (3 задача); · трехфазные цепи (4 задача). Задача №1 По данным своего варианта (табл. 1) выбрать расчетную схему (рис. 1.1) и исходные данные для расчета (табл. 2). Определить количество узлов и ветвей в схеме, обозначить узлы (a, b, c …) и условно положительные направления токов в ветвях схемы и напряжений на ее участках. Определить: · токи во всех ветвях схемы, расчет произвести методом контурных токов, выполнить проверку правильности расчета методом баланса мощностей; · ток в ветви с сопротивлением R6 методом эквивалентного генератора. Для определения эдс эквивалентного генератора в режиме холостого хода использовать метод двух узлов, а для расчета внутреннего сопротивления эквивалентного генератора (тока короткого замыкания) – метод наложения.
Задача №2 По данным своего варианта (табл. 1) выбрать схему (рис. 1.2) и исходные данные для расчета (табл. 3). Для заданной нелинейной цепи рассчитать токи в ветвях графическим методом. Выполнить проверку правильности расчета с использованием законов Кирхгофа.
Таблица 1
Таблица 2
Таблица 3
Рис. 1.1. Варианты схем для расчета к задаче № 1
Рис. 1.2. Варианты схем к задаче №2
Рис. 1.3. Вольт-амперные характеристики нелинейных элементов Задача №3
По данным своего варианта (табл. 4) выбрать расчетную схему (рис. 1.4) и исходные данные для расчета (табл. 5). По заданным значениям активных и реактивных сопротивлений и напряжению источника определить токи во всех ветвях схемы и падения напряжения на ее участках. Определить комплекс полной мощности, активную и реактивную мощность. Расчет произвести комплексным методом. Выполнить проверку правильности расчета с использованием баланса активных мощностей схемы. Построить векторную диаграмму. Построить мгновенные значения синусоидальных токов ветвей.
Рис. 1.4. Варианты схем к задаче 3 Таблица 4
Таблица 5
Таблица 6
Задача №4 По данным своего варианта (табл. 4) выбрать схему (рис. 1.5) и исходные данные для расчета (табл. 6), трехфазной трехпроводной цепи в которой к идеальному трехфазному источнику присоединены две нагрузки. Одна из них соединена звездой, другая – треугольником. Обе нагрузки нессимметричные. ЭДС трехфазного идеального источника равны:
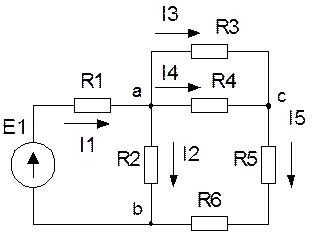
Рис. 1.5. Варианты схем к задаче №4 По заданным значениям активных и реактивных сопротивлений фаз нагрузки определить: · для нагрузки, соединенной звездой - фазные токи и напряжения на нагрузке и напряжение смещения нейтрали, активную, реактивную, полную мощность. · для треугольника – фазные и линейные токи, фазные напряжения, активную, реактивную, полную мощность. Расчет произвести комплексным методом. Построить векторные диаграмму токов и напряжений для звезды и треугольника. Примеры решения задач Расчет цепей постоянного тока Пример 1 Рассчитать токи в ветвях схемы показанной на рис. 2.1. Если Е1=100В, R1=100 Ом, R2=100 Ом, R3=60 Ом, R4=40 Ом, R5=56 Ом, R6=20 Ом.
Так как электрическая цепь содержит один источник электрической энергии, то расчет целесообразно вести методом эквивалентных преобразований. Перед началом расчета необходимо расставить направление токов, определить количество узлов и ветвей. Направление токов на схеме соответствует направлению ЭДС источника (см. рис. 2.1), схема содержит пять ветвей и три узла (a, b, c). В схеме на рис. 2.1 сопротивления R3 и R4 соединены параллельно, их эквивалентное сопротивление равно:
Сопротивления R34, R5 и R6 соединены последовательно, их эквивалентное сопротивление равно:
Сопротивление R2 и сопротивление R3456 соединены параллельно, следовательно:
Сопротивление R1 соединено последовательно с R23456 следовательно, эквивалентное сопротивление всей схемы равно:
Ток, потребляемый от источника ЭДС:
Чтобы рассчитать остальные токи схемы необходимо определить напряжение между узлами a и b:
Зная напряжение
Чтобы рассчитать токи, протекающие по сопротивлениям R3 и R4 необходимо определить напряжение на участке ac:
Зная это напряжение, определим токи:
Выполняем проверку правильности решения с помощью первого закона Кирхгофа для узлов a и с: I1 - I2 - I3 - I4 = 1А – 0.5А – 0.2А – 0.3А = 0, I3 + I4 – I5 = 0.2А + 0.3А – 0.5А = 0. Так как законы Кирхгофа выполняются, то расчет выполнен правильно. Пример 2 Рассчитать токи в ветвях схемы показанной на рис. 2.2. Если Е1=100В, Е2=75В, Е3=50В R1=100 Ом, R2=50 Ом, R3=20 Ом, R4=40 Ом, R5=40 Ом.
В соответствии с методом двух узлов межузловое напряжение будет равно:
Зная межузловое напряжение, определяем токи в ветвях, используя второй закон Кирхгофа:
Выполняем проверку правильности решения с помощью первого закона Кирхгофа для узла a: I1 + I2 - I3 - I4 = 0.826А + 1.151А – 0.291А – 1.686А = 0, Так как законы Кирхгофа выполняются, то расчет выполнен правильно. Пример 3 Решить задачу, приведенную в примере 2 с помощью метода наложения.
Так как схема на рис. 2.2 содержит три источника ЭДС, то расчет одной сложной цепи сводится к расчету трех простых цепей, показанных на рис. 2.3. Направления токов в исходной схеме показаны на Рис. 1.5, в схемах на рис. 2.3 направления токов обозначены в соответствии с направлением источников ЭДС. Рассчитаем первую схему (рис. 2.3, а). Сопротивления R2, R34 и R5 соединены параллельно, их эквивалентное сопротивление равно: Сопротивления R1 и R23456 соединены последовательно, следовательно эквивалентное сопротивление первой схемы:
Ток, потребляемый от источника Е1, равен:
Чтобы определить токи в оставшихся ветвях необходимо найти напряжение: Токи в ветвях:
Рассчитаем вторую схему (рис. 2.3, б). Сопротивления R1, R34 и R5 соединены параллельно, их эквивалентное сопротивление равно:
Сопротивления R2 и R13456 соединены последовательно, следовательно эквивалентное сопротивление первой схемы:
Ток, потребляемый от источника Е2, равен:
Чтобы определить токи в оставшихся ветвях необходимо найти напряжение: Токи в ветвях:
Рассчитаем третью схему (рис. 2.3, в). Сопротивления R1, R34 и R2 соединены параллельно, их эквивалентное сопротивление равно:
Сопротивления R5 и R1234 соединены последовательно, следовательно эквивалентное сопротивление первой схемы:
Ток, потребляемый от источника Е3, равен:
Чтобы определить токи в оставшихся ветвях необходимо найти напряжение: Токи в ветвях:
В качестве положительных направлений токов принимаем их направления на исходной схеме (рис. 2.2). С учетом этого токи схемы на рис. 2.2 определятся как:
12 |










 , Ом
, Ом , Ом
, Ом , Ом
, Ом , Ом
, Ом , Ом
, Ом , Ом
, Ом , Ом
, Ом , Ом
, Ом , Ом
, Ом , Ом
, Ом , Ом
, Ом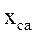 , Ом
, Ом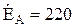 В,
В,  ,
,  В.
В.
 Решение:
Решение: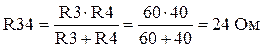 .
. .
. .
. .
.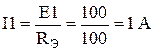 .
. .
. можно определить токи:
можно определить токи: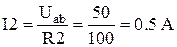 ,
, .
. .
. ,
, .
. Решение:
Решение: Перед началом расчета необходимо расставить направление токов, определить количество узлов и ветвей. Так как в схеме несколько источников ЭДС используем условно-положительные направления токов. На схеме направление токов соответствует направлению ЭДС в активных ветвях, а в пассивной ветви выбрано произвольно (см. рис. 2.2), схема содержит четыре ветви и два узла (a, b). Так как в схеме два узла и несколько источников ЭДС, то расчет целесообразно вести методом двух узлов. Обозначим направление межузлового напряжения
Перед началом расчета необходимо расставить направление токов, определить количество узлов и ветвей. Так как в схеме несколько источников ЭДС используем условно-положительные направления токов. На схеме направление токов соответствует направлению ЭДС в активных ветвях, а в пассивной ветви выбрано произвольно (см. рис. 2.2), схема содержит четыре ветви и два узла (a, b). Так как в схеме два узла и несколько источников ЭДС, то расчет целесообразно вести методом двух узлов. Обозначим направление межузлового напряжения  ,
, ,
, ,
, .
. .
. ,
, ,
, ,
, .
.
 Решение:
Решение: .
. .
. .
. .
. ,
,
 .
.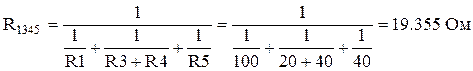 .
. .
. .
.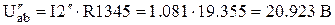 .
. ,
, ,
, .
. .
. .
. .
. .
. ,
, ,
, .
. ,
, ,
, ,
,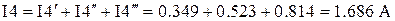 .
.