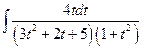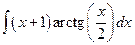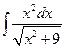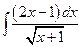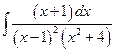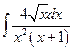ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Площадь криволинейного сектора. 12
Некоторые плоские фигуры удобно описывать в полярных координатах
Криволинейный сектор в полярных координатах задаётся в виде
где функция
x
Площадь криволинейного сектора равна
2) Длина дуги кривой.Пусть кривая
Если кривая
Длина дуги в полярных координатах. Частный случай параметрического задания кривой – её задание в полярных координатах:
3) Объем тела вращения. Многие пространственные объекты удобно представлять себе как множество точек, заметаемых той или иной плоской фигурой при её вращении в трёхмeрном пространстве вокруг какой−нибудь прямой, например, вокруг оси
y = f(x)
a b x
z
Пусть тело получено вращением вокруг оси
4) Площадь поверхности тела вращения. В той же ситуации, что и в пункте 3), площадь боковой поверхности тела вращения равна
Контрольная работа №1 Вариант 0
Решение варианта 0 1)
2)
3)
4)
5)
6)
7) Найдем интеграл
Ответ:
8) Разложим интегрируемую функцию на простые дроби
Приравняв числители, получим
Для нахождения коэффициентов A, B, C подставим в данное тождество три различных значения переменной x:
Таким образом
Контрольная работа №2 Вариант 0
Решение варианта 0 1)
2)
3)
4) Поделим с остатком числитель подынтегральной функции на знаменатель.
5) Разложим интегрируемую функцию на простые дроби
Приравняв числители, получим
откуда
Таким образом
6)
Откуда
Таким образом
7)
8)
Таким образом
9)
10)
11)
Таким образом,
Ответ:
12)
Вычисляем первый из двух оставшихся интегралов:
Второй интеграл равен
Ответ:
13)
14)
15)
16)
17)
18)
19)
Разложим интегрируемую функцию на простые дроби. Поскольку дробь неправильная, сначала поделим с остатком ее числитель на знаменатель
Приравняв числители, получим
Откуда
Таким образом
20)
Приравняв числители, получим
Откуда
Таким образом
i) ii)
Ответ:
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
Вариант 12
Вариант №13
Вариант 14
Вариант №15
Вариант №16
Вариант №17
Вариант №18
Вариант 19
Вариант 20 12
©2015 www.megapredmet.ru Все права принадлежат авторам размещенных материалов. |



 , где
, где  – полярный радиус точки
– полярный радиус точки  , а
, а 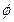 – её полярный угол (угол, на который надо повернуть в направлении против часовой стрелки положительный луч оси
– её полярный угол (угол, на который надо повернуть в направлении против часовой стрелки положительный луч оси  до совмещением с радиус–вектором точки
до совмещением с радиус–вектором точки  . Формулы полярной замены:
. Формулы полярной замены:
 ,
, определяет границу сектора.
определяет границу сектора. y
y


 задана как график функции
задана как график функции 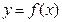 , определенной на отрезке
, определенной на отрезке  . Тогда длина L дуги
. Тогда длина L дуги 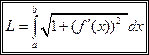

 , тогда
, тогда
 . Тогда
. Тогда  ,
,  и прямое дифференцирование и подстановка производных в формулу длины дуги, заданной в параметрическом виде, дает
и прямое дифференцирование и подстановка производных в формулу длины дуги, заданной в параметрическом виде, дает
 y
y , осью
, осью  ,
,  . Тогда его обьём равен
. Тогда его обьём равен









 .
. .
. .
. .
.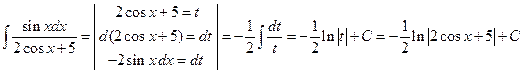 .
.
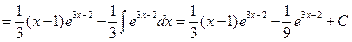 .
.
 .
.
 .
. .
. .
. .
. .
.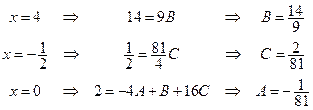



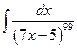



 0
0
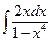
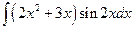

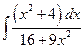




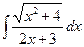





 .
. .
. .
.

 .
.
 .
. ,
,






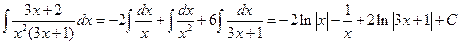



 .
.




 .
.




 .
.



 .
.

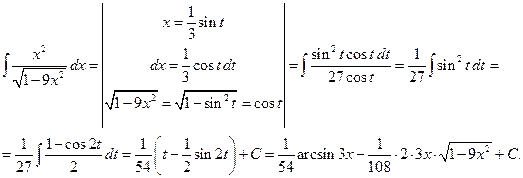

 .
.











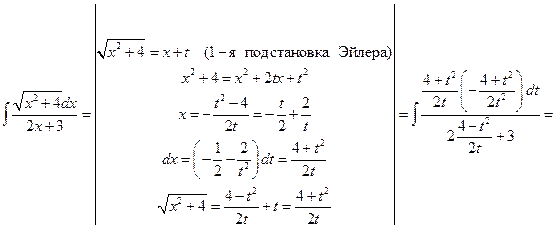
 .
.