 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Интегрирование рациональных функций 12
Кафедра математики и естественнонаучных дисциплин
Борисова О.Н. Интегральное исчисление функций одной переменной
Сборник контрольных задач и методических указаний
Королев, 2009 Борисова О.Н. Интегральное исчисление функций одной переменной. Сборник контрольных задач и методических указаний. - Королев: КИУЭС, 2009, 54 с.
Рецензенты: к.п.н., доцент Федосеева З.Р.
Сборник включает в себя задачи контрольных работ по курсу «Математика», раздел интегральное исчисление, и методических указаний по их решению. Предназначен для проведения практических занятий, контрольных работ, а также для самостоятельной работы студентов всех специальностей, изучающих данный курс.
Введение
Данное пособие содержит подборки задач, предназначенных как для самостоятельного решения, так и для проведения контрольных работ по курсу «Интегральное исчисление функций одного вещественного переменного». Все разделы содержат краткие формулировки основных понятий и теорем, необходимых для решения задач. В сборник включено 3 контрольные работы, каждая из которых приводится в 25 различных вариантах. Каждой контрольной работе предшествует разбор типового варианта. Неопределённый интеграл
Первообразной от непрерывной функции f(x) называется любая функция F(x), для которой выполнено соотношение
Для любой функции f(x) имеется много первообразных, однако все они отличаются друг от друга на константу: если F1(x) и F2(x) – первообразные от f(x), то Совокупность всех первообразных называется неопределенным интегралом от f(x) и обозначается так:
Здесь F(x) − любая фиксированная первообразная. Прямым дифференцированием можно проверить справедливость следующих соотношений.
Частные случаи формулы
Имеется два основных приема вычисления неопределенных интегралов.
Замена переменной Это наиболее часто используемый прием.
Интегрирование по частям Интегрирование по частям позволяет «перебросить» производную с одного множителя, входящему в интегрируемую функцию, на другой
Во многих случаях угадать формулу замены переменной, упрощающей интегрируемую функцию, помогает занесение множителя под знак дифференциала
где
Так как производная постоянной функции равна нулю, а постоянный множитель можно выносить за знак дифференциала, для произвольных постоянных
Рекомендуется запомнить следующие формулы
Разберем типичные ситуации , в которых используется интегрирование по частям.
1) Под знаком интеграла стоит
2) Интеграл вида
3) Интеграл вида
Обозначим F(x) произвольную первообразную функции
Выразим
Интегрирование рациональных функций Рациональной функцией, или рациональной дробью, называется выражение вида Пусть Правильная рациональная дробь называется простой, если она принадлежит к одному из нижеперечисленных типов
Примеры простых дробей:
Любая правильная рациональная дробь может быть представлена как сумма простых дробей с подходящими коэффициентами. Такое разложение находят методом неопределенных коэффициентов, который мы проиллюстрируем на одном конкретном примере. Рассмотрим функцию:
Составим комбинацию простых дробей, в знаменателях которых присутствуют все возможные делители знаменателя исходной функции:
После приведения этих пяти дробей к общему знаменателю получим:
Приравняв числители (1) и (2), получим уравнение
Соотношение (3) должно быть выполнено при всех значениях х. Подставим в (3) пять (по числу неизвестных коэффициентов A, B, C, D, E) различных значений х и получим систему уравнений на A, B, C, D, E:
Можно показать, что у такой системы всегда существует единственное решение. Решив эту систему (например, методом Гаусса), получим требуемое представление
Интегрирование любой простой дроби всегда сводится к интегрированию табличных функций. Приведем несколько наиболее типичных примеров:
1)
2)
3)
1 способ. Интегрирование по частям.
2 способ. Замена переменной. = 12 |



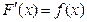 .
. .
. .
.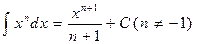






















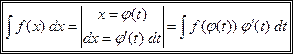 .
.
 ,
, − произвольная первообразная функции
− произвольная первообразная функции  .
.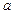 и
и  имеет место формула
имеет место формула .
.





 ,
,  ,
,  , умноженные на многочлен.
, умноженные на многочлен.

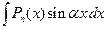 ,
,  ,
,  .
.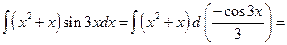





 ,
,  .
.
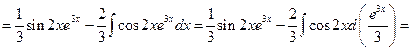



 , получим
, получим
 .
. , где
, где  и
и  − многочлены степени n и m соответственно. Если n
− многочлены степени n и m соответственно. Если n 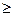 m, дробь
m, дробь  m, то правильной. Неправильную рациональную дробь можно записать в виде суммы многочлена и правильной дроби. Для этого используется следующая процедура деления с остатком многочлена на многочлен (алгоритм Евклида).
m, то правильной. Неправильную рациональную дробь можно записать в виде суммы многочлена и правильной дроби. Для этого используется следующая процедура деления с остатком многочлена на многочлен (алгоритм Евклида). ,
,  при этом
при этом 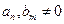 , n
, n  и вычтем получившееся выражение из
и вычтем получившееся выражение из  . В результате получим некоторый многочлен
. В результате получим некоторый многочлен  , степень которого строго меньше
, степень которого строго меньше  , и при этом
, и при этом  . Если степень
. Если степень  все еще больше
все еще больше  , применим описанный прием уже к многочлену
, применим описанный прием уже к многочлену 

 . (1)
. (1)
 (2)
(2) (3)
(3)
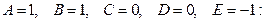

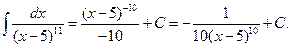

 .
. Кратный неразложимый квадратный многочлен в знаменателе дроби.
Кратный неразложимый квадратный многочлен в знаменателе дроби.



