 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Визначення реакцій у кінематичних парах та зрівноважувальної сили методом кінетостатики 12
3.1.1. Для визначення реакцій у кінематичних парах механізму необхідно розподілити його на структурні групи і розглянути всі сили та моменти, що діють на ланки. Згідно правил структурного аналізу даний механізм розподіляється на первинний механізм (тобто ведучу ланку) та одну структурну групу (групу Ассура), яка складається з ланок 2 та 3 (рис. 3.1).
а б а – первинний механізм; б – структурна група Рисунок 3.1 – Структурний розподіл кривошипно-шатунного механізму
3.1.2. Розглянемо спочатку структурну групу (рис. 3.1, б). Покажемо всі сили та моменти, що діють на ланки 2 та 3, а також реакції, що виникають у кінематичних парах. На ланки структурної групи діють: динамічний момент Мд2, сили ваги другої та третьої ланок
Рисунок 3.2 – Сили та реакції у кінематичних парах, що діють на структурну групу
При побудові необхідно дотримуватися наступних правил. Динамічний момент завжди направлений проти кутового прискорення Реакція дії першої ланки на другу 3.1.3. Розрахуємо величини динамічного моменту, сил ваги та сил інерції.
де
де m2, m3 – маси другої та третьої ланок відповідно, кг (з умови завдання); lAB – довжина ланки АВ, м (з умови завдання); g – прискорення вільного падіння, g=9,8 м/с2; G2 і G3 – сили ваги другої та третьої ланок відповідно, Н.
де
3.1.4. Для знаходження сили опору Мінімальне значення тиску рmin і максимальне його значення рmax та кут нахилу бічних сторін діаграми навантаження задаються викладачем. Масштаб побудови μр діаграми визначається самостійно. Наприклад, для довільно вибраного h (див рис 3.3):
Рисунок 3.3 – Діаграма навантаження (залежність тиску на поршень р від переміщення повзуна SB)
Щоб визначити силу опору для певного положення механізму (надалі – n-го положення), необхідно провести вертикальну пряму з точки Вn до перетину з паралелограмом. Причому слід враховувати, що робочому ходу відповідають більші значення тиску на діаграмі, а холостому – менші його значення. Так, на рисунку 3.3 ділянка аbc відповідає робочому ходу (р.х.), а ділянка adc – холостому ходу (х.х.). 3.1.5. Обчислимо силу опору:
або
де р/ – значення тиску у n-му положенні повзуна при певному h/ (див. рис. 3.3):
Sп – площа поршня:
де Dn – діаметр поршня, мм (з умови завдання). 3.1.6. Реакції 1) Сума моментів усіх сил відносно точки В дорівнює нулю:
де З даного рівняння визначаємо тангенціальну складову реакції дії першої ланки на другу:
Якщо результат одержали зі знаком «–», то напрямок дії реакції змінюється на протилежний. 2) Векторна сума всіх сил, що діють на ланки, дорівнює нулю:
За даним рівнянням рівноваги будуємо векторний силовий багатокутник. Невідомі реакції у рівнянні рівноваги слід записати на початку та в кінці виразу, а всі інші силові фактори - у довільному порядку. 3.1.7. Масштаб побудови багатокутника μр (Н/мм) визначається з огляду на найменшу за модулем силу з усіх, що входять до рівняння (3.16). 3.1.8. Побудуємо векторний силовий багатокутник. Для цього проводимо лінію, паралельну осі ланки АВ, вздовж якої діє реакція
Рисунок 3.4 – Векторний силовий багатокутник
3.1.9. Визначимо числові значення знайдених реакцій:
де μр - масштаб побудови багатокутника, Н/мм. 3.1.10. Сумарний вектор реакції дії першої ланки на другу:
3.1.11. Розглянемо первинний механізм. На нього діють: сила ваги першої ланки
Рисунок 3.5 – Схема сил, що діють на первинний механізм
Реакція опори на первинний механізм 3.1.12. Сила ваги першої ланки:
3.1.13. Реакцію 1) Сума моментів усіх сил відносно точки О1 дорівнює нулю:
де Звідси знаходимо зрівноважувальну силу:
Якщо одержали результат зі знаком «–», напрямок сили змінюємо на протилежний. 2) Векторна сума усіх сил, що діють на першу ланку, дорівнює нулю:
Для знаходження невідомої реакції Примітка. Масштаби побудови силових багатокутників при визначенні реакцій за рівняннями (3.16) та (3.25) можуть бути різними. 3.1.14. Величина реакції дії опори на першу ланку:
де μр – масштаб побудови, Н/мм.
Рисунок 3.6 – Векторний багатокутник
12 |




 та
та  , сили інерції другої та третьої ланок
, сили інерції другої та третьої ланок  та
та 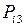 , сила опору
, сила опору  , реакція опори на третю ланку
, реакція опори на третю ланку  , реакція дії першої ланки на другу з нормальною
, реакція дії першої ланки на другу з нормальною  і тангенціальною
і тангенціальною  складовими (рис. 3.2).
складовими (рис. 3.2).
 . Сили інерції
. Сили інерції  та
та 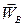 відповідно, сила опору
відповідно, сила опору  швидкості точки В.
швидкості точки В. містить у собі дві складові: нормальну
містить у собі дві складові: нормальну  проходить через точку В і спрямована вертикально (вгору або вниз).
проходить через точку В і спрямована вертикально (вгору або вниз). , (3.1)
, (3.1) – динамічний момент, Н∙м;
– динамічний момент, Н∙м; – момент інерції мас другої ланки відносно центру ваги, кг∙м2:
– момент інерції мас другої ланки відносно центру ваги, кг∙м2: . (3.2)
. (3.2) ; (3.3)
; (3.3) , (3.4)
, (3.4) ; (3.5)
; (3.5) , (3.6)
, (3.6) , аВ – прискорення центру ваги другої ланки та прискорення повзуна відповідно, м/с2;
, аВ – прискорення центру ваги другої ланки та прискорення повзуна відповідно, м/с2; – сили інерції другої та третьої ланок відповідно, Н.
– сили інерції другої та третьої ланок відповідно, Н.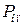 необхідно побудувати діаграму навантаження (рис. 3.3). Діаграма має вигляд паралелограма і будується під планом механізму або над ним: крайній лівий кут паралелограма – під крайнім лівим положенням повзуна (на рис. 3.3 точка В6), а крайній правий кут – під крайнім правим положенням повзуна (точка В0). При цьому відстань ОSmax на діаграмі відповідає відстані В0В6 між двома крайніми положеннями повзуна механізму.
необхідно побудувати діаграму навантаження (рис. 3.3). Діаграма має вигляд паралелограма і будується під планом механізму або над ним: крайній лівий кут паралелограма – під крайнім лівим положенням повзуна (на рис. 3.3 точка В6), а крайній правий кут – під крайнім правим положенням повзуна (точка В0). При цьому відстань ОSmax на діаграмі відповідає відстані В0В6 між двома крайніми положеннями повзуна механізму. , МПа/мм. (3.7)
, МПа/мм. (3.7)
 , Н (3.8)
, Н (3.8) , Н, (3.9)
, Н, (3.9) , МПа; (3.10)
, МПа; (3.10) , мм2 (3.11)
, мм2 (3.11) ,
,  ; (3.12)
; (3.12) , (3.13)
, (3.13) ,
,  та
та  – плечі відповідних сил, мм (перпендикуляри з точки В до лінії дії сили, їх довжини вимірюються на листі).
– плечі відповідних сил, мм (перпендикуляри з точки В до лінії дії сили, їх довжини вимірюються на листі). , Н. (3.14)
, Н. (3.14) ; (3.15)
; (3.15) . (3.16)
. (3.16) , що був визначений раніше. Далі, враховуючи масштаб μр, проводимо всі наступні вектори у порядку, вказаному в рівнянні рівноваги (3.16). Вектор реакції
, що був визначений раніше. Далі, враховуючи масштаб μр, проводимо всі наступні вектори у порядку, вказаному в рівнянні рівноваги (3.16). Вектор реакції  знайдемо як суму векторів
знайдемо як суму векторів 
 , Н; (3.17)
, Н; (3.17) , Н, (3.18)
, Н, (3.18) та
та 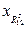 – довжини векторів з багатокутника, мм;
– довжини векторів з багатокутника, мм; , Н. (3.19)
, Н. (3.19) , реакція дії опори на першу ланку
, реакція дії опори на першу ланку  , реакція дії другої ланки на першу
, реакція дії другої ланки на першу 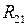 та зрівноважувальна сила
та зрівноважувальна сила  (рис. 3.5).
(рис. 3.5).
 . Зрівноважувальна сила
. Зрівноважувальна сила  , Н. (3.20)
, Н. (3.20) ; (3.21)
; (3.21) , (3.22)
, (3.22) та
та  – плечі зрівноважувальної сили та реакції дії другої ланки на першу відповідно, мм.
– плечі зрівноважувальної сили та реакції дії другої ланки на першу відповідно, мм. , Н. (3.23)
, Н. (3.23) ; (3.24)
; (3.24) . (3.25)
. (3.25) , (3.26)
, (3.26)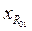 – довжина вектора реакції R01 з багатокутника, мм;
– довжина вектора реакції R01 з багатокутника, мм;