 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Кінематичний аналіз механізму 12
I ЧАСТИНА Дослідження важільного механізму Проводиться дослідження плоского важільного кривошипно-шатунного (кривошипно-повзунного) механізму. Структурний аналіз механізму
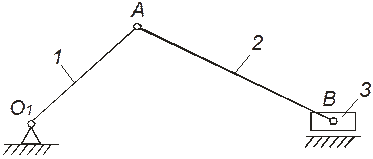
1 – кривошип; 2 – шатун; 3 – повзун Рисунок 1.1 – Умовнасхема механізму
Заданий кривошипно-шатунний механізм складається з трьох рухомих ланок (1,2,3) та однієї нерухомої ланки (корпуса, або стояка). Ланки з’єднані між собою за допомогою кінематичних пар V класу. Ступінь рухомості W даного механізму визначається за формулою П. Чебишева:
де n – кількість рухомих ланок, n=3; р5, р4 – кількість кінематичних пар V та IV класів відповідно, р5=4, р4=0. Після підстановки значень одержимо:
W=1 означає, що даний механізм має тільки одну ведучу ланку.
Кінематичний аналіз механізму Кінематичний аналіз важільного механізму включає: - побудову плану положень механізму у 12-ти положеннях; - побудову плану швидкостей механізму у двох довільних положеннях; - побудову плану прискорень механізму у двох довільних положеннях.
2.1 Побудова плану положень механізму
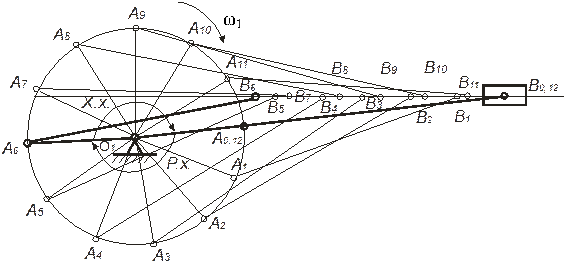
План положень механізму (план механізму) – це відображення кінематичної схеми механізму у вибраному масштабі, що відповідає заданим положенням ведучої ланки. 2.1.1. Для побудови плану положень механізму спочатку проводимо горизонтальну лінію, на якій довільно вибираємо точку механізму O1 (рис. 2.1). 2.1.2. Вертикально вгору від точки O1 відкладаємо відстань YB (з умови завдання) і проводимо ще одну горизонтальну лінію, яка відповідає траєкторії руху повзуна (поршня). 2.1.3. З точки O1 радіусом (O1А+АВ) проводимо коло до перетину з лінією траєкторії руху повзуна. Отримана точка перетину В0 є крайнім положенням повзуна. 2.1.4. З’єднуємо точки O1 та В0. 2.1.5. З точки O1 радіусом O1А проводимо коло – траєкторію руху точки А кривошипа. На перетині кола з лінією O1В0 отримаємо точку А0. Лінія, що проходить через точки O1, А0 та В0, показує механізм у крайньому (або нульовому) положенні. Тут повзун займає найбільш віддалене положення, а кривошип та шатун розташовані на одній лінії (див. рис. 2.1). 2.1.6. Для побудови плану механізму у дванадцяти положеннях поділимо коло на 12 рівних частин (кожна по 30º). Відкладаємо кут 30º від O1А0 у напрямку кутової частоти обертання кривошипа ω1 (напрям задається викладачем) і на лінії кола одержуємо точку А1. Проводимо радіус O1А1 і з точки А1 колом радіуса АВ перетинаємо лінію траєкторії руху повзуна. Отримана точка B1 показує перше положення повзуна. Таким чином будується перше положення механізму. Друге та наступні положення механізму будуються аналогічно першому, починаючи з точок А2, А3, …і до А11. Слід зауважити, що дванадцяте положення та нульове співпадають між собою.
Рисунок 2.1 – Схема побудови плану положень механізму
2.1.7. Після побудови усього плану механізму визначимо робочий та холостий хід механізму. Вважається, що робочому ходу відповідає більший кут повороту кривошипа між двома його крайніми положеннями. Тоді менший кут повороту кривошипа між двома крайніми положеннями відповідає холостому ходу (рис. 2.2).
Рисунок 2.2 – Визначення робочого ходу та холостого ходу механізму
2.2 Побудова планів швидкостей
Побудуємо план швидкостей для одного з положень ланок механізму при робочому ході. Візьмемо для прикладу перше положення (рис.2.3). Спочатку проводяться необхідні розрахунки. 2.2.1. Кутова швидкість першої ланки – кривошипа:
де n1 – частота обертання двигуна, об/хв. (з умови завдання). 2.2.2. Лінійна швидкість точки А (направлена завжди з точки А по дотичній до кола у цій точці, тобто перпендикулярно до ланки О1А, рис. 2.3):
Рисунок 2.3 – Механізм у першому положенні
2.2.3. Беремо довільну точку р на площині (полюс) та проводимо з неї вектор ра перпендикулярно до ланки О1А1 у даному положенні механізму. Довжина відрізка ра береться довільна (довжиною ≥ 80 мм). Одержали вектор швидкості точки А – 2.2.4. Масштаб плану швидкостей:
2.2.5. Для побудови векторів швидкостей ланок 2 та 3 використовуються наступні умови: 1) 2) 2.2.6. Вектор
Рисунок 2.4 – План швидкостей для першого положення
2.2.7. Для знаходження вектора швидкості центру ваги S2 необхідно відкласти на відрізку ав відстань аS2, що визначається, як 2.2.8. Величини векторів швидкостей знаходяться за формулами:
Аналогічно будується план швидкостей для всіх інших положень механізму. 2.2.9. Кутова швидкість другої ланки – шатуна АВ:
Довжину 2.2.10. Напрям вектора ω2 визначається таким чином: якщо умовно перенести вектор
Рисунок 2.5 – Ілюстрація до пункту 2.2.10
2.3 Побудова планів прискорень
Продовжимо розглядати перше положення механізму (О1А1В1). 2.3.1. Прискорення точки А:
Нормальне прискорення точки А:
Тангенціальне (дотичне) прискорення точки А:
Оскільки кутове прискорення кривошипа Тоді прискорення точки А:
2.3.2. Для побудови плану прискорень беремо довільну точку π (полюс) і у напрямку від точки А1 до О1 проводимо лінію πа (довжиною не менше 80 мм). Одержали вектор прискорення точки А – 2.3.3. Масштаб плану прискорень:
2.3.4. Прискорення точки В: 1) 2) 2.3.5. Нормальне прискорення ланки 2:
Враховуючи масштаб плану прискорень μw, нормальне прискорення ланки 2:
2.3.6. З точки а проводимо вектор 2.3.7. Вектор тангенціального прискорення
Рисунок 2.6 – План прискорень для першого положення
2.3.8. Для знаходження вектора прискорення центру ваги S2 потрібно з’єднати точки а та в пунктирною лінією та відкласти від точки а відстань аS2, що визначається, як 2.3.9. Величини векторів прискорень розраховуються за формулами:
Аналогічним чином будується план прискорень для другого та наступних положень механізму. 2.3.10. Кутове прискорення другої ланки АВ:
Довжину 2.3.11. Напрям вектора
Рисунок 2.7 –Ілюстрація до пункту 2.3.11
Кінетостатичний аналіз
12 |



 , (1.1)
, (1.1) .
.
 , рад/с, (2.1)
, рад/с, (2.1) , м/с. (2.2)
, м/с. (2.2)
 (рис 2.3).
(рис 2.3). . (2.3)
. (2.3)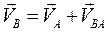 ;
; (повзун рухається горизонтально).
(повзун рухається горизонтально). проводимо з точки а перпендикулярно до ланки А1В1, до перетину з горизонтальною лінією, яка проходить через полюс. Одержимо точку в. Вектори в точці в сходяться. У результаті отримаємо вектори швидкостей ланки ВА та точки В повзуна –
проводимо з точки а перпендикулярно до ланки А1В1, до перетину з горизонтальною лінією, яка проходить через полюс. Одержимо точку в. Вектори в точці в сходяться. У результаті отримаємо вектори швидкостей ланки ВА та точки В повзуна –  відповідно (рис. 2.4).
відповідно (рис. 2.4).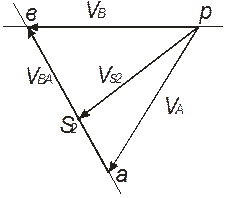
 . Величина ab вимірюється у міліметрах (з плану швидкостей), величина
. Величина ab вимірюється у міліметрах (з плану швидкостей), величина  – з умови завдання. Провівши вектор з полюса до точки S2, отримаємо вектор швидкості центру ваги
– з умови завдання. Провівши вектор з полюса до точки S2, отримаємо вектор швидкості центру ваги  (див. рис. 2.4).
(див. рис. 2.4). , м/с; (2.4)
, м/с; (2.4) , м/с; (2.5)
, м/с; (2.5) , м/с. (2.6)
, м/с. (2.6) , рад/с. (2.7)
, рад/с. (2.7) потрібно брати у метрах.
потрібно брати у метрах.
 (2.8)
(2.8) , м/с2. (2.9)
, м/с2. (2.9) , м/с2. (2.10)
, м/с2. (2.10) , то
, то  .
. . (2.11)
. (2.11)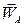 .
. . (2.12)
. (2.12) ;
; (повзун рухається горизонтально).
(повзун рухається горизонтально). , м/с2. (2.13)
, м/с2. (2.13) . (2.14)
. (2.14) довжиною, одержаною за формулою (2.14). Отримаємо точку τ (рис. 2.6).
довжиною, одержаною за формулою (2.14). Отримаємо точку τ (рис. 2.6). проводимо з точки τ перпендикулярно до вектора нормального прискорення
проводимо з точки τ перпендикулярно до вектора нормального прискорення  , до перетину з горизонтальним вектором прискорення точки В
, до перетину з горизонтальним вектором прискорення точки В 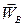 , який проходить через полюс. Одержимо точку в. Вектори прискорень у точці в сходяться.
, який проходить через полюс. Одержимо точку в. Вектори прискорень у точці в сходяться.
 (див. рис. 2.6).
(див. рис. 2.6). , м/с2; (2.15)
, м/с2; (2.15) , м/с2; (2.16)
, м/с2; (2.16) , м/с2. (2.17)
, м/с2. (2.17) , рад/с2. (2.18)
, рад/с2. (2.18) визначається таким чином: якщо умовно перенести вектор
визначається таким чином: якщо умовно перенести вектор 