 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Определение срока ссуды и величины процентной ставки
Для расчета срока ссуды и величины процентной ставки по кредиту используются следующие формулы:
Пример 4: В контракте предусматривается погашение обязательства в сумме 12000 руб. через 300 дней. Первоначальная сумма долга 10 000 руб. Определить доходность ссудной операции в виде простой годовой ставки наращения при К = 360.
Пример 5. Какова должна быть продолжительность ссуды в днях для того, чтобы долг равный 9000 руб., вырос до 10000 руб. при условии, что простая ставка наращения равна 18,5% годовых при К = 365?
Сложная процентная ставка наращения Сложная процентная ставка наращения – это ставка, при которой база начисления является переменной, т.е. проценты начисляются на проценты.
Пример 6. Какой величины достигнет долг, равный 6000 руб. через 4 года при росте по сложной ставке наращения 18,5% годовых?
Пример 7. Какой величины достигнет долг, равный 8000 руб. через 4,6 года при росте по сложной ставке наращения 20% годовых?
Номинальная ставка наращения. Часто в финансовых операциях в качестве периода наращения процентов используется не год, а месяц, квартал или другой период. В этом случае говорят, что проценты начисляются mраз в году. В контрактах обычно фиксируется не ставка за период, а годовая ставка, которая в этом случае называется номинальной.
Пример 8. Какой величины достигнет долг, равный 15000 руб. через 5,7 года при росте по сложной ставке наращения 16,5% годовых при начислении процентов раз в году и помесячно?
Расчет наращенных сумм в условиях инфляции
В целях уменьшения воздействия инфляции и компенсации потерь от снижения покупательной способности денег используются различные методы. Один из них – индексация процентной ставки. Сущность его в том. Что процентная ставка корректируется в соответствии с темпом инфляции. Ставку, скорректированную на инфляцию, условно можно назвать брутто-ставкой (
где In – индекс инфляции; n – срок кредита; i- номинальная процентная ставка.
Пример 9. Банк выдал на 6 месяцев кредит – 0,5 млн. руб. Ожидаемы месячный уровень инфляции – 2%, требуемая реальная доходность операции равна 10% годовых. Определить ставку процентов по кредиту с учетом инфляции, размер наращенной суммы и величину процентного платежа.
При выдаче долгосрочных кредитов сложная процентная ставка, обеспечивающая при годовом уровне инфляции
Пример 10. Кредит в 1,5 млн руб выдан на 2 года. Реальная доходность должна составлять 11% годовых (сложные проценты). Расчетный уровень инфляции 16% в год. Определить ставку процентов при выдаче кредита, а также наращенную сумму.
В случае, когда применяется величина индекса инфляции за весь срок кредита, процентная става, учитывающая инфляцию, определяется по формуле:
Пример 11. Кредит 2 млн руб выдан на 3 года. На этот период прогнозируется рост цен 1,5 раза. Определить ставку процентов при выдаче кредита и наращенную сумму долга, если реальная доходность должна составлять 12% по ставке сложных процентов.
Консолидация платежей
Изменение хозяйственной ситуации нередко побуждает одну из сторон-участниц коммерческой сделки обратиться к другой стороне с предложением изменить условия ранее заключенных соглашений. Наиболее часто предлагается: изменить сроки платежей в один (консолидировать платежи) с установлением единого срока погашения и т.п. Естественно, что предлагаемые изменения должны быть безубыточны для обеих сторон , т.е. основным принципом изменения условия сделки (контракта) является принцип финансовой эквивалентности. Для решения таких задач используется уравнение эквивалентности, в котором сумма заменяемых платежей, приведенных к одному моменту времени, приравнена к сумме платежей по новому обязательству, приведенной к той же дате. При консолидации нескольких платежей в один при условии, что срок нового консолидированного платежа больше ранее установленных сроков, т.е. n0 >n1, n2, …..nj, уравнение эквивалентности имеет вид:
где S0 – наращенная сумма консолидированного платежа; S1, S2,….Sj – платежи, подлежащие консолидации, со сроками уплаты n1, n2…nj; tj- временные интервалы между сроком n0 и nj, т.е. tj = n0-nj. Рассмотрим использование данного уравнения. Задача 12. Фирма получила кредит на сумму 900тыс.руб под 10% годовых (простые проценты). Кредит должен быть погашен двумя платежами: первый – 500 тыс. руб. с процентами через 90 дней, второй – 400 тыс. руб. с процентами через 120 дней. Впоследствии фирма договорилась с кредитором об объединении платежей в один со сроком погашения через 150 дней. Необходимо определить размер консолидированного платежа (К=360).
Суммы, подлежащие возврату на старых условиях:
Сумма погашения консолидированного платежа будет равна:
Так как принцип эквивалентности состоит в том, что первоначальная сумма Р в начале периода эквивалентна платежу S в конце периода, то дисконтированная сумма консолидированного платежа на момент предоставления кредита должна быть равна сумме полученного кредита:
Объединение платежей может производиться на условиях, предусматривающих разные сроки выплаты консолидированного платежа. Поэтому в общем случае величину консолидированного платежа определяют по формуле:
где Sj- суммы объединенных платежей, сроки погашения которых меньше нового срока nj<n0; Sk – суммы объединяемых платежей со сроками, превышающими новый срок, nk>n0 Соответственно, tj = n0-nj, tk = nk-n0. Задача 13. Фирма в погашение задолженности банку за предоставленный под 15% годовых (простые проценты) кредит, полученный 01.01, должна произвести три платежа – 200 тыс. руб.; 270 тыс. руб. и 330 тыс. руб. в сроки 20.04, 25.05, 15.06. Фирма предложила банку объединить все платежи в один и погасить его 01.06. (К=365) Определите величину консолидированного платежа.
При консолидации платежей с использованием сложной процентной ставки применяется следующая формула:
Задача 14. Два платежа
Вопрос о консолидации платежей можно решить и по другому принципу: партнеры заранее обусловливают сумму консолидированного платежа, при этом необходимо рассчитать срок его уплаты, сохраняя при этом принцип эквивалентности, Срок уплаты консолидированного платежа определяется по формуле:
где S0- сумма консолидированного платежа; Р0 – современная величина консолидируемых платежей; i- процентная ставка, используемая при консолидации.
Задача 15. Фирма имеет ряд финансовых обязательств перед одним кредитором – 2,5 млн. руб, 3,1 млн руб, 2,7 млн руб, которые должна погасить через 40, 70 и 160 дней после 01.01 текущего года. По согласованию сторон решено заменить их одним платежом, равным 9 млн руб., с продлением срока оплаты, используя процентную ставку i=12%. (К=365) Необходимо найти срок уплаты консолидированного платежа.
Современная величина (Р0) объединяемых платежей составит :
В случае договоренности партнеров о консолидации платежей без изменения общей суммы платежа, т.е. S0=∑ Sj, срок консолидированного платежа рассчитывается по формуле:
Задача 16. Платежи в размере 2,5 млн руб., 3,1 млн руб и 2,7 млн. руб. должны быть внесены 40, 70 и 160 дней после 01.01 текущего года. Достигнуто соглашение на объединение этих платежей без увеличения итоговой суммы, т.е. S0=∑ Sj. Определите срок уплаты консолидированного платежа.
Потоки платежей Потоки платежей – это последовательные во времени платежи, например, пенсии, выплаты по купонам облигаций и т.д. Характеристики потоков платежей:: - регулярным потоком платежей (финансовой рентой) называются платежи, у которых выплаты постоянны, происходят по установленным правилам и интервалы между платежами одинаковы; По моменту выплат в пределах периода между платежами ренты делятся на: - постнумерандо (выплаты производятся в конце периода); - пренумерандо (выплаты производятся в начале периода); - ренты с платежами в середине периода. Наращенная сумма потока платежей – это сумма всех выплат с начисленными на них к концу срока сложными процентами. Современная стоимость потока платежей – это сумма всех выплат, дисконтированных на начало срока этого потока по сложной процентной ставке. Наращенная сумма такого потока платежей рассчитывается по формуле:
Современная стоимость потока платежей определяется соотношением:
Задача 17. Имеется следующий график платежей во времени: 1 января 2011 г – 20 000 руб 1 июля 2011 г – 30 000 руб 1 января 2012 г – 10 тыс руб 1 января 2013 г – 40 тыс руб Определите сумму задолженности на 1 января 2013 г и ее современную стоимость на момент выплаты первой суммы при ставке наращения 15% годовых.
Современная стоимость потока платежей составит:
Постоянная рента Годовая рента Годовая рента постнумерандо предусматривает выплаты и начисление процентов один раз в конце года. Наращенная сумма годовой ренты концу срока вычисляется по формуле:
Задача 18. В фонд ежегодно в конце года поступают средства по 10 000 рублей в течение 7 лет, на которые начисляются проценты по ставке 15% годовых. Определите величину фонда на конец срока.
|
).
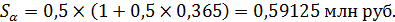
, реальную эффективность кредитной операции, определяется по формуле
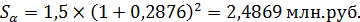
= 20.04 - 01.06= 42 дня,
= 7 дней,
= 14 дней.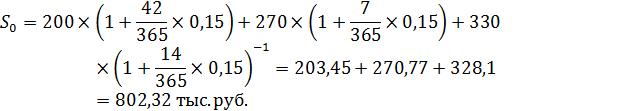
= 1,7 млн руб и 
= 1,3 млн руб. со сроками погашения 1 год 30 дней и 1 год 45 дней, отсчитываемыми от одной даты, заменяются одним платежом со сроком 1 год 75 дней. Стороны согласились на консолидацию платежей при использовании ставки сложных процентов 9% годовых. Определите сумму консолидированного платежа. (к=365)
