 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Прерывисто контактны режим работы
В бесконтактном режиме кантилевер совершает вынужденные колебания с малой амплитудой порядка 1 нм. При приближении зонда к поверхности на кантилевер начинает действовать дополнительная сила со стороны образца FPS/ При ван-дер-вальсовом а взаимодействии это соответствует области расстояний между зондом и образцом, где действует сила притяжения. Если зонд АСМ находится на расстоянии z0 от поверхности, то для малых колебаний можно записать:
Это приводит к тому, что в правой части уравнения, описывающего колебания в такой системе, появляются дополнительные слагаемые:
Вводя новые переменные:
Т.е. наличие градиента сил приводит к изменению эффективной жесткости системы:
После стандартных преобразований уравнение записывается в следующем виде:
Производя вычисления, аналогичные вычислениям, проведенным для свободного кантилевера, получаем амплитудно-частотную характеристику системы:
И, соответственно, ФЧХ:
Таким образом, наличие градиента силы взаимодействия зонда с поверхностью образца приводит к дополнительному сдвигу АЧХ и ФЧХ системы. Резонансная частота в присутствии внешней силы ωrf может быть представлена в виде
Следовательно, дополнительный сдвиг АЧХ равен
Из выражения (9) также следует, что наличие градиента силы приводит к сдвигу ФЧХ, так что точка ее перегиба ω* находится на частоте
Пусть кантилевер вдали от поверхности совершает вынужденные колебания на частоте поверхностью фаза колебаний (считаем
Следовательно, дополнительный сдвиг фазы при наличии градиента силы будет равен [35]:
Он определяется производной z-компоненты силы по координате z. Данное обстоятельство используется для получения фазового контраста в АСМ исследованиях поверхности.
Регистрация изменения амплитуды и фазы колебаний кантилевера в бесконтактном режиме требует высокой чувствительности и устойчивости работы обратной связи. На практике чаще используется так называемый "полуконтактный" режим колебаний кантилевера (иногда его называют прерывисто-контактный, а в иностранной литературе - "intermittent contact" или "tapping mode" режимы). При работе в этом режиме возбуждаются вынужденные колебания кантилевера вблизи резонанса с амплитудой порядка 10 – 100 нм. Кантилевер подводится к поверхности так, чтобы в нижнем полупериоде колебаний происходило касание поверхности образца (это соответствует области отталкивания на графике зависимости силы от расстояния (рис. 82)). При сканировании образца регистрируется изменение амплитуды и фазы колебаний кантилевера. Взаимодействие кантилевера с поверхностью в "полуконтактном" режиме состоит из ван-дер-ваальсового взаимодействия, к которому в момент касания добавляется упругая сила, действующая на кантилевер со стороны поверхности. Если обозначить через z0 расстояние между положением равновесия колеблющегося кантилевера и поверхностью, а через )) -
где координата z отсчитывается от поверхности. Заметим, что "полуконтактный" режим реализуется только тогда, когда расстояние z0 меньше амплитуды колебаний кантилевера:
Теория "полуконтактного" режима значительно сложнее теории бесконтактного режима, поскольку в этом случае уравнение, описывающее движение кантилевера, существенно нелинейно. Сила взаимодействия поверхности и зонда в нижней точке колебаний кантилевера. Поскольку в нижней точке колебаний зонд механически взаимодействует с поверхностью, то на изменение амплитуды и фазы колебаний кантилевера в этом режиме существенное влияние оказывает локальная жесткость поверхности образцов. Сдвиг по фазе между колебаниями возбуждающего пьезоэлектрического вибратора и установившимися колебаниями кантилевера можно оценить, если рассмотреть процесс диссипации энергии при взаимодействии зонда с образцом [36-38]. При установившихся колебаниях энергия, приходящая в систему, в точности равна энергии, рассеиваемой системой. Энергия, поступающая в систему от пьезовибратора за период колебаний:
Она расходуется на восполнение потерь при взаимодействии кантилевера с атмосферой и образцом. Энергию EPA рассеиваемую в атмосферу за период, можно вычислить следующим образом:
Энергия EPS идущая на восполнение потерь при диссипативном взаимодействии зонда с образцом, равна:
Из условия баланса следует:
Предполагая, что установившиеся колебания кантилевера имеют вид Отсюда для фазового сдвига получается следующее выражение:
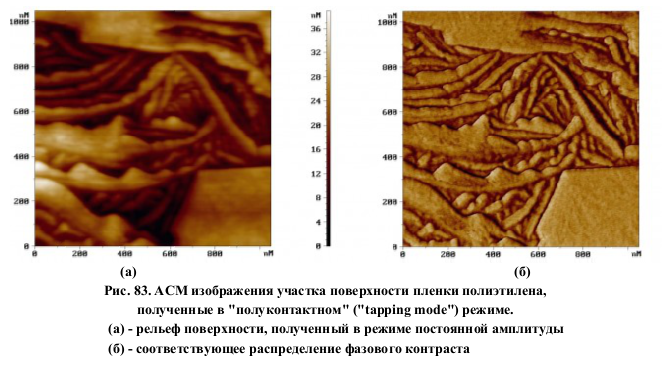
Таким образом, фазовый сдвиг колебаний кантилевера в "полуконтактном" режиме определяется энергией диссипативного взаимодействия зонда с поверхностью образца. Формирование АСМ изображения поверхности в режиме колебаний кантилевера происходит следующим образом. С помощью пьезовибратора возбуждаются колебания кантилевера на частоте ω (близкой к резонансной частоте кантилевера) с амплитудой Аω. При сканировании система обратной связи АСМ поддерживает постоянной амплитуду колебаний кантилевера на уровне A0 , задаваемом оператором (A0 < Аω). Напряжение в петле обратной связи (на z-электроде сканера) записывается в память компьютера в качестве АСМ изображения рельефа поверхности. Одновременно при сканировании образца в каждой точке регистрируется изменение фазы колебаний кантилевера, которое записывается в виде распределения фазового контраста. На рис. 83, в качестве примера, приведены АСМ изображения участка пленки полиэтилена, полученные в "полуконтактном" режиме (амплитудный и фазовый контраст).
Практическая часть
Выводы
Литература 1. G.Binnig, C.F.Quate, Ch.Gerber – Atomic force microscope. // Phys. Rev. Lett., v. 56, № 9, p. 930 – 933 (1986).
|
приходим к уравнению:
0, тогда сдвиг фазы его колебаний составляет π/2. При сближении с
) станет равной
комбинированную силу, то уравнение движения кантилевера можно записать в следующем виде:
, получаем:
Результирующий профиль при усреднении 128 измерений. Высота ступеньки составляет 6,87±0,3 нм 
Полуконтактный метод измерения 
Результирующий профиль при усреднении 128 измерений. Высота ступеньки составляет 20,5±0,3 нм 
Поиск объекта измерения – чувствительной части фотодетектора. 
Измрение геометрических характеристик фотодатчика. 
В первом столбце – номер линии Во втором – разность высот между начальной и конечной точкой линии N N Δz [nm] 1 7,7 2 7,7 3 65,9 4 12,3 5 140,3 6 215,0 7 231,4 8 141,3