 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Теорема. Всякое бесконечное множество содержит счетное подмножество. 12
Доказательство. Пусть M - бесконечное множество. Тогда
и можно выбрать элемент
Он отличен от всех ранее выбранных элементов. По принципу индукции доказано, что для любого n существует в M подмножество An = {a1, a2, ..., an} из n элементов, причем множество An+1 получается из An присоединением одного нового элемента an+1. Очевидно, что объединение
является счетным подмножеством M. Теорема о мощности множества рациональных чисел. Теорему хз, но множество рациональных чисел есть счетное множество 4. Теорема. Отрезок [0,1] есть бесконечное несчетное множество. http://fan-5.ru/best/best-187892.php 5. Теорема 1. Последовательность точек расширенной числовой прямой
Теорема о связи бесконечно больших и бесконечно малых последовательностей. Предел частного (отношения) двух бесконечно малых или бесконечно больших величин не изменится, если одну из них (или обе) заменить эквивалентной величиной. Данная теорема имеет прикладное значение при нахождении пределов 7. 8. Свойства пределов: 1. Предел сonst равен сonst 2. Постоянный множитель c можно выносить за знак предела:
3. Предел произведения последовательностей равен произведению пределов последовательности. 4. Для того чтобы {Xn} сходилось к «а», необходимо и достаточно, чтобы Xn=a+αn(n→0)а Xn→а 5. Алгебраическая сумма\разность сходящихся последовательностей есть сходящаяся последовательность и ее предел равен сумме\разности пределов данной последовательности 6. Если {Xn} и {Yn} сходятся, а предел {Xn} равен аипредел {Yn} равенв(n→∞) Причем{Yn≠0} ив≠0, то{Xn\Yn}сходящиеся и предел от{Xn\Yn}=а\в
Теорема о переходе к пределу в неравенствах Пусть заданы две последовательности Док-во Yn-Xn≥0 (т.к. Xn≤Yn ) lim(Yn-Xn)=limYn-limXn≥0приn→∞ Теорема о 2х милиционерах
Условие позволяет предположить, что для любого существует окрестность , в которой верны
12 |



 . выберем какой-нибудь из его элементов и обозначим его через a1. Пусть в M уже выбраны n различных между собою элементов a1, a2, ..., an. Так как M бесконечно, то
. выберем какой-нибудь из его элементов и обозначим его через a1. Пусть в M уже выбраны n различных между собою элементов a1, a2, ..., an. Так как M бесконечно, то





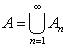


 может иметь на этой прямой только один предел.
может иметь на этой прямой только один предел.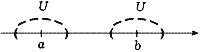 Рис. 49
Рис. 49 Допустим противное. Пусть существует такая последовательность xn
Допустим противное. Пусть существует такая последовательность xn 
 = a и
= a и  b, a
b, a  V =
V =  . Согласно определению предела вне окрестности U точки а, в частности в окрестности Vточки b, содержится лишь конечное число членов последовательности {xn}. Однако точка b также является ее пределом, и потому в ее окрестности V должны находиться все члены последовательности {xn}, начиная с некоторого номера, а следовательно, бесконечно много ее членов. Получилось противоречие.
. Согласно определению предела вне окрестности U точки а, в частности в окрестности Vточки b, содержится лишь конечное число членов последовательности {xn}. Однако точка b также является ее пределом, и потому в ее окрестности V должны находиться все члены последовательности {xn}, начиная с некоторого номера, а следовательно, бесконечно много ее членов. Получилось противоречие. 

 и
и  . Если
. Если  и, начиная с некоторого номера,
и, начиная с некоторого номера,  , то выполняется неравенство:
, то выполняется неравенство: 
 Если функция такая, что
Если функция такая, что  для всех
для всех  в некоторой окрестности точки
в некоторой окрестности точки  , причем функции
, причем функции  и
и  имеют одинаковый предел при
имеют одинаковый предел при  , то существует предел функции
, то существует предел функции 
 неравенство . Тогда верно
неравенство . Тогда верно неравенство .
неравенство .

 неравенства и . Из изложенной выше оценки
неравенства и . Из изложенной выше оценки
 максимумом следует, что при , что удовлетворяет
максимумом следует, что при , что удовлетворяет
 определению предела, то есть
определению предела, то есть