 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Теорема «Мощность декартова произведения конечных множеств» 12
Пределы I) Определения Множество - совокупность различных элементов, мыслимую как единое целое Пусто́емно́жество— множество, не содержащее ни одного элемента.Пустое множество является конечным множеством и имеет наименьшую мощность среди всех множеств. Подмножество- Множество Сумма множеств- множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств Разность множеств- (А-В) множество элементов А не входящие в множество В. Прямое произведение множеств– множество элементов всевозможно упорядоченных пар Фу́нкция (отображе́ние)— математическое понятие, отражающее однозначную парную связь элементов одного множества с элементами из другого множества. Иньекция – элементы противопоставлены разным элементам Сюрьекция – противопоставлено может быть и нескольким Биекция – один к одному, каждому элементу свой элемент Взаимно-однозначное соответствие- биективное отображение Эквивалентные множества– соответствие одного множества другому. Равномощные множества- множества, содержащие равное кол-во элементов. Счетное множество– множество, элементы которого можно пронумеровать натуральными числами. Множество мощности континуума– (несчетное множество) –точно максимальная мощность?! - хз Инфинум – наибольший элемент Супремум – Другими словами, супремум — это наименьшая из всех верхних граней. Обозначается Последовательность – набор элементов некоторого множества. Предел последовательности - Поэтому, число Последовательность Последовательность Сходящаяся последовательность — это последовательность элементов множества Расходящаяся последовательность— это последовательность, не являющаяся сходящейся.
Сумма, разность, произведение и частное последовательностей- Суммой числовых последовательностей Разностью числовых последовательностей Произведением числовых последовательностей Частным числовой последовательности
Ограниченная последовательность- последовательность ограниченная сверху, снизу, сверху и снизу. Это значит элементы не превышают некоторый элемент\число. Возраст, убыв, неубывающие, невозрастающие– Пусть имеется множество Последовательность
Последовательность
Последовательность
Последовательность
Монотонные последовательности– Последовательность называется монотонной, если она является неубывающей, либо невозрастающей Предел функции–
Односторонние пределы - предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́ннимпреде́лом (или преде́ломсле́ва) и правосторо́ннимпреде́лом (преде́ломспра́ва). Предел справа - Число
Предел слева - Число
Бесконечно малая функция – функция стремящаяся к 0 Бесконечно малая функция одного порядка - Если
Бесконечно малая функция более высокого порядка - Если Несравнимые бесконечно малые –Если не существует, предела то α(x) и β(x) называются несравнимыми бесконечно малыми функциями. Эквивалентные бесконечно малые - Если Очевидно, что эквивалентные величины являются частным случаем бесконечно малых (бесконечно больших) величин одного порядка малости. Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции Непрерывная функция в точке –Если предел функции слева равен пределу справа и равен функции Если для любого ε>0 существует б>0 : |f(x)-f(x0)|<ε для любого x:|x-x0|<б Функция непрерывная справа – Функция непрерывная слева – Функция непрерывная на интервале –f(x) непрерывна на (a,b), если она непрерывна в каждой точке этого интервала. Функция непрерывная на отрезке –f(x) непрерывна на отрезке [a,b] если она непрерывна на интервале (a,b), и непрерывна справа в точке и слева в точке b. Точки разрыва –Если условие, входящее в определение непрерывности функции, в некоторой точке нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Точка разрыва 1-го рода –если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода. К точкам разрыва первого рода относят устранимые разрывы и скачки. Точка разрыва 2-го рода –если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода. К точкам разрыва второго рода относят полюса и точки существенного разрыва. Устранимый разрыв –Если предел функции существует и конечен, но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке: то точка Если «поправить» функцию
Ii) Теоремы
Теорема «Мощность декартова произведения конечных множеств» Два конечных множества равномощны тогда и только тогда, когда они состоят из одинакового числа элементов. То есть для конечного множества понятие мощности совпадает с привычным понятием количества. | А1|=m1…| Аn |=mn | А1×…×Аn |= m1*...*mn 1)n=1 | А1|=m1 2) Пусть теорема верна при n=k Докажем для n=k+1 | А1×…×Аk |= m1*...*mk | А1×…×Аk+1 |= (m1*...*mk )mk+1 12 |



 является подмножеством множества
является подмножеством множества  , если любой элемент, принадлежащий
, если любой элемент, принадлежащий  , но иногда можно встретить запись в виде суммы
, но иногда можно встретить запись в виде суммы  .
. , который равен или меньше всех элементов множества
, который равен или меньше всех элементов множества  . Другими словами, инфимум — это наибольшая из всех нижних граней.
. Другими словами, инфимум — это наибольшая из всех нижних граней. .
. называется пределом последовательности
называется пределом последовательности  , если для любого
, если для любого  существует номер
существует номер  , зависящий от
, зависящий от  такой, что для любого
такой, что для любого  выполняется неравенство
выполняется неравенство  .
. называется бесконечно малой, если
называется бесконечно малой, если 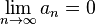 Например, последовательность чисел
Например, последовательность чисел  — бесконечно малая.
— бесконечно малая. .
. и
и  называется числовая последовательность
называется числовая последовательность  такая, что
такая, что  .
. .
.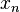 и
и  называется числовая последовательность
называется числовая последовательность  .
. . Если в последовательности
. Если в последовательности  всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность
всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность  .
.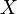 , на котором введено отношение порядка.
, на котором введено отношение порядка. элементов множества
элементов множества 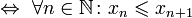
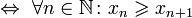




 называется правосторонним пределом (правым пределом, пределом справа) функции
называется правосторонним пределом (правым пределом, пределом справа) функции  в точке
в точке 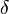 такое, что для всех точек
такое, что для всех точек  из интервала
из интервала  справедливо неравенство
справедливо неравенство  .
.
 справедливо неравенство
справедливо неравенство 
 (предел конечен и не равен 0), то
(предел конечен и не равен 0), то  и
и  являются бесконечно малыми величинами одного порядка малости. Это обозначается как
являются бесконечно малыми величинами одного порядка малости. Это обозначается как  или как одновременное выполнение отношений
или как одновременное выполнение отношений  и
и  . Следует заметить, что в некоторых источниках можно встретить обозначение, когда одинаковость порядков записывают в виде только одного отношения «о большое», что является вольным использованием данного символа.
. Следует заметить, что в некоторых источниках можно встретить обозначение, когда одинаковость порядков записывают в виде только одного отношения «о большое», что является вольным использованием данного символа. , то
, то  или
или  .
. , то бесконечно малые или бесконечно большие величины
, то бесконечно малые или бесконечно большие величины  ).
).

 ,
,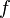
 , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.
, то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.