 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Інтервал і радіус збіжності степеневого ряду 12
ЛЕКЦІЯ 17-18. ФУНКЦІОНАЛЬНІ ТА СТЕПЕНЕВІ РЯДИ ПЛАН 1. Поняття функціонального ряду 2. Властивості рівномірно збіжних рядів 3. Степеневі ряди 4. Інтервал і радіус збіжності степеневого ряду 5. Диференціювання та інтегрування степеневих рядів 6. Зображення функцій степеневими рядами. Ряди Тейлора і Маклорена 7. Ряд Маклорена для деяких елементарних функцій 8. Застосування рядів для наближених обчислень 9. Ряд Фур’є Поняття функціонального ряду Означення 1. Ряд Якщо ряд (2) збігається (розбігається), то кажуть, що при х=х0збігається (розбігається) функціональний ряд (1). Означення 2. Усі значення аргументу х, при яких функціональний ряд збіжний, називаються областю збіжності функціонального ряду. В області збіжності існує границя часткових сум функціонального ряду
де функція Ряд В області збіжності функціонального ряду виконується формула Означення 3. Ряд (2) збіжний для всіх х із області Х, називається рівномірно збіжним у цій області, якщо для будь-якого числа
Ознака Вейєрштрасса.Якщо ряд, складений із абсолютних величин членів функціонального ряду, для всіх Приклад.Дослідити характер збіжності ряду Оскільки Властивості рівномірно збіжних рядів 1. Сума рівномірно збіжного ряду неперервних функцій є неперервна функція. 2. Якщо ряд (2) рівномірно збіжний на інтервалі (а; b) та існують границі
то виконується рівність
3. Якщо члени збіжного ряду (2) мають неперервні похідні для
4. Якщо члени ряду (2) неперервні, а сам ряд рівномірно збіжний для
У загальному випадку, при дослідженні на збіжність функціонального ряду використовується та сама методика, що і для знакозмінного ряду. Приклад. Знайти область збіжності ряду
Побудуємо ряд із абсолютних величин членів даного ряду
За ознакою Даламбера ряд буде збігатись, якщо
і розбігатись, якщо Залишається дослідити ряд на збіжність у точках х = 1 і х = 3. При х = 1 маємо ряд Степеневі ряди Означення 4. Функціональний ряд Розглядають і більш загальний вигляд степеневого ряду
Якщо в (4) візьмемо х – с = у, то дістанемо ряд типу (3), тому властивості ряду (3) неважко перефразувати і для ряду (4). Теорема (Абеля). Якщо степеневий ряд (3): 1) збігається при х = х0, то він абсолютно збігається для будь-якого х, що задовольняє нерівність 2) якщо ряд (3) розбігається при х = х1, то він розбігається при всіх х, що задовольняють нерівність Ілюстрацію до теореми Абеля наведено на рис. 1.
Рис. 1 Інтервал і радіус збіжності степеневого ряду Як наслідок із теореми Абеля для степеневого ряду (3) існує інтервал збіжності з центром у точці х = 0 (рис. 2).
Рис. 2 Означення 5.Інтервалом збіжності степеневого ряду називається такий інтервал, у всіх внутрішніх точках якого ряд збігається абсолютно, а для всіх точок Для узагальненого степеневого ряду (4) інтервал збіжності Зауваження. На кінцях інтервалу збіжності, тобто в точках х=–R, Виведемо формулу для знаходження радіуса збіжності ряду (3). Для цього побудуємо ряд із абсолютних величин членів ряду (3):
Нехай існує границя
При
Аналогічно, використовуючи радикальну ознаку Коші, можна дістати формулу для радіуса збіжності, степеневого ряду у вигляді: 5. Диференціювання та інтегрування степеневих рядів Степеневий ряд
Приклад. Знайти суму ряду Позначимо суму ряду через 12 |



 , (1). де членами ряду
, (1). де членами ряду  є функції від аргументу х, називається функціональним рядом. При х=х0 ряд (1) перетворюється на числовий
є функції від аргументу х, називається функціональним рядом. При х=х0 ряд (1) перетворюється на числовий  (2)
(2)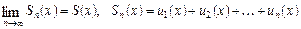 ,
, — сума ряду.
— сума ряду. називається залишком ряду.
називається залишком ряду. , де
, де 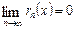 .
.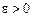 існує такий незалежний від х номер N, що при n > N виконується одночасно для всіх
існує такий незалежний від х номер N, що при n > N виконується одночасно для всіх  така нерівність:
така нерівність:
 мажорується одним і тим самим збіжним числовим рядом, то функціональний ряд буде рівномірно збіжним для
мажорується одним і тим самим збіжним числовим рядом, то функціональний ряд буде рівномірно збіжним для 
 .
. , тобто члени даного функціонального ряду для будь-якого х мажоруються членами збіжного числового ряду Діріхле
, тобто члени даного функціонального ряду для будь-якого х мажоруються членами збіжного числового ряду Діріхле  , то за ознакою Вейєрштрасса даний ряд буде рівномірно збіжним для
, то за ознакою Вейєрштрасса даний ряд буде рівномірно збіжним для  .
.

 та ряд складений із похідних членів ряду (2)
та ряд складений із похідних членів ряду (2)  рівномірно збіжний для
рівномірно збіжний для 
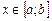 , то
, то

 . Цей ряд буде знакододатний. Отже, маємо право застосовувати до нього ознаку Даламбера, при цьому х вважатимемо деяким параметром:
. Цей ряд буде знакододатний. Отже, маємо право застосовувати до нього ознаку Даламбера, при цьому х вважатимемо деяким параметром:

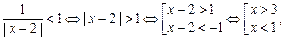
 .
. , а при х = 3 — ряд
, а при х = 3 — ряд  . Ці ряди розбігаються, бо, очевидно, для них не виконується необхідна умова збіжності. Таким чином, область збіжності функціонального ряду
. Ці ряди розбігаються, бо, очевидно, для них не виконується необхідна умова збіжності. Таким чином, область збіжності функціонального ряду  буде
буде  . У цій області ряд збігається абсолютно.
. У цій області ряд збігається абсолютно. (3) називається степеневим рядом, його загальний член
(3) називається степеневим рядом, його загальний член  ; числа
; числа  називаються коефіцієнтами степеневого ряду.
називаються коефіцієнтами степеневого ряду. (4)
(4) ;
; .
.

 ряд є розбіжним; при цьому число R>0 називається радіусом збіжності степеневого ряду.
ряд є розбіжним; при цьому число R>0 називається радіусом збіжності степеневого ряду. має центр симетрії в точці х = с.
має центр симетрії в точці х = с. ряд може як збігатись, так і розбігатись. Це питання потребує спеціального дослідження в кожному випадку.
ряд може як збігатись, так і розбігатись. Це питання потребує спеціального дослідження в кожному випадку. (5)
(5) . Тоді, застосовуючи ознаку Даламбера до ряду (5), дістаємо:
. Тоді, застосовуючи ознаку Даламбера до ряду (5), дістаємо: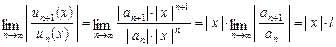 .
. ряд (5) збігається, а отже, ряд (3) збігається абсолютно; при
ряд (5) збігається, а отже, ряд (3) збігається абсолютно; при  ряд (5) розбігається. Розбіжність ряду, установлена за ознакою Даламбера, означає, що для цього ряду не виконується необхідна умова збіжності:
ряд (5) розбігається. Розбіжність ряду, установлена за ознакою Даламбера, означає, що для цього ряду не виконується необхідна умова збіжності:  , а тому не виконується необхідна умова збіжності і для ряду (3)
, а тому не виконується необхідна умова збіжності і для ряду (3)  , і ряд (3) при
, і ряд (3) при  . Радіус збіжності визначається за формулою
. Радіус збіжності визначається за формулою . (6)
. (6) .
.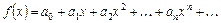 буде рівномірно збіжним на будь-якому відрізку із його інтервалу збіжності
буде рівномірно збіжним на будь-якому відрізку із його інтервалу збіжності  , а тому на такому відрізку його можна почленно диференціювати та інтегрувати, при цьому мають місце рівності:
, а тому на такому відрізку його можна почленно диференціювати та інтегрувати, при цьому мають місце рівності:

 і знайдемо похідну
і знайдемо похідну  :
:  . Одержали ряд геометричної прогресії зі знаменником q = x і першим членом u1 = 1. Цей ряд буде збіжним при
. Одержали ряд геометричної прогресії зі знаменником q = x і першим членом u1 = 1. Цей ряд буде збіжним при  , а його сума має вигляд:
, а його сума має вигляд:  . Розв’язуючи це диференціальне рівняння, дістаємо
. Розв’язуючи це диференціальне рівняння, дістаємо  . Зауважимо, що формула
. Зауважимо, що формула  справджується на інтервалі збіжності
справджується на інтервалі збіжності 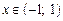 .
.