 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Дії з комплексними числами, поданими в тригонометричній формі 12
Додавати і віднімати комплексні числа простіше і зручніше, коли компоненти подані в алгебраїчній формі. Зовсім інша річ з останніми чотирма алгебраїчними діями. Множення. Нехай треба перемножити числа:
Дістанемо:
Звідси випливає: Модуль добутку двох комплексних чисел дорівнює добуткові модулів співмножників, а аргумент — сумі аргументів співмножників. Приклад. Нехай:
Тоді Ділення. Нехай треба число a = R1(cos a + sin a) поділити на число b = R2 (cos b +i sin b). Матимемо:
Модуль частки двох комплексних чисел дорівнює частці модулів, а аргумент — різниці аргументів діленого і дільника. Приклад. Нехай a=12 (cos55°+i sin55°); b=3(cos35°+i sin 35°). Тоді Піднесення до степеня. Нехай треба число a = R(cos a + i sin a) піднести до степеня n: Матимемо:
Модуль степеня комплексного числа дорівнює тому самому степеню модуля основи, а аргумент — аргументові основи, помноженому на показник степеня. У частинному випадку, якщо r = 1, формула (7) набуває вигляду
Ця формула має назву формули Муавра. Приклад. Піднести до куба число a = 2 (cos 20° + i sin 20°). Матимемо:
Формула Ейлера:
Добування кореня. Добудемо корінь n-го степеня з числа:
Матимемо:
1. Модуль кореня n-го степеня з комплексного числа дорівнює кореню того самого степеня з модуля підкореневого числа, а аргумент — аргументові підкореневого числа, поділеному на показник кореня. 2. Корінь n-го степеня з комплексного числа має n різних значень. За допомогою формули Ейлера можна дістати показникову форму комплексного числа 6. Квадратний тричлен з комплексними числами Дано тричлен y = ax2 + bx + c. Відомо, що корені його комплексні. У цьому випадку
Додамо й віднімемо по
При всіх значеннях х вираз Дослідимо, який знак має другий доданок У випадках комплексних коренів вираз b2 – 4ac від’ємний, а протилежне йому число – (b2 – 4ac), тобто 4ac – b2, — число додатне. Знаменник 4а2 теж число додатне, а отже, дріб Звідси випливає, що знак числової величини тричлена залежить лише від знака а: при а додатному тричлен має додатні значення, при а від’ємному - від’ємні. Якщо тричлен має комплексний корінь, то при всіх значеннях х його числове значення має той самий знак, що й коефіцієнт при х2. Загальний висновок про квадратні рівняння Загальна формула для коренів повного квадратного рівняння виду ax2 + bx + c = 0 буде
Корені квадратного рівняння будуть обидва дійсні або обидва уявні залежно від того, чи буде дискримінант (у перекладі розрізнювач) b2 – 4ac величиною додатною чи від’ємною: 1. b2 – 4ac > 0. У цьому випадку вираз під коренем додатний. Квадратний корінь з цього виразу має два значення, і, отже, рівняння має два різні дійсні корені:
2. b2 – 4ac = 0. У цьому випадку другий член чисельника дорівнює нулю і рівняння має два рівні корені: 3. b2 – 4ac < 0. У цьому випадку рівняння має два комплексно спряжені корені:
12 |



 ,
,  .
. (5)
(5) ;
;  .
. .
.
 . (6)
. (6) .
. . (7)
. (7) .
.
 .
. ,
,  ,
, ,
,  .
. .
. (8)
(8)
 . Перетворимо тричлен до вигляду
. Перетворимо тричлен до вигляду .
. :
: ;
;  .
. є число додатне або таке, що дорівнює нулю (при
є число додатне або таке, що дорівнює нулю (при  ).
). .
.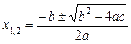 .
. ;
;  .
. .
. ,
,  .
.