 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Тригонометрична форма комплексного числа 12
ЛЕКЦІЯ 11. Комплексні числа ПЛАН 1. Поняття комплексних чисел 2. Дії з комплексними числами 3. Геометричне зображення комплексного числа (інтерпретація Гаусса) 4. Тригонометрична форма комплексного числа 5. Дії з комплексними числами, поданими в тригонометричній формі 6. Квадратний тричлен з комплексними числами 7. Загальний висновок про квадратні рівняння Поняття комплексних чисел Означення 1. Комплексним числом називається число виду Означення 2. Комплексні числа виду a + bi і a – bi називаються спряженими. Комплексні числа виду a + bi і – a – bi називаються протилежними. Спряжене до комплексного числа z позначається Означення 3. Два комплексних числа a + bi і a1 + b1i вважаються рівними в тому і тільки в тому випадку, якщо a = a1 і b = b1. Зауваження. Щодо комплексних чисел не прийнято жодної угоди, яке з них вважати більшим. Дії з комплексними числами Додавання: (a + bi) + (a1 + b1і) = (a + a1) + (b + b1)i. Віднімання: (a + bi) – (a1 + b1i) = (a – a1) + (b – b1)i. Множення: (a + bi)(a1 + b1i) = aa1 + a1bi + ab1i + bb1i2 = (aa1 – Ділення:
Піднесення до степеня: спочатку знайдемо результати від піднесення до степеня уявної одиниці, знаючи, що за умовою і2 треба вважати таким, що дорівнює – 1. і0 = 1 і5 = і4 × і = і і1 = і і6 = і5 × і = – 1 і2 = – 1 і7 = і6 × і = – 1 × і = – і і3 = і2 × і = – і і8 = і7 × і = – і × і = 1 і4 = і3 × і = – і × і = 1 і т. п. Отже, дістали чотири значення, що чергуються: і; – 1; – і; + 1, тоді: (а + ib)2 = a2 + 2abi + b2i2 = (a2 – b2) + 2abi, (а + ib)3 = a3 + 3a2b + 3a(ib)2 + (ib)3 = (a3 – 3ab2) + (3a2b – b3)i і т. п. Добування квадратного кореня: Припустимо, що Тоді a + bi = (x2 – y2) + 2xyi. Отже, маємо:
З рівняння 2ху = b випливає, що знаки х та у мають бути однакові, якщо b > 0, і різні, якщо b < 0. Тому
Зауваження. Для того щоб з комплексного числа можна було добути корінь третього, або вищого степеня, йому треба надати іншого вигляду. Приклад. Нехай z1 = 5 + i6; z2 = 7 – i9; z3 = 5 + 12i. Знайти: z1 + z2, z1 × z2, z1 / z2, z12, z1 + z2 = (5 + 6і) + (7 – 9і) = (5 + 7) + і(6 – 9) = 12 – 3і; z1 × z2 = (5 + 6і) × (7 – 9і) = 5 × 7 + 6і × 7 – 5 × 9і – і6 × і9 =
z12 = (5 + i6)2 = 25 + 2 × 5 × 6i + (i6)2 = 25 + 60i – 36 = – 11 + 60i;
3. Геометричне зображення комплексного числа (інтерпретація Гаусса) Будь-яке комплексне число a + bi можна зобразити геометрично. Візьмемо в площині прямокутну систему координат і, вибравши одиницю довжини, зображатимемо дійсні числа на осі абсцис, а уявні — на осі ординат. Відповідно до цього вісь абсцис називається дійсною віссю, а вісь ординат - уявною. Число a + bi зображатимемо точкою площини, абсциса якої чисельно дорівнює а, а ордината дорівнює b (рис. 1).
Тригонометрична форма комплексного числа Зображення комплексних чисел за допомогою точок на площині дає змогу подати число a + bi в іншому вигляді, а саме — у тригонометричній формі. Нехай точка М (рис. 2) зображає комплексне число a + ib. Тоді ОА = а, АМ = b. Позначимо віддаль ОМ точки від початку координат через r, а кут АОМ, утворюваний ОМ з віссю х, — через j. Тоді з трикутника АОМ матимемо: a = r cosj, b = r sinj. (1) Підставивши в комплексне число a + bi значення a і b (1), дістанемо a + bi = r cos j + r sin j × i або a + bi = r (cos j + i sin j). (2) Це є тригонометрична форма комплексного числа. Довжина OM = r називається модулем комплексного числа, а кут АОМ = j — його аргументом. Покажемо, як перетворити в тригонометричну форму комплексне число, подане в звичайній алгебраїчній формі. Для цього треба знайти r і j за даними a і b. З трикутника ОАМ (рис. 2) маємо:
Приклад. Подати в тригонометричній формі число – 3 + 2і. З формул (3) маємо:
Тангенс від’ємний, отже, кут j треба шукати в ІІ або IV чверті. З формул (4) виходить, що при а = – 3 і b = 2 синус буде додатний, а косинус — від’ємний, тобто j буде кутом ІІ чверті. На ПОМ або за таблицями знаходимо: j = 146° 18¢, а тому 12 |



 , де a, b — дійсні числа, і2 = – 1. Число а називається дійсною частиною, bi — уявною частиною, і — уявною одиницею. Множина комплексних чисел позначається С.
, де a, b — дійсні числа, і2 = – 1. Число а називається дійсною частиною, bi — уявною частиною, і — уявною одиницею. Множина комплексних чисел позначається С. .
.
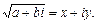

 .
. при b > 0;
при b > 0; при b < 0.
при b < 0. .
.

 .
.
 ,
,  , (3)
, (3) ,
,  (4)
(4)
 ,
, 

 .
.