 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Некоторые приложения частных производных.
Уравнение касательной плоскости к поверхности  в точке в точке  имеет вид имеет вид  , ,
а уравнение нормали – вид 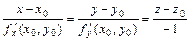 . . В случае задания поверхности неявным уравнением  : :  - уравнение касательной плоскости к поверхности в точке - уравнение касательной плоскости к поверхности в точке  и и  - уравнение нормали. - уравнение нормали.
6.72 Написать уравнения касательной плоскости и нормали в точке  к следующим поверхностям: к следующим поверхностям: а)  ; б) ; б)  ; ; в)  ; ; г)  6.73 Написать уравнения касательной плоскости и нормали в точке  к следующим поверхностям: к следующим поверхностям: а)  ; ; б)  ; в) ; в)  ; ; г)  . . 6.74 Для поверхности  найти уравнение касательной плоскости, параллельной плоскости найти уравнение касательной плоскости, параллельной плоскости  6.75 Для поверхности  найти уравнение нормали, параллельной прямой найти уравнение нормали, параллельной прямой  Множество точек  называется выпуклым, если вместе с любыми двумя своими точками называется выпуклым, если вместе с любыми двумя своими точками  и и  , оно содержит и отрезок , оно содержит и отрезок  . . Функция  , определённая на выпуклом множестве , определённая на выпуклом множестве  называется выпуклой вверх, если для всех точек называется выпуклой вверх, если для всех точек  , где , где  , ,  и для любого и для любого  выполняется неравенство выполняется неравенство  и выпуклой вниз, если и выпуклой вниз, если  . . Матрица  называется матрицей Гессе функции называется матрицей Гессе функции  в точке в точке  . . Дважды дифференцируемая на выпуклом множестве  функция функция  является на этом множестве: 1) выпуклой вниз, если является на этом множестве: 1) выпуклой вниз, если  при всех при всех 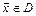 ; 2) выпуклой вверх, если ; 2) выпуклой вверх, если  при всех при всех 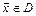 . Если на множестве . Если на множестве  матрица Гессе матрица Гессе  функции функции  знакопеременна, то знакопеременна, то  на этом множестве выпуклой не является. на этом множестве выпуклой не является. Знакоопределённость матрицы Гессе устанавливают, используя критерий Сильвестра знакоопределённости матриц квадратичных форм. 6.76.Исследовать следующие функции на выпуклость: а)  ; б) ; б)  ; ; в)  ; г) ; г)  . . Частные эластичности функции  вычисляются по формулам: вычисляются по формулам:  , , 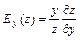 . Частные эластичности . Частные эластичности  , ,  являются мерами реагирования переменной являются мерами реагирования переменной  на изменение переменных на изменение переменных  и и  , и показывают приближённый процентный прирост , и показывают приближённый процентный прирост  при изменении при изменении  и и  на один процент, соответственно. на один процент, соответственно. Под производственной функцией понимается функция  , независимые переменные которой , независимые переменные которой  имеют смысл объёмов используемых ресурсов, а зависимая переменная имеют смысл объёмов используемых ресурсов, а зависимая переменная  – объёма выпускаемой продукции. – объёма выпускаемой продукции. Предельной по переменной 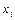 для для  называется величина называется величина  , средней– величина , средней– величина  . Буква . Буква  - сокращение от слова - сокращение от слова  (предельный), буква (предельный), буква  - сокращение от слова - сокращение от слова  (средний). (средний). Производственной функцией Кобба-Дугласа называется функция вида  , где , где 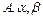 - некоторые постоянные, - некоторые постоянные,  - объём производственных фондов, - объём производственных фондов,  - объём трудовых ресурсов, - объём трудовых ресурсов,  - объём выпускаемой продукции. - объём выпускаемой продукции. 6.77.Найти частные эластичности  и и  функций функций  в указанных точках в указанных точках 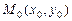 : : а)  , ,  ; б) ; б)  , ,  . . 6.78Для заданных значений  и и 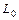 найти: а) среднюю и предельную производительности труда; б) среднюю и предельную фондоотдачу; в) эластичности выпуска по труду и по фондам, если производственная функция Кобба-Дугласа имеет вид: найти: а) среднюю и предельную производительности труда; б) среднюю и предельную фондоотдачу; в) эластичности выпуска по труду и по фондам, если производственная функция Кобба-Дугласа имеет вид: 1)  , ,  , ,  ; ; 2)  , ,  , ,  . . Формула Тейлора. Если функция  дифференцируема дифференцируема  раз в точке раз в точке  , то при , то при  имеет место формула Тейлора (порядка имеет место формула Тейлора (порядка  ) с остаточным членом в форме Пеано ) с остаточным членом в форме Пеано  , ,
где  при при  . Частный случай формулы Тейлора в точке . Частный случай формулы Тейлора в точке  называется формулой Маклорена. называется формулой Маклорена. 6.79 Разложить по формуле Тейлора следующие функции в окрестности указанных точек: а)  ; ; б)  ; ; в)  ; ; г)  ; ; д)  ; ; е)  . . 6.80 Выписать члены до второго порядка включительно формулы Тейлора для функции  в окрестности точки в окрестности точки 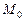 : : а)  ; б) ; б)  ; ; в)  . . 6.81 Разложить функции  по формуле Маклорена до членов третьего порядка включительно: по формуле Маклорена до членов третьего порядка включительно: а)  ; б) ; б)  . .
|




 в точке
в точке  имеет вид
имеет вид ,
,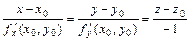 .
. :
:  - уравнение касательной плоскости к поверхности в точке
- уравнение касательной плоскости к поверхности в точке  и
и - уравнение нормали.
- уравнение нормали. к следующим поверхностям:
к следующим поверхностям: ; б)
; б)  ;
; ;
;
 ;
; ; в)
; в)  ;
; .
. найти уравнение касательной плоскости, параллельной плоскости
найти уравнение касательной плоскости, параллельной плоскости 
 найти уравнение нормали, параллельной прямой
найти уравнение нормали, параллельной прямой 
 называется выпуклым, если вместе с любыми двумя своими точками
называется выпуклым, если вместе с любыми двумя своими точками  и
и  , оно содержит и отрезок
, оно содержит и отрезок  .
. , определённая на выпуклом множестве
, определённая на выпуклом множестве  называется выпуклой вверх, если для всех точек
называется выпуклой вверх, если для всех точек  , где
, где  ,
,  и для любого
и для любого  выполняется неравенство
выполняется неравенство  и выпуклой вниз, если
и выпуклой вниз, если  .
. называется матрицей Гессе функции
называется матрицей Гессе функции  .
. функция
функция  является на этом множестве: 1) выпуклой вниз, если
является на этом множестве: 1) выпуклой вниз, если  при всех
при всех 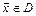 ; 2) выпуклой вверх, если
; 2) выпуклой вверх, если  при всех
при всех  функции
функции  на этом множестве выпуклой не является.
на этом множестве выпуклой не является. ; б)
; б)  ;
; ; г)
; г)  .
. ,
, 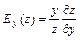 . Частные эластичности
. Частные эластичности  ,
,  являются мерами реагирования переменной
являются мерами реагирования переменной  на изменение переменных
на изменение переменных  и
и  , и показывают приближённый процентный прирост
, и показывают приближённый процентный прирост  имеют смысл объёмов используемых ресурсов, а зависимая переменная
имеют смысл объёмов используемых ресурсов, а зависимая переменная 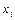 для
для  , средней– величина
, средней– величина  . Буква
. Буква  - сокращение от слова
- сокращение от слова  (предельный), буква
(предельный), буква  (средний).
(средний). , где
, где 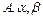 - некоторые постоянные,
- некоторые постоянные,  - объём производственных фондов,
- объём производственных фондов,  - объём трудовых ресурсов,
- объём трудовых ресурсов,  - объём выпускаемой продукции.
- объём выпускаемой продукции. и
и  функций
функций  в указанных точках
в указанных точках 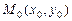 :
: ,
,  ; б)
; б)  ,
,  .
. и
и 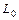 найти: а) среднюю и предельную производительности труда; б) среднюю и предельную фондоотдачу; в) эластичности выпуска по труду и по фондам, если производственная функция Кобба-Дугласа имеет вид:
найти: а) среднюю и предельную производительности труда; б) среднюю и предельную фондоотдачу; в) эластичности выпуска по труду и по фондам, если производственная функция Кобба-Дугласа имеет вид: ,
,  ,
,  ;
; ,
,  ,
,  .
. дифференцируема
дифференцируема  раз в точке
раз в точке  , то при
, то при  имеет место формула Тейлора (порядка
имеет место формула Тейлора (порядка  ,
, при
при  называется формулой Маклорена.
называется формулой Маклорена. ;
; ;
; ;
; ;
; ;
; .
. в окрестности точки
в окрестности точки 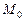 :
: ; б)
; б)  ;
; .
. ; б)
; б)  .
.