 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Дифференцирование сложных и неявных функций.
Частные производные Частной производной (1-ого порядка) функции Частные производные вычисляются по обычным правилам дифференцирования функции одной переменной, в предположении, что все аргументы функции, кроме аргумента Частными производными второго порядка функции
Производные
Если смешанные частные производные, подлежащие вычислению, непрерывны, то результат многократного дифференцирования функции по различным переменным не зависит от порядка дифференцирования. В задачах 6.22-6.32 найти частные производные 6.22 6.24 В задачах 6.33-6.34 найти частные производные 6.33 6.35Проверить равенство а) 6.36Проверить равенство В задачах 6.37-6.40 найти указанные частные производные: 6.37 Дифференциал. Полным приращением функции Функция Полным дифференциалом Функция Форма записи первого дифференциала не изменится и в том случае, если переменные Дифференциалом 2-ого порядка функции Если а для функции
Для функции Если функция В задачах 6.41-6.46 найти дифференциалы первого и второго порядков от следующих функций: 6.41 6.44 6.47Найти значение полного дифференциала функции 6.48Найти значение полного дифференциала функции Первый дифференциал применяют для приближённого вычисления значений функции В частности, для функции 6.49Вычислить приближенно: а) ж) 6.50На сколько приближённо изменятся диагональ и площадь прямоугольника со сторонами 6.51Центральный угол сектора 6.52Прямоугольный параллелепипед имеет измерения: 6.53Цилиндрический стакан имеет внутренние размеры: радиус основания R=2.5 м, высоту Н=4м и толщину стенок l=1дм. Найти приближенно объем материала, затраченного на изготовление стакана. 6.54 В усеченном конусе радиусы оснований R=20 см, r=10 см и высота h=30 см. Как приближенно изменится объем конуса 6.55 Найти в указанной точке второй дифференциал функций: а) Дифференцирование сложных и неявных функций. |



 в точке
в точке 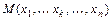 по переменной
по переменной  называется предел
называется предел  , если этот предел существует. Частную производную обозначают
, если этот предел существует. Частную производную обозначают  или
или  .
. ,
,  (
(  ).
). (
(  частные производные обозначаются:
частные производные обозначаются: ,
,  ,
,  ,
,  ,
,  ,
,  ,… или
,… или  ,….
,…. от следующих функций:
от следующих функций: . 6.23
. 6.23  .
. . 6.25
. 6.25  . 6.26
. 6.26  . 6.27
. 6.27  . 6.28
. 6.28  . 6.29
. 6.29  . 6.30
. 6.30  . 6.31
. 6.31  . 6.32
. 6.32  .
. от следующих функций:
от следующих функций: . 6.34
. 6.34  .
. , если
, если ; б)
; б)  .
. , если
, если  , если
, если  . 6.38
. 6.38  , если
, если  . 6.39
. 6.39  ,если
,если  .6.40
.6.40  ,если
,если  .
. в точке
в точке  , соответствующим приращениям аргументов
, соответствующим приращениям аргументов  называется разность
называется разность  .
. , где
, где 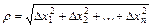
 при
при  ,
, 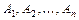 - числа, не зависящие от
- числа, не зависящие от  функции
функции  называется главная, линейная относительно
называется главная, линейная относительно  полного приращения
полного приращения  функции, равная
функции, равная  , где
, где  .
. являются функциями новых, независимых переменных (свойство инвариантности формы первого дифференциала).
являются функциями новых, независимых переменных (свойство инвариантности формы первого дифференциала).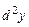 , т. е.
, т. е.  . В общем дифференциалом порядка
. В общем дифференциалом порядка  называется дифференциал от дифференциала
называется дифференциал от дифференциала  -ого порядка и обозначается
-ого порядка и обозначается  , т.е.
, т.е.  .
. - независимая переменная, то для нахождения дифференциала
- независимая переменная, то для нахождения дифференциала  , формально раскрываемая по биномиальному закону. Например, для функции
, формально раскрываемая по биномиальному закону. Например, для функции  ,
,  ,
, - формулы:
- формулы:  ,
, .
.
 , то в этой точке значение любой смешанной частной производной
, то в этой точке значение любой смешанной частной производной  . 6.42
. 6.42  . 6.43
. 6.43  .
. . 6.45
. 6.45  . 6.46
. 6.46 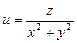 .
. при
при 
 при
при 
 в малой окрестности точки
в малой окрестности точки  , в которой функция дифференцируема, по формуле:
, в которой функция дифференцируема, по формуле:  .
. , где
, где  ,
,  . Чем меньше значение
. Чем меньше значение  , тем точнее формула.
, тем точнее формула. ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ;
; ; з)
; з)  .
. ,
,  , если первая сторона увеличится на
, если первая сторона увеличится на  , а вторая уменьшится на
, а вторая уменьшится на  ?
? увеличился на
увеличился на  . На сколько следует приближённо уменьшить радиус сектора
. На сколько следует приближённо уменьшить радиус сектора  , чтобы площадь сектора осталась без изменения?
, чтобы площадь сектора осталась без изменения? ,
,  ,
,  . На сколько приближённо изменится длина его диагонали, если
. На сколько приближённо изменится длина его диагонали, если  увеличится на
увеличится на  ,
,  увеличится на
увеличится на  ,
,  уменьшится на
уменьшится на  .
.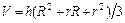 , если R увеличить на 2мм, r увеличить на 3мм, а h уменьшить на 1 мм?
, если R увеличить на 2мм, r увеличить на 3мм, а h уменьшить на 1 мм? ; б)
; б)  .
.