 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задание по математической статистике 12
1 Постройте статистическую модель случайного вектора (x ,h) в виде
2.Найдите эмпирические законы распределения 3. Найдите выборочным методом: · · · в предположении, что истинные законы распределения неизвестны, а функция регрессии линейна. Являются ли найденные оценки состоятельными? Исследуйте 4.Найдите оценки 5.Постройте центральный доверительный интервал надежности 0.95 для параметра k. Накрывает ли он истинное k=3? Можно ли перейти от построенного доверительного интервала к доверительному интервалу для 6.Постройте двойственный критерий для проверки гипотез относительно значений k. Каков вид гипотез? Найдите a. Возьмите 7.Постройте критерий для проверки гипотез
Вариант 11 Рассматривается случайный вектор (
функции регрессии и ее оптимального линейного приближения. Задание по математической статистике 1. Постройте статистическую модель случайного вектора (x ,h) и 2.Найдите эмпирические законы распределения 3. Найдите выборочным методом: · · · в предположении, что истинные законы распределения неизвестны, а функция регрессии линейна. Являются ли найденные оценки состоятельными? Исследуйте 4.Найдите оценки Найдите оценку 5.Для параметра 6.Постройте критерий для проверки гипотез
Вариант 12 Рассматривается случайный вектор (
12 |



 ,
, 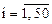 .
.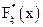 и
и  . Проверьте гипотезу о согласованности
. Проверьте гипотезу о согласованности  по критериям Колмогорова и Пирсона, приняв в качестве гипотетического закона распределения x ее истинный закон распределения. Нарисуйте графики
по критериям Колмогорова и Пирсона, приняв в качестве гипотетического закона распределения x ее истинный закон распределения. Нарисуйте графики  на другом.
на другом. для x и h,
для x и h, ,
, 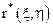 ,
,
 на несмещенность и асимптотическую несмещенность. Являются ли
на несмещенность и асимптотическую несмещенность. Являются ли  и
и  для параметра k закона распределения x и сравните их с теоретическим значением параметра. Выясните свойства оценок.
для параметра k закона распределения x и сравните их с теоретическим значением параметра. Выясните свойства оценок. ?
? =3. Проверьте гипотезы.
=3. Проверьте гипотезы.

 . Возьмите
. Возьмите 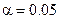 . Найдите функцию мощности и постройте ее график.
. Найдите функцию мощности и постройте ее график. ), причем
), причем
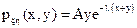 , x > 0, y > 0, параметр
, x > 0, y > 0, параметр  > 0.
> 0.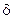 в виде
в виде  ,
,  .
. и
и  . Проверьте гипотезу о согласованности
. Проверьте гипотезу о согласованности 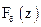 по критериям Колмогорова и Пирсона, приняв в качестве гипотетического закона распределения
по критериям Колмогорова и Пирсона, приняв в качестве гипотетического закона распределения  на другом.
на другом. для
для  ,
,  ,
,
 и
и  для параметра
для параметра  и сравните их с теоретическим значением параметра. Выясните свойства оценок.
и сравните их с теоретическим значением параметра. Выясните свойства оценок. .
. . Можно ли перейти от построенного доверительного интервала к доверительному интервалу для
. Можно ли перейти от построенного доверительного интервала к доверительному интервалу для  ? Накрывают ли эти интервалы истинные характеристики?
? Накрывают ли эти интервалы истинные характеристики?
 . Возьмите
. Возьмите  ,
,  , 0 < x < 1, 1 < y <
, 0 < x < 1, 1 < y <  , параметр c > 0.
, параметр c > 0.