 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Средние характеристики ряда динамики
Для обобщающей характеристики динамики используют два типа средних показателей: - средние уровни ряда; - средние показатели изменения уровней ряда. Порядок расчета среднего уровня различается для отдельных видов рядов динамики. Для рядов динамики с равноотстоящими во времени уровнями порядок расчета среднего уровня следующий: а) находим средний уровень интервального ряда абсолютных величин:
б) определяем средний уровень моментного ряда абсолютных величин:
Для моментного ряда с неравными промежутками времени при известных точных датах изменения уровней ряда средний уровень определяется по формуле
где t – время, в течение которого сохранялся уровень.
Например, количество обслуживаемых филиалом банка счетов клиентов с 1 по 15 января составляло 300 счетов (t1 = 15 дней); с 16 января по 20 марта – 370 счетов (t2 = 65 дней), с 21 марта по 1 апреля – 390 счетов (t3 = 10 дней). Среднее количество обслуживаемых счетов клиентов за квартал
Средние показатели изменения уровней ряда включают: - средний абсолютный прирост ( - средний коэффициент роста ( - средний темп роста ( - средний темп прироста ( Средний абсолютный прирост показывает, на сколько единиц в среднем увеличивался или уменьшался каждый уровень ряда по сравнению с предыдущим за ту или иную единицу времени (в среднем ежемесячно, ежегодно и т.п.). Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня ряда. Его рассчитывают в зависимости от исходных данных следующими способами: 1) как простую среднюю арифметическую из абсолютных приростов (цепных) за последовательные промежутки времени
где t – продолжительность периода.
2) как частное от деления базисного абсолютного прироста конечного уровня ряда на продолжительность периода (число усредняемых отрезков времени от базисного до сравниваемого периода):
3) через накопленный (базисный абсолютный прирост (
Средний коэффициент роста (снижения) показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. Для его вычисления используют формулу геометрической средней в предположении, что соблюдается равенство фактического отношения конечного уровня к начальному при замене фактических темпов на средние. В зависимости от наличия исходных данных расчет проводят следующим образом: 1) если исходной информацией служат цепные коэффициенты роста, то формула имеет вид:
где П – произведение цепных показателей динамики.
2) через базисный коэффициент роста конечного периода (
3) если известны уровни динамического ряда
Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах (
Пример 7.1. По данным статистического наблюдения получены следующие данные о динамике занятого населения и области, тыс. человек:
По данным ряда динамики определите: 1. Среднегодовую численность занятого населения. 2. Абсолютные приросты - цепные и базисные. 3. Темпы роста и прироста - цепные и базисные. 4. Среднегодовой темп роста и прироста. Постройте график динамики занятого населения. Дайте анализ исчисленных показателей и сделайте выводы. Результаты расчетов по п. 2 и 3 представьте в табличном виде.
Решение:
Таблица. Расчет показателей ряда динамики
Абсолютный прирост:
базисный
цепной
Темп роста
базисный
цепной
Темп прироста:
базисный
цепной
Абсолютное значение 1 % прироста:
Среднегодовая численность занятого населения исчисляется по формуле средней арифметической простой:
Среднемесячный темп роста:
Среднемесячный темп прироста:
Рисунок 7.1. Динамика численности занятых
За обследованный период численность занятых снижалась, о чем свидетельствуют отрицательные абсолютные приросты и темпы прироста, а также величина темпа роста меньше единицы. Средняя численность занятых за полугодие составила 563,4 тыс. человек, ежегодное снижение численности занятых в среднем составило составил 2,6 %.
|



 ;
; .
. ,
,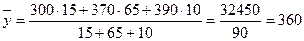 счетов.
счетов. );
); );
); );
); ).
). ,
, ;
; ):
): .
. ,
, )
) .
. .
. ). Отсюда средний темп прироста
). Отсюда средний темп прироста .
. ;
; .
. ;
; .
.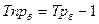 ;
; .
.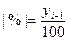 .
. ;
; руб.
руб. ;
; .
. .
. (- 2,6 %).
(- 2,6 %).