 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Показатели динамики уровней ряда
АНАЛИЗ РЯДОВ ДИНАМИКИ Понятие о рядах динамики Ряд динамики (динамический ряд, временной ряд) представляет собой ряд расположенных в хронологической последовательности статистических величин, которые отражают развитие изучаемых явлений. Каждый ряд динамики имеет два основных элемента: - время (t); - уровень ряда (yi), т.е. конкретные значения показателя. Уровни динамического ряда могут быть выражены абсолютными, средними и относительными величинами. Примером такого представления уровней ряда динамики являются данные об изменении отдельных социально-экономических показателей по Российской Федерации (табл. 7.1).
Таблица 7.1. Социально-экономические показатели по Российской Федерации за 2003 – 2007 гг.
Данные, приведенные в таблице 7.1, могут быть использованы для иллюстрации рядов динамики разного типа. Различают следующие виды рядов динамики: - моментные и интервальные; - ряды с равно- и неравноотстоящими во времени уровнями; - стационарные и нестационарные. Моментным является ряд динамики, уровни которого характеризуют изучаемое явление в конкретный момент времени. Такие ряды используют для описания величин типа запаса (остатки средств на счетах клиентов, объем собственных средств (капитала), объем основных фондов и т.д. Интервальным является ряд динамики, уровни которого характеризуют накопленный результат изменения явлений за определенные промежутки (интервалы, периоды) времени. Таким образом, интервальные ряды динамики используют для описания величин типа экономического потока, операции (проценты полученные, проценты уплаченные, комиссионные доходы и расходы, выпуск продукции, текущие затраты и т.п.). Уровни интервальных рядов динамики обладают свойством суммарности, показатели моментных рядов такого свойства не имеют. Можно сложить показатели объема промышленной продукции за кварталы и получить итог производства за год. Но если за год сложить данные о числе рабочих на начало каждого квартала, полученная сумма не будет иметь реального смысла. В рядах с равноотстоящими уровнями даты регистрации или окончания периодов представлены через равные, следующие друг за другом отрезки времени. В рядах с неравноотстоящими уровнями принцип равенства отрезков времени не соблюдается. Ряд динамики, в изменении уровней которого не наблюдается общей направленности (тенденции), является стационарным. Напротив, нестационарный ряд отличается наличием общей направленности в изменении уровней изучаемого показателя. При построении и анализе динамических рядов необходимо учитывать требование сопоставимости данных как в рамках одного ряда, так и в разных динамических рядах, если их исследуют совместно. Сопоставимость уровней динамического ряда рассматривают в нескольких аспектах: - по кругу охватываемых объектов; - по территории; - по методологии расчета показателей.
Показатели динамики уровней ряда При изучении динамики явлений для характеристики особенности их развития на отдельных этапах рассчитывают производные показатели: абсолютный прирост, коэффициент роста, темп роста и прироста, абсолютное значение 1 % прироста. Расчет основан на сравнении уровней ряда динамики. В зависимости от базы сравнения различают базисные и цепные показатели динамики. Базисные показатели динамики – это результат сравнения текущих уровней с одним фиксированным уровнем, принятым за базу. Они характеризуют окончательный результат всех изменений в уровнях ряда за период от базисного до текущего уровня. Обычно за базу сравнения принимают начальный уровень динамического ряда. Цепные показатели динамики – это результат сравнения текущих уровней с непосредственно предшествующим. Они характеризуют интенсивность изменения уровней от срока к сроку. Абсолютный прирост равен разности между текущим уровнем и уровнем более раннего периода. Интерпретацию абсолютного прироста осуществляют в тех же единицах измерения, в которых измеряют уровни ряда, с добавлением единицы времени, за которую определено изменение. Например, абсолютный прирост объема промышленной продукции составил 501 млрд. руб. за квартал и 687 трлн. руб. за год. Если текущий уровень уменьшился по сравнению с предыдущим периодом, то абсолютный прирост, имея отрицательное значение, характеризует абсолютную убыль (сокращение) уровня. Абсолютный прирост за единицу времени отражает абсолютную скорость изменения. Формулы абсолютного изменения уровня динамического ряда следующие: - цепного - базисного где
Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных приростов равна соответствующему базисному приросту за весь период. Для оценки эффективности изменения уровня динамического ряда используют относительные показатели динамики: - коэффициент роста, выраженный в долях единицы; - темп роста, выраженный в процентах. Коэффициент роста Кр определяют по формулам: - цепной - базисный Взаимосвязь цепных и базисных коэффициентов роста заключается в следующем: а) произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период; б) частное от деления последующего базисного коэффициента роста на предыдущий равна соответствующему цепному коэффициенту роста. Для большей простоты и наглядности доказательства этой взаимосвязи используем данные за три периода: а) б) Коэффициент роста показывает, во сколько раз увеличился уровень динамического ряда по сравнению с базисным, а в случае уменьшения – какую часть базисного составляет сравниваемый уровень. Темпы и коэффициенты роста отличаются только единицами измерения. Формулы расчета темпов роста следующие: - цепного - базисного Темпы прироста (сокращения) так же, как и темпы роста, исчисляют по годам (цепным методом) и накопленным итогом за длительный период (базисным методом). Формулы расчета темпов прироста следующие: - цепного
- базисного
Темп прироста показывает, на сколько процентов изменилась величина уровня динамического ряда за изучаемый период времени. Если она сокращается, то темпы прироста будут иметь знак «минус» и характеризовать относительное уменьшение уровней ряда. Для правильной интерпретации относительных показателей динамики явлений рекомендуется рассматривать их совместно с исходными уровнями ряда. Если уровень ряда принимает положительные и отрицательные значения (например, финансовый результат деятельности организации может быть прибылью или убытком), то темпы изменения и прироста не имеют экономической интерпретации и не рассчитываются. Для цепных показателей прироста и его темпов рассчитывают показатель абсолютного значения одного процента прироста. Он равен отношению абсолютного прироста (цепного) к темпу прироста (цепному). Этот показатель может быть исчислен и иначе, т.е. как одна сотая часть предыдущего уровня:
Аналитическое значение данного показателя состоит в том, что при возрастающей скорости (и растущем уровне) темпы роста могут иметь тенденцию к уменьшению или оставаться без изменения. В результате абсолютное значение одного процента прироста будет расти. Следовательно, чтобы правильно оценить значение показателя темпа прироста, его нужно рассматривать не изолированно, а совместно с абсолютными показателями уровня и прироста. В статистической практике динамика стоимостных показателей оценивается с учетом уровня инфляции. Для анализа интенсивности изменения во времени одного явления по сравнению с другим рассчитывают коэффициент опережения (Коп). Он представляет собой отношение базисных темпов роста двух динамических рядов за одинаковые отрезки времени:
где К1 и К2 – базисные темпы роста соответственно первого и второго рядов динамики.
Коэффициент опережения показывает, во сколько раз быстрее растет уровень одного ряда динамики по сравнению с уровнем другого. При таком сопоставлении темпы должны характеризовать тенденции одного направления. Показатели динамики с переменной базой сравнения (цепные) используют для выявления типа изменения уровней ряда. В статистической практике в соответствии с показателями динамики различают следующие типы изменений: - равномерный рост или снижение (цепные абсолютные приросты одинаковы); - ускоренный рост или снижение (цепные приросты систематически увеличиваются по абсолютной величине); - замедленный рост или снижение (цепные приросты систематически уменьшаются тоже по абсолютной величине).
|



 ;
; ,
, - абсолютный прирост за t единиц времени;
- абсолютный прирост за t единиц времени; - текущий (сравниваемый) уровень ряда;
- текущий (сравниваемый) уровень ряда; - уровень ряда, непосредственно предшествующий текущему;
- уровень ряда, непосредственно предшествующий текущему; - уровень ряда, который принят за базу сравнения.
- уровень ряда, который принят за базу сравнения. ;
; .
. ;
; .
.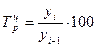 ;
; .
. ;
;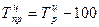 ;
; ;
; .
. .
. ,
,