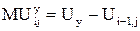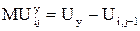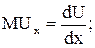ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Полезность и предельная полезность

Глава 3

ПОЛЕЗНОСТЬ И ПРЕДПОЧТЕНИЯ ПОТРЕБИТЕЛЯ

Полезность и предельная полезность

Важнейшей характеристикой рынка является кривая рыночного спроса. Эта кривая, в свою очередь, формируется на основе субъективных представлений потребителей о нужности, полезности для них данного товара.

В современной микроэкономике упрощенно полагают, что поведение потребителя полностью определяется его стремлением максимизировать некоторый показатель, который называют по-разному: удовольствие, наслаждение, удовлетворение, желаемость, ценность, польза и т. д. Мы будем следовать сложившейся традиции и использовать термин полезность.

Излагаемый в данном пункте подход к анализу поведения потребителей называют количественным (кардиналистским), поскольку он основан на предположении о возможности измерения различных благ в гипотетических единицах полезности. Такие оценки имеют исключительно индивидуальный, субъективный характер: один и тот же продукт может представлять большую ценность для одного потребителя и никакой — для другого. Поэтому количественный подход не предусматривает возможности сравнения и суммирования значений полезности для различных потребителей.

Те, кто критикуют количественный подход, предлагают порядковый (ординалистский) подход, который основывается на гораздо менее жестких предположениях. От потребителя не требуется измерять полезность благ в каких-либо единицах. Достаточно лишь, чтобы потребитель мог упорядочить все возможные товарные наборы по их «предпочтительности». Однако кардиналистский подход оказывается все же более плодотворным.

Величина полезности зависит от того, какие продукты и в каких объемах потреблены человеком (последовательность потребления не учитывается). Иными словами, полезность есть функция, зависящая от объемов потребления продуктов. Для двух продуктов она записывается в виде U(х;y), где U —полезность (utility — англ., полезность),х — объем потребления продукта X, y — объем потребления продукта Y.

Если количество потребленного продукта выражается целым числом, то такой продукт называют неделимым (конфеты, вишни). Если оба продукта неделимы, то говорят, что функция полезности дискретна, и ее записывают в виде U_y, где i — объем потребления продукта X, j — объем потребления продукта Y. Продукт называют делимым, если его количество может выражаться дробным числом (молоко, соль).

Предельная полезность продукта есть прирост полезности набора продуктов при увеличении объема потребления данного продукта на единицу. Предельную полезность обозначают через МU (marginal — англ., предельный, последний). Предельная полезность продукта зависит как от функции полезности, так и от исходного набора продуктов, к которому добавлена еще одна (последняя, маргинальная) единица.

Чтобы не путать предельную полезность с полезностью, полезность называют также общей полезностью и обозначают через TU.

Принцип убывающей предельной полезности (закон насыщения потребностей, первый закон Госсена) утверждает, что предельная полезность не возрастает. То есть с ростом потребления какого-то одного продукта (при неизменном объеме потребления всех остальных) общая полезность, получаемая потребителем, возрастает все более низкими темпами, а убывает — все более высокими темпами. Принцип убывающей предельной полезности теоретически подтверждается основным психофизиологическим законом Вебера-Фехнера, согласно которому раздражения равной интенсивности, повторяющиеся в течение определенного времени, сопровождаются снижением интенсивности ощущений.

Вначале рассмотрим понятие предельной полезности в простейшем случае, когда имеется лишь один продукт. Тогда функция полезности примет вид U(x).

Если продукт неделим, то предельная полезность i-й потребленной единицы продукта равна разности значений полезности после и до ее потребления:

MU_i = U_i – U_i_-1,

Если продукт делим, то предельная полезность х единиц продукта равна приросту общей полезности, приходящемуся на бесконечно малый «единичный» прирост потребления сверх объема х. Иными словами, в данном случае предельная полезность равна производной функции общей полезности:

На рис. 3.1 изображена функция полезности для случая, когда имеется один продукт. При увеличении потребления до величины х₁ предельная полезность убывает, оставаясь положительной (касательная к оси абсцисс имеет положительный наклон, который уменьшается). Функция полезности возрастает.

При объеме потребления, равном x₁, предельная полезность равна нулю, а общая полезность достигает своего максимального значения.

При увеличении объема потребления сверх величины x₁, предельная полезность становится отрицательной и продолжает убывать, увеличиваясь по модулю (касательная к оси абсцисс имеет отрицательный наклон).

При увеличении потребления сверх величины х₂, которой соответствует нулевая общая полезность, значение функции полезности становится отрицательным. В этом случае полезность характеризуют как «страдание», «антиполезность» и т. д.

Рис. 3.1 Полезность в случае одного продукта

Пример 1

Функция полезности U – х^0,5, где x — количество потребленных пряников. Найдем предельную полезность четвертого пряника.

Способ 1 (пряники делимы).

Дифференцируем функцию полезности:

MU(x) = 0,5 х^0,5

Подставляем х = 4, получаем MU (4) = 0,25.

Способ 2 (пряники неделимы).

MU₄ = U₄ – U₃ = 4^0,5 – 3⁰^,⁵ = 2 – 1,73 = 0,27.

Заметим, что ответы, полученные двумя способами, несколько различаются. Это связано с тем, что дискретная формула дает среднюю полезность целого четвертого пряника, а непрерывная формула — удельную полезность последней бесконечно малой его части, которая наименее «вкусна». Поэтому в непрерывном случае предельная полезность меньше.

Рассмотрим теперь понятие предельной полезности в случае, когда имеются два продукта. Тогда полезность задается функцией двух переменных.

Если продукты неделимы, то предельная полезность продукта X в наборе (i;j) равна:

Отметим, что в этом определении количество продукта Y в наборе, равное j, полагается неизменным. Аналогично предельная полезность продукта Y в наборе (i;j) равна:

Если продукты делимы, то предельные полезности выражаются частными производными функции полезности:

Пример 2

Функция полезности U = ху^0,5, где х — количество кофе (г), у — количество сливок (г). В чашке 60 г кофе и 25 г сливок. Найдем предельную полезность кофе и сливок.

Дифференцируем функцию полезности по х, считая y неизменным:

МU_х = у^0,5, отсюда МU_х = 5.

Дифференцируем функцию полезности по у, считая х неизменным:

MU_y =х × 0,5y^0,5, отсюда MU_y = 6.

Вывод: добавление в чашку 1 г сливок обеспечит данному потребителю больший прирост полезности, чем добавление 1 г кофе.

На рис. 3.2 дана геометрическая интерпретация функции полезности в случае двух продуктов. Некоторый набор продуктов (m; n) изображен точкой А на плоскости XOY. Полезность этого набора изображена точкой A_t, расположенной над точкой А на высоте, равной полезности данного набора U(m; n). Все такие точки образуют поверхность, которая является графиком функции полезности. Ее часто называют «горой удовольствий».

Рис. 3.2 Полезность в случае двух продуктов

Для того чтобы дать геометрическую иллюстрацию предельной полезности продукта X, через точку Л проведена плоскость параллельно оси ОХ (часть ее заштрихована). В пересечении этой плоскости и «горы удовольствий» образовалась кривая, аналогичная графику функции полезности в случае одного продукта (рис. 3.1). Угол наклона касательной к этой кривой характеризует величину предельной полезности продукта X.

Кривые безразличия

В предыдущем разделе мы рассмотрели способ «трехмерного» представления функции полезности для двух продуктов. В этом разделе мы рассмотрим более простой, «плоский» способ ее геометрического представления. Он заимствован из картографии: на географических картах точки местности, расположенные на одинаковой высоте над уровнем моря, соединяют линией, что позволяет достаточно наглядно показать рельеф земной поверхности.

Кривая безразличия есть изображение на плоскости множества наборов продуктов, имеющих одинаковую полезность. При выборе набора из такого множества потребитель не отдает предпочтения ни одному из них, ему «безразлично», какой из них взять.

Все кривые безразличия в совокупности образуют карту кривых безразличия.

Важнейшее свойство кривых безразличия состоит в том, что никакие две из них не пересекаются. Предположим все-таки, что нашлись две кривые безразличия, которые пересеклись в точке А, тогда все наборы обеих кривых имеют ту же полезность, что и набор А, а поэтому, согласно определению, они составляют вместе одну кривую безразличия. Наше предположение породило противоречие, поэтому оно неверно.

Другие свойства кривых безразличия зависят от того, продукты какого типа входят в набор. Если предельная полезность продукта положительна (добавление его в набор увеличивает полезность), то продукт называют благом, а если она отрицательна — то антиблагом. Рассмотрим три возможных варианта.

Рис. 3.3 Кривые безразличия:

а) благо-благо; б) благо-антиблаго; в) антиблаго-антиблаго

1. Оба продукта — блага. В этом случае кривые безразличия имеют отрицательный наклон и выпуклы к началу координат. Чем дальше расположена кривая безразличия от начала координат, тем большая полезность ей соответствует. Полезность положительна (рис. 3.3, а).

2. Один продукт — благо, другой — антиблаго. В этом случае кривые безразличия имеют положительный наклон и выпуклы к оси благ. Чем дальше расположена кривая безразличия от оси антиблага, тем большая полезность ей соответствует. Полезность может быть как положительной, так и отрицательной (рис. 3.3, б). Рассмотрим пример. Ольга любит черный кофе, поэтому добавление в него сливок уменьшает полезность напитка. Для нее кофе — благо (X), а сливки — антиблаго (Y). На рис. 3.3, б точки А и В изображают наборы с одинаковым количеством кофе, но в наборе А сливок больше. Поэтому для кривой безразличия а, расположенной «ближе» к оси сливок, полезность меньше, чем для кривой b. Множества наборов с положительной и отрицательной полезностью разделяет кривая безразличия, проходящая через начало координат. На этой кривой положительный эффект кофе полностью компенсируется отрицательным эффектом сливок, и полезность равна нулю.

3. Оба продукта — антиблага. В этом случае кривые безразличия имеют отрицательный наклон и вогнуты к началу координат. Чем дальше расположена кривая безразличия от начала координат, тем меньшая полезность ей соответствует. Полезность отрицательна (рис. 3.3, в).

Помимо основных случаев расположения кривых безразличия, представленных на рис. 3.3, имеется множество частных случаев. Рассмотрим три из них.

Рис. 3.4. Частные случаи кривых безразличия:

а) Y — нейтральное благо; б) блага смешанного типа; в) блага, образующие комплект

Нейтральное благо — продукт, добавление которого в набор не изменяет общей полезности, т. е. предельная полезность такого продукта равна нулю. В этом случае кривые безразличия имеют форму прямых, параллельных оси, отвечающей нейтральному благу.

На рис. 3.4,а нейтральным является продукт Y. Переход на новую кривую безразличия возможен только путем добавления в набор продукта X.

Благо смешанного типа — продукт, который при малом объеме потребления является благом, а при большом объеме — антиблагом. Практически все пищевые продукты относятся к этому типу: начиная с некоторого момента, наступает «переедание», и потребление дополнительной единицы продукта сокращает общую полезность. В этом случае кривые безразличия могут быть замкнутыми.

На рис. 3.4,б оба блага относятся к смешанному типу: X — хлеб, Y— молоко. На кривой безразличия а полезность меньше, чем на кривой b. Попробуем разобраться, почему. В точке А неполное удовлетворение связано с недостаточным количеством обоих продуктов («недоедание»). Оба продукта — блага. В точке В касательная к кривой безразличия параллельна оси ординат, т. е. молоко является нейтральным благом. Это связано с тем, что его в наборе непропорционально много по сравнению с хлебом. Эта непропорциональность и является причиной неполного удовлетворения в данной точке. В точке С неполное удовлетворение связано с эффектом «переедания», оба продукта являются антиблагами.

Блага, образующие комплект, — полезность набора определяется отношением объемов продуктов у/х. Если это отношение больше некоторого фиксированного числа γ, то продукт Y является нейтральным благом, а Х — нормальным благом. Наоборот, если отношение объемов меньше заданного числа, то X является нейтральным благом. В этом случае кривая безразличия представляет собой два взаимно перпендикулярных отрезка, пересекающихся в точке, у которой отношение ординаты и абсциссы равно γ.

Рассмотрим пример: X — правый ботинок, Y— левый ботинок (ботинки парные). В этом случае число правых и левых ботинок должно быть равным, поэтому γ равно единице. Если левых ботинок в наборе больше, чем правых (у/х > 1), то добавление еще одного левого не изменит полезности набора, т. е. левый ботинок — нейтральное благо. Наоборот, при избытке правых ботинок этот продукт является нейтральным благом. На рис. 3.4, в изображены две кривые безразличия, их вершины лежат на биссектрисе координатного угла, где отношение ординаты и абсциссы равно единице.