 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Уравнение Шредингера для кристалла
Возможные значения энергии электрона в кристалле можно найти из решения уравнения Шредингера для стационарных состояний, которое в общем случае имеет вид: HY = EY, (1.31) где H – оператор Гамильтона для кристалла, E – полная энергия кристалла, Y - волновая функция кристалла. Волновая функция Ψ(x,t) обычно определяется из выражения для плотности вероятности нахождения частицы в точке x в момент времени t. В общем случае волновая функция является комплексной величиной и имеет следующий вид:
Так как вероятность должна быть величиной действительной, то для нахождения плотности вероятности необходимо умножить Ψ(x,t) на комплексно сопряженную с ней функцию Ψ*(x,t). Комплексно-сопряженная волновая функция:
Определение Квадрат амплитуды волновой функции характеризует вероятность (P) нахождения электрона в данной точке пространства, определяемой радиус-вектором
или более точно: Квадрат модуля волновой функции, умноженный на элемент объема
Уравнение Шредингера должно быть дополнено ограничениями, накладываемыми на волновую функцию: - волновая функция должна быть конечной (так как вероятность не может быть больше 1), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком). - производные ¶Y/¶x, ¶Y/¶y, ¶Y/¶z должны быть непрерывны
Твердое тело представляет собой единую систему легких (электронов) и тяжелых (ядра) частиц. Наиболее полные сведения о свойствах такой системы, в том числе и об ее энергетическом спектре, можно получить решая уравнение Шредингера, соответствующее стационарным состояниям этой системы. Но, из-за того, что в кристалле имеет место большое число взаимодействий, уравнение Шредингера приобретает сложный вид:
В уравнение (2.3) входят следующие виды энергии: 1) Кинетическая энергия электронов: 2) Кинетическая энергия ядер: 3) Потенциальная энергия попарного взаимодействия электронов между собой: 4) Потенциальная энергия попарного взаимодействия ядер между собой:
5) Потенциальная энергия взаимодействия электронов с ядрами: где 6) Полная энергия кристалла E .
Уравнение (21) содержит 3N(Z+1) независимых переменных, где N – число атомов в кристалле, Zq0 – заряд ядра. Число атомов в 1 см3 составляет примерно 5*1022 и каждый атом содержит большое число электронов. Следовательно, волновая функция зависит от огромного числа (1024-1025) независимых переменных (в кремнии: 3N(Z+1) = 3 · 5х1022 · (14+1) = 2.25х1024 переменных). Точное решение уравнения Шредингера невозможно даже для отдельных атомов, за исключением атома водорода. Поэтому задача сводится к нахождению приближений в рамках физически оправданных упрощающих предположений. Зонная теория, лежащая в основе современной физики полупроводников, базируется на следующих основных приближениях: (а) Адиабатическое приближение (приближение Борна - Оппенгеймера) В его основе лежит тот факт, что масса ядер много больше, чем масса электронов (даже если бы кристалл состоял из самых легких атомов – атомов водорода, то M = mp = 1836 me). В равновесном состоянии средние значения кинетической энергии тех и других частиц одного порядка. Поэтому скорости движения электронов намного превосходят скорости ядер (для кремния, скорость электронов Ve превышает скорость ядра Vя в ~ 230 раз). При каждом изменении положения ядер практически мгновенно устанавливается пространственное распределение электронов, соответствующее новому положению ядер. Это позволяет в первом приближении рассматривать движение электронов в потенциальном поле фиксированных ядер. При изучении движения ядер, напротив, следует учитывать не мгновенное положение электронов, а поле, создаваемое их средним пространственным распределением. Таким образом суть адиабатического приближения состоит в том, что движение электронов и ядер можно считать независимым, происходящим без обмена энергией между электронной и ядерной подсистемами частиц. Следствия: а) Так как электронная и ядерная подсистемы независимы, то волновую функцию Y, как следует из теории вероятности, можно представить в виде произведения электронной Ye и ядерной
б) Если допустить, что ядра покоятся, тогда кинетическая энергия ядер обращается в нуль. в) Энергия взаимодействия электронов и ядер Vо принимает постоянное значение. Выбором начала отсчета энергии Vо можно обратить в нуль. Подстановка (1.42) в уравнение Шредингера (1.41) позволяет разделить уравнения Шредингера для ядер и для электронов и получить уравнение для электронов в виде:
где (б) Валентная аппроксимация. Поскольку состояние внутренних атомных электронов мало изменяется в кристаллической решетке, то можно ограничиться рассмотрением только валентных электронов, а под Несмотря на проведенные упрощения, уравнение (1.43) не может быть решено в общем виде, так как по-прежнему имеем дело с многоэлектронной задачей. Чтобы свести многоэлектронную задачу к одноэлектронной, для этого сделаем ещё одно допущение. (в) Одноэлектронное приближение (метод Хартри-Фока) Его суть заключается в том, что энергию попарного взаимодействия электронов заменяют энергией взаимодействия каждого электрона с усредненным полем всех остальных электронов. Это поле получило название самосогласованного, так как оно не только определяет движение данного электрона, но и само зависит от его движения. Введение самосогласованного поля позволяет рассматривать электроны в кристалле как невзаимодействующие частицы, т.е. движущиеся независимо друг от друга. Это является основанием для представления электронов проводимости в виде идеального газа и в уравнении (1.43) двойную сумму где После такой замены уравнение (1.43) распадается на сумму п одинаковых для всех электронов индивидуальных одноэлектронных уравнений вида
где Обозначив потенциальную энергию электрона в кристалле через функцию
уравнение (1.44) можно записать так:
а для одномерного случая:
Таким образом, в результате обоих приближений удалось свести задачу к обычному по форме уравнению Шредингера, но с другой функцией. В изолированном атоме, как известно, потенциальная фунция имеет вид гиперболы (см. рис. 1.38 и 1.41 (а)). В кристалле, соответственно, будет чередующийся ход таких гипербол, схематично изображенный на рис. 1.41. Обратите внимание, что наличие химических связей приводит к суперпозиции потенциалов, что сопровождается уменьшением средней амплитуды потенциального рельефа (рис. 1.41 (б) и (в)) Существуют различные способы рационального выбора вида функции V(r) для решения одноэлектронной задачи. Наиболее часто для этого используются состояние электрона, находящегося в потенциальном поле всех ионов решетки, заряд которых в среднем скомпенсирован зарядом валентных электронов.
Рис.1.41.Схематическое изображение потенциала одного атома (а), двух атомов, связанных химической связью (б), и периодического потенциала одномерной решётки (в).
Так как в кристалле атомы (атомные остатки, ионы) расположены строго периодически, то полный потенциал кристалла V(r) должен обладать трехмерной периодичностью. В общем случае, точный вид периодического потенциала V(r) неизвестен. Однако тот факт, что V(r) является периодической функцией, период которой совпадает с периодом кристаллической решетки, то есть: V(r) = V(r+g) (1.47) где g – вектор трансляции решетки (на рис. 1.41 -g=n·a, где n – целое число), позволяет получить два фундаментальных результата: Первый.Из условия трансляционной симметрии следует, что волновая функция электрона в точке rотличается от волновой функции электрона в точке r+g некоторым множителем С.
Из условия нормировки следует, что
Условию (1.49) можно удовлетворить, если положить С = exp(i·k·g) (1.50) {т. к. Здесь k-постоянный вектор, характеризующий квантовое состояние электрона в кристалле, называется волновым вектором. Вектор трансляции g имеет размерность длины, k·g- безразмерное, следовательно На основании соотношений (1.47) и (1.49), можно показать, что волновая функция электрона в кристалле имеет вид:
где Волны, описываемые соотношением (1.51), носят название волн Блоха. Волна Блоха представляет собой плоскую волну, модулированную периодической функцией Дополнительное пояснение. Выбор формы представления стационарной волновой функции электрона в кристалле в виде волны Блоха следует из периодичности кристаллической решетки, а именно, с учетом формул 1.48-1.50:
Где
Т.е. Таким образом: стационарная волновая функция электронов в периодическом поле кристалла зависит от волнового вектора Второй результат является следствием неоднозначности волнового вектора k для электрона в кристалле. Чтобы показать это, рассмотрим трансляционное условие:
Это условие не нарушится, если волновой вектор k заменить на вектор k+2pК, где
Где вектор К – вектор обратной решетки. Следовательно, состояния, характеризуемые волновым вектором k и k+ 2pК физически эквивалентны. То есть энергия электронов, находящихся в этих двух= состояниях одинакова. Другими словами, и волновая функция и энергия электрона в кристалле являются периодическими функциями волнового вектора k с периодом 2pК:
Если в k -пространстве (или в P-пространстве) построить обратную решетку, растянутую в 2p раз, то есть решетку с векторами 2pb1 , 2pb2 , 2pb3 (или Многогранник минимального объема, построенный вокруг начала координат в k-пространстве, содержащей все возможные различные состояния, называют первой или основной зоной Бриллюэна. С помощью векторов обратной решетки любую точку k -пространства можно перевести в первую зону Бриллюэна.
Рис. 1.42. Первая зона Бриллюэна для кристалла с простой кубической (а), кубической объемно-центрированной (б) и кубической гране-центрированной (в).
|



 (1.32)
(1.32)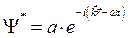 (1.33)
(1.33) .
. (1.34)
(1.34) есть вероятность обнаружить электрон в момент времени t в объеме
есть вероятность обнаружить электрон в момент времени t в объеме  , образующий бесконечно малую окрестность точки
, образующий бесконечно малую окрестность точки  .
. (1.40)
(1.40) Рис. 1.40. Плотность вероятности нахождения электрона в пространстве.
Рис. 1.40. Плотность вероятности нахождения электрона в пространстве.

 , где
, где  -постоянная Дирака (
-постоянная Дирака (  ), m-масса электрона, а
), m-масса электрона, а 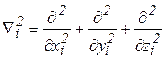 - оператор Лапласа для i-го электрона;
- оператор Лапласа для i-го электрона; , где
, где  -масса ядра;
-масса ядра;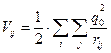 , где
, где  -заряд электрона, здесь i ≠ j(!)
-заряд электрона, здесь i ≠ j(!)
 ,
, - координаты электронов и ядер соответственно;
- координаты электронов и ядер соответственно; - собственная волновая функция кристалла, зависящая от координат всех электронов и атомных ядер.
- собственная волновая функция кристалла, зависящая от координат всех электронов и атомных ядер. волновых функций:
волновых функций: (1.42)
(1.42) (1.43)
(1.43) — координаты покоящихся ядер, E,
— координаты покоящихся ядер, E,  — соответственно энергия и волновая функция электронов.
— соответственно энергия и волновая функция электронов. подразумевать координаты не ядер, а атомных остатков. При этом уравнение (1.43) записывают только для валентных электронов, движущихся в потенциальном поле фиксированных атомных остатков.
подразумевать координаты не ядер, а атомных остатков. При этом уравнение (1.43) записывают только для валентных электронов, движущихся в потенциальном поле фиксированных атомных остатков. заменить суммой
заменить суммой  а
а  -суммой
-суммой 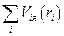 ,
, — потенциальная энергия i-го электрона в поле всех остальных электронов,
— потенциальная энергия i-го электрона в поле всех остальных электронов,  — потенциальная энергия i-го электрона в поле всех ядер.
— потенциальная энергия i-го электрона в поле всех ядер. , (1.44)
, (1.44) и Е— соответственно волновая функция и энергия электрона в кристалле.
и Е— соответственно волновая функция и энергия электрона в кристалле. равную
равную (1.45)
(1.45) ,(1.46)
,(1.46) . (1.47)
. (1.47)
 (1.48)
(1.48) (1.49)
(1.49) }
} и
и 
 , (1.51)
, (1.51) — периодическая функция,
— периодическая функция,  — плоская волна, идущая в направлении вектора k.
— плоская волна, идущая в направлении вектора k.

 функция
функция  обладает трехмерной периодичностью кристаллической решетки т. к., если взять любой произвольный вектор трансляции кристаллической решетки q1
обладает трехмерной периодичностью кристаллической решетки т. к., если взять любой произвольный вектор трансляции кристаллической решетки q1

 и имеет вид
и имеет вид  (1.52)
(1.52) . (1.53)
. (1.53) (1.54)
(1.54) (1.55)
(1.55) ,
,  ,
,  ) то все k -пространство можно разделить на области, в которых имеются физически эквивалентные состояния. Эти области называются зонами Бриллюэна.
) то все k -пространство можно разделить на области, в которых имеются физически эквивалентные состояния. Эти области называются зонами Бриллюэна.
