 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Энергия электрона в потенциальной яме с непроницаемыми стенками.
МОДЕЛи Энергетических зон Потенциальная энергия и импульс электрона в твердом теле определяются эффектами квантовых взаимодействий в системе сильно связанных электронов и атомов (ионов) полупроводника. Периодичность пространственного расположения атомов в кристалле, а, следовательно, и периодичность потенциала взаимодействия электронов с кристаллической решеткой, приводит к зонной структуре энергетического спектра электронов. Модель энергетических зон вводится для того, чтобы связать между собой энергию и импульс носителей заряда в кристалле. В настоящем разделе модель энергетических зон будет рассматриваться в двух вариантах – качественном и в более строгом, математическом. Модель позволяет описать распределение энергии электрона в твердых телах не только качественно, но и найти аналитическое выражение для энергии электронов путем решения уравнения Шрёдингера. Качественная модель зонной структуры твердого тела Важнейшей концепцией квантовой механики является представление о корпускулярно-волновом дуализме материи. Парадокс состоит в том, что частицы, например, электроны, являются одновременно частицами и волнами. Толкование этого парадокса может быть таким: волновая функция электрона (если на него не действуют силы) представляет собой бегущую синусоидальную волну, но если электрон каким-то образом обнаруживается в действительности, он регистрируется как реальная и вполне локализованная частица. Например, если пучок электронов проникает в кристалл при соответствующих энергетических и геометрических условиях, то волновая природа каждого отдельного электрона проявляется в его дифракции, как будто он и в самом деле является волной. Одновременно электрон может проявлять свою корпускулярную природу, которая проявляется в том, что электрон не производит частичного возбуждения большого количества частиц (атомов, электронов), хотя волновая функция электрона распространяется через весь кристалл. Более того, электрон внезапно появляется вблизи одного из атомов и полностью передает этому атому всю свою энергию, чего и следовало бы ожидать, если считать электрон классической частицей, упруго соударяющейся с атомом. Отличие этого эффекта от классического аналога заключается в том, что до столкновения электрона с определенным атомом нельзя предсказать, с каким именно атомом, расположенным вдоль фронта волновой функции, столкнется этот электрон. Подчеркнем, что если столкновение с атомом произошло, то в этом столкновении участвует весь электрон (целиком). Исходя из изложенного, рассмотрим зависимость энергии электрона от его импульса для различных условий потенциального взаимодействия с окружающей материей. 1. Энергия свободного электрона (электрон в вакууме):
Энергия электрона в потенциальной яме с непроницаемыми стенками.
|
, (1.28) частица волна где 
– постоянная Дирака, h – постоянная Планка (h =6,62х10-34 Дж·с), 
– волновой вектор, m, v и p – масса, скорость и импульс электрона. 
Рис. 1.36. Зависимость E от k для свободного электрона
Рис. 1.37. Дискретные Еn – уровни электрона в потенциальном ящике.
, или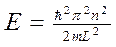 
, (1.29) где L-ширина потенциальной ямы, n = 1, 2, 3 …