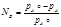ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Законы Рауля Вант-Гоффа. Эбуллиоскопия и криоскопия.

Условия протекания окислительно-восстановительной реакции. Уравнение Нернста.

Для установления протекания электродных процессов, расчета эдс и правильного написания уравнения самопроизвольно протекающей в гальваническом элементе реакции следует поступать следующим образом:

- С помощью таблицы стандартных электродных потенциалов записать уравнения реакций для каждого электрода с указанием значения электродного потенциала.

- Электродную реакцию с большим отрицательным или меньшим положительным (меньшим по модулю) значением потенциала переписать в обратном направлении (при этом знак потенциала следует изменить на противоположный).

- Под этим уравнением записать уравнение второй электродной реакции в том виде, в котором она дана в справочной таблице.

- Умножить коэффициенты при формулах веществ на такие числа, чтобы числа принятых и отданных электронов были равны (при этом электродные потенциалы не умножаются!).

- Суммируются оба уравнения и их электродные потенциалы.

Таким образом получается уравнение самопроизвольно протекающей электродной реакции. То есть условием протекания окислительно-восстановительной реакции является положительное значение суммарного электродного потенциала реакции.

Формула Нернста. Расчет потенциала и ЭДС при нестандартных условиях

Поскольку работа окислительно-восстановительной реакции равна изобарному потенциалу, взятому с обратным знаком,

G = -nEF

Изменения изобарного потенциала при стандартных и нестандартных условиях связаны соотношением:

где ПС – произведение концентрация продуктов реакции и исходных веществ в степени их стехиометрических коэффициентов. Подставляя G = -nEF, получаем:

Полученное уравнение для электродного потенциала окислительно-восстановительной реакции называется уравнением Нернста. Оно позволяет вычислять с помощью таблиц Е⁰ значение электродных потенциалов при нестандартных условиях (в том числе нестандартных концентраций).

Св-ва разбавленных р-ров неэлектролитов. Осмотическое давление. Закон Рауля.

Коллигативные свойства растворов – осмотическое давление, понижение давления пара, повышение температуры кипения (эбуллиоскопия), понижение температуры замерзания (криоскопия).

Осмотическое давление: осмос – явление самопроизвольного перехода растворителя через полупроницаемую перегородку в раствор. При этом объем раствора увеличивается и возникает осмотическое давление. Осмотическое давление зависит от концентрации растовренного вещества и температуры:  = СRT, где R – универсальная газовая постоянная.

Закон Рауля: относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества в растворе:

Законы Рауля Вант-Гоффа. Эбуллиоскопия и криоскопия.

Закон Вант-Гоффа: осмотическое давление равно тому давлению, которое нужно приложить к раствору, чтобы привести его в равновесие с чистым растворителем, отделенным от него полупроницаемой перепонкой.

Эбуллиоскопия: понижение давления насыщенного пара растворителя над раствором приводит к повышению температуры кипения: t_кип = EC (следствие из закона Рауля), где Е – эбуллиоскопическая постоянная. Для воды она равна 0,52. Зная повышения температуры кипения и эбуллиоскопическую постоянную для данного растворителя, можно определить концентрацию раствора.

Криоскопия: понижение давления насыщенного пара растворителя над раствором нелетучего вещества приводит к понижению температуры замерзания: t_зам = KC (следствие из закона Рауля), где К – криоскопическая постоянная. Для воды она равна 0,86.