 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ 12
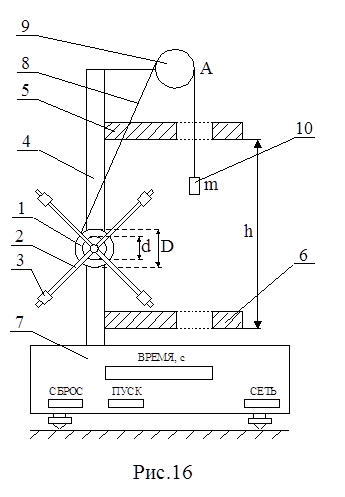
Экспериментальная установка показана на рис.16. Маятник Обербека состоит из четырех спиц, укрепленных на втулке под прямым углом друг к другу. На втулке закреплены два шкива 1 с разными диаметрами D и d. Втулка со спицами и шкивами может свободно вращаться относительно горизонтальной оси. Вдоль каждой спицы 2 можно перемещать грузик 3, закрепляя его на расстоянии R от оси вращения. Маятник Обербека и два кронштейна 5 и 6 крепятся к вертикальной стойке 4. Если на шкив 1 намотать нить 8, к ее концу присоединить груз 10 массой m и перекинуть нить через неподвижный блок 9, то, нажимая кнопку "ПУСК", измерить время ускоренного движения груза 10 на расстоянии h с помощью секундомера 7 экспериментальной установки.
На груз действует его сила тяжести
Момент силы натяжения, действующий на маятник Обербека, относительно горизонтальной оси z соответственно равен
Под действием момента силы маятник вращается с угловым
Подставляя формулы (14) и (15) в формулу (12), найдем общий момент инерции маятника Обербека относительно горизонтальной оси z, проходящей через центр масс маятника
Подставляя формулу (13) в формулу (16) и учитывая, что
Если момент инерции крестовины со шкивами относительно оси вращения обозначить Iкр, то общий момент инерции маятника относительно этой оси равен
Момент инерции IГ одного цилиндрического грузика относительно оси вращения находим с помощью формулы (10) и теоремы Штейнера (11):
где m1 - масса грузика, r, Н - радиус и высота цилиндрического грузика,
где Согласно формуле (20) меняя расстояние R центров грузиков до оси вращения, изменяем общий момент инерции I маятника Обербека.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Найдите массу m падающего груза и диаметры D и d шкивов. Установите и измерьте определенную высоту h падающего груза. Запишите найденные результаты в таблицу 1. 2. С помощью кнопки "СЕТЬ" включите экспериментальную установку. 3. Поместите на спицы маятника 4 грузика с массами m1 на одинаковом расстоянии R1 от центра шкива и добейтесь безразличного равновесия. Измерьте R1 и запишите в таблицу 1. 4. В один слой намотайте нить на шкиве с большим диаметром D. Отпустите крестовину и измерьте время падения t1D груза m с высоты h, нажимая кнопку "ПУСК". После измерения нажмите кнопку "СБРОС". Повторите эти измерения не менее пяти раз. Результаты запишите в таблицу 1. 5. Повторите измерения п.4, наматывая нить на шкив меньшего диаметра d, определяя время t1d. 6. Повторите измерения п.п.3¸5 для других расстояний R2, R3 и R4 грузиков до оси вращения. Результаты измерений запишите в таблицу 1. 7. Для каждого расстояния R и диаметра шкива найдите средние значения времени падения Таблица 1
8. Полуширину доверительного интервала
9. Для каждого диаметра шкива постройте график зависимости 10. По формулам (13) и (15) вычислите угловое ускорение 11. Для одного расстояния R1 по формулам (13), (14) и (15) оцените, как меняется угловое ускорение e при изменении момента силы, вызванном изменением радиуса r шкива.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте цель лабораторной работы. 2. Напишите основной закон динамики вращательного движения твердого тела относительно неподвижной оси. 3. Дайте определение момента силы относительно точки (центра). 4. Дайте определение момента силы относительно оси. 5. Найдите момент силы относительно оси Z, если модуль момента этой силы относительно точки О, лежащей на оси, равен М0 = 10 Нм, а направление момента образует с осью Z угол: 1) g = 30°; 2) g = 150°. 6. Модуль радиуса-вектора, проведенного из начала координат О в точку приложения силы, равен r = 30 см, а направление образует с направлением силы угол 7. Определите момент силы относительно точки, если модуль силы равен 8. Дайте определение момента инерции тела относительно оси. 9. По какой формуле можно вычислить момент инерции относительно оси: 10. На каком расстоянии от оси находится материальная точка массой 11. Моменты инерции относительно оси трех тел по отдельности равны 12. Какую массу имеет прямой круглый однородный цилиндр с радиусом основания R = 10 см, если момент инерции цилиндра относительно оси, проходящей через его центр масс параллельно боковой поверхности, равен 13. Сформулируйте теорему Штейнера. 14. Момент инерции однородного шара радиусом R = 6 см относительно оси, проходящей через центр шара, равен Iс. На каком расстоянии от центра шара должна находится ось, чтобы момент инерции шара относительно ее оказался равным 2Iс ? 15. Определите угловое ускорение твердого тела, вращающегося 16. Нарисуйте эскиз маятника Обербека. 17. Как можно менять момент инерции маятника Обербека ? 18. Момент какой силы сообщает маятнику Обербека угловое ускорение ? 19. Почему момент силы тяжести крестовины равен нулю ? 20. Какие силы действуют на груз, подвешенный к маятнику Обербека ? 21. Как найти силу натяжения нити, на которой подвешен груз ? 22. Как определить ускорение груза, подвешенного к маятнику Обербека ? 23. Как найти угловое ускорение крестовины ? 24. Выведите формулу экспериментального определения момента инерции маятника Обербека. 25. Какие величины постоянны при выполнении эксперимента в данной лабораторной работе ? 26. Как применить теорему Штейнера для теоретической оценки момента инерции маятника Обербека ? 27. Как меняется угловое ускорение маятника Обербека при удалении грузиков крестовины от оси вращения ? 28. Меняется ли натяжение нити в зависимости от расстояния грузиков крестовины от оси вращения? 29. Как меняется угловое ускорение крестовины при изменении радиуса r ее шкива ? 30. Выведите формулу вычисления доверительного интервала DI при экспериментальном определении момента инерции I маятника Обербека.
12 |



 Так как начальная скорость груза равна нулю, то
Так как начальная скорость груза равна нулю, то  ,
, . (13)
. (13) и сила натяжения нити
и сила натяжения нити  . Если на вертикальной оси координат положительное направление выбрать вниз, то проекция второго закона Ньютона
. Если на вертикальной оси координат положительное направление выбрать вниз, то проекция второго закона Ньютона  на эту ось имеет вид:
на эту ось имеет вид:  . Отсюда сила натяжения нити равна
. Отсюда сила натяжения нити равна .
. , где r - радиус шкива. Тогда
, где r - радиус шкива. Тогда . (14)
. (14) . Отсюда
. Отсюда . (15)
. (15) . (16)
. (16) . (17)
. (17) . (18)
. (18) , (19)
, (19) , (20)
, (20) .
. груза, а также полуширину доверительного интервала Dt. По формуле (15) вычислите момент инерции I маятника Обербека в каждом случае.
груза, а также полуширину доверительного интервала Dt. По формуле (15) вычислите момент инерции I маятника Обербека в каждом случае.

 . (21)
. (21)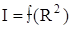 .
. для различных R и постройте график зависимости
для различных R и постройте график зависимости  для каждого диаметра шкива. Пренебрегая погрешностями измерения D и h, найдите полуширину De доверительного интервала с помощью формулы:
для каждого диаметра шкива. Пренебрегая погрешностями измерения D и h, найдите полуширину De доверительного интервала с помощью формулы:  .
.