 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ 12
Лабораторная работа № 5 ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ
ЦЕЛЬ РАБОТЫ Изучение характеристик вращательного движения твердого тела. Применение основного закона динамики вращательного движения для определения момента инерции тела.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z
аналогично второму закону Ньютона F = ma. В формуле (1) Мz - момент внешних сил, действующих на тело относительно оси z;
Модуль вектора
где h = r×sina - плечо силы, которое равно длине перпендикуляра, опущенного из точки О на направление силы. Вектор Момент силы относительно оси z равен проекции на эту ось момента силы относительно произвольной точки О, лежащей на оси z:
Момент силы Мz относительно оси - величина алгебраическая. Кроме формулы (4) для вычисления момента силы относительно оси z можно использовать формулу:
где Момент инерции тела Iz относительно оси z является мерой инертности тела при его вращении относительно этой оси и определяется формулой:
где Из формулы (6) видно, что момент инерции тела относительно оси равен сумме моментов инерции
Предел суммы (7) при
С помощью формулы (8) можно вычислять моменты инерции однородных тел правильной геометрической формы относительно осей, проходящих через центры масс этих тел. В частности, момент инерции однородного прямого круглого цилиндра массой m и радиусом основания R относительно оси z, проходящей через центр масс С этого цилиндра параллельно его боковой поверхности (рис.14а), равен
Если же ось z перпендикулярна боковой поверхности такого цилиндра (рис.14б), то момент инерции можно найти по формуле
где R - радиус основания, Н - высота цилиндра. Для вычисления момента инерции тела относительно произвольной оси z¢ применяется теорема Штейнера (рис.15): момент инерции тела I относительно произвольной оси z¢ равен сумме момента инерции Iс относительно оси z, параллельной данной оси z¢ и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
Момент инерции тела сложной формы проще определить экспериментально. Из уравнения (1) получим
Момент инерции тела Iz можно найти по формуле (12), если экспериментально оценить момент сил Mz и угловое ускорение e.
12 |



 (1)
(1)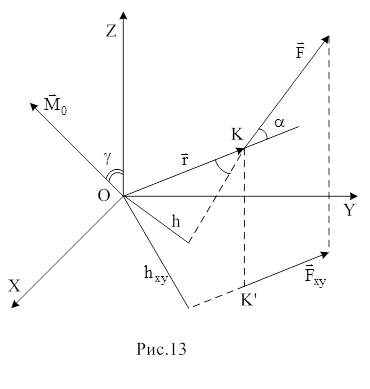 Момент силы характеризует вращательное действие силы. Различают момент силы относительно точки (центра) и момент силы относительно оси. Моментом силы (см.рис.13) относительно точки О называется вектор
Момент силы характеризует вращательное действие силы. Различают момент силы относительно точки (центра) и момент силы относительно оси. Моментом силы (см.рис.13) относительно точки О называется вектор  , равный векторному произведению силы
, равный векторному произведению силы  и радиуса - вектора
и радиуса - вектора  , проведенного из точки О в точку К приложения силы:
, проведенного из точки О в точку К приложения силы: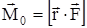 . (2)
. (2) , (3)
, (3) и
и  . (4)
. (4) , (5)
, (5) - проекция силы
- проекция силы  , (6)
, (6) - масса материальной точки, удаленной на расстояние Ri от оси z.
- масса материальной точки, удаленной на расстояние Ri от оси z. отдельных материальных точек тела. Если массу
отдельных материальных точек тела. Если массу  выразить через плотность тела r и объема
выразить через плотность тела r и объема  . (7)
. (7) - это интеграл по объему тела V:
- это интеграл по объему тела V: . (8)
. (8) . (9)
. (9) , (10)
, (10)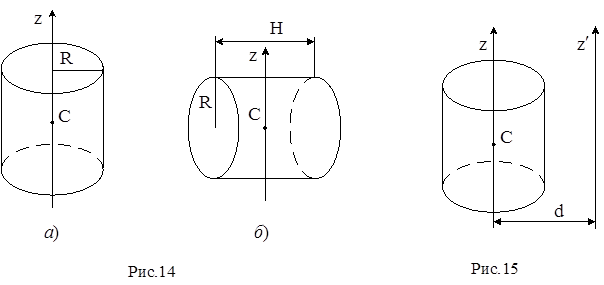
 . (11)
. (11) . (12)
. (12)