 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Решение обобщенного уравнения состояния
Электрической системы Электрическая система - это электрическая часть энергетической системы, т.е. совокупность элементов, вырабатывающих, преобразующих, передающих, распределяющих и потребляющих электрическую энергию. Состояние системы в любой момент времени называется режимом системы. Параметры режима - это показатели, зависящие от изменения режима. К ним относятся напряжения в различных точках системы, токи в ее элементах, ЭДС, мощности и т.д. Параметры режима будем отмечать точками над буквами (например,  ). ). Различают переходный и установившийся режимы электрической системы. В переходном процессе параметры режима изменяются во времени и связаны между собой системой дифференциальных уравнений. Установившийся режим характеризуется параметрами, которые не изменяются со временем и при использовании символического метода являются комплексными величинами, связанными между собой системой алгебраических комплексных уравнений. Математическим описанием установившегося режима являются уравнения состояния электрической цепи, основанные на законах Ома и Кирхгофа. В этих уравнениях параметры режима связаны между собой коэффициентами пропорциональности, которые называются параметрами системы и зависят от свойств элементов системы и от способов соединения их между собой. К ним относятся полные, активные и реактивные сопротивления, собственные и взаимные проводимости элементов и т.д. Параметры системы будем обозначать без точки над буквами (например,  ). Обычно считают, что параметры системы не зависят от параметров режима, т.е. система является линейной. В общем случае параметры системы могут зависеть от изменений ее режима и тогда система называется нелинейной. Кроме того, в энергосистеме всегда присутствует нелинейность, обусловленная характером соотношений между параметрами ее режима. Например, потребляемая в сопротивлении мощность связана квадратичной зависимостью с напряжением. Поэтому, если в качестве исходных параметров принимаются мощности в узлах цепи, то уравнения состояния оказываются нелинейными. ). Обычно считают, что параметры системы не зависят от параметров режима, т.е. система является линейной. В общем случае параметры системы могут зависеть от изменений ее режима и тогда система называется нелинейной. Кроме того, в энергосистеме всегда присутствует нелинейность, обусловленная характером соотношений между параметрами ее режима. Например, потребляемая в сопротивлении мощность связана квадратичной зависимостью с напряжением. Поэтому, если в качестве исходных параметров принимаются мощности в узлах цепи, то уравнения состояния оказываются нелинейными. Исследование электрической системы начинается с составления ее схемы замещения, которая представляет собой совокупность схем замещения ее отдельных элементов, соединенных между собой в той же последовательности, что и в реальной схеме. При рассмотрении симметричных установившихся режимов системы трехфазного переменного тока все величины, характеризующие схемы замещения ее элементов, являются комплексными. При этом схемы замещения составляются на одну фазу с нейтралью. Отдельные элементы электрической системы представляются схемами замещения, состоящими из элементов электрической цепи - источников напряжения или тока и сопротивлений. Источники электроэнергии могут быть представлены в схеме замещения либо в виде источника напряжения с ЭДС  и внутренним сопротивлением и внутренним сопротивлением  , либо в виде источника тока , либо в виде источника тока  , который обычно называют задающим током. Нагрузки (т.е. потребители электроэнергии) имеют схему замещения либо в виде сопротивления , который обычно называют задающим током. Нагрузки (т.е. потребители электроэнергии) имеют схему замещения либо в виде сопротивления  , либо в виде задающего тока , либо в виде задающего тока  . Линии электропередачи, трансформаторы подстанций и электростанций представляются в схеме замещения системы в виде сопротивлений, причем схемы замещения трансформаторов могут быть объединены со схемами замещения соответствующих источников питания и нагрузок. Таким образом, схему замещения электрической системы можно представить в виде электрической цепи, содержащей ветви, узлы и контуры. В узлах цепи подключены генераторы или нагрузки. Ветвью называется участок цепи, который состоит из последовательно соединенных ЭДС и сопротивления (или только сопротивления) и вдоль которого в любой заданный момент времени ток имеет одно и то же значение. Узел - это точка соединения двух или более ветвей. Контур - это участок цепи, образованный таким последовательным соединением нескольких ветвей, при котором начало первой ветви контура соединено с концом последней в одном узле. Схема, содержащая контуры, называется замкнутой. При отсутствии контуров схема замещения называется разомкнутой. . Линии электропередачи, трансформаторы подстанций и электростанций представляются в схеме замещения системы в виде сопротивлений, причем схемы замещения трансформаторов могут быть объединены со схемами замещения соответствующих источников питания и нагрузок. Таким образом, схему замещения электрической системы можно представить в виде электрической цепи, содержащей ветви, узлы и контуры. В узлах цепи подключены генераторы или нагрузки. Ветвью называется участок цепи, который состоит из последовательно соединенных ЭДС и сопротивления (или только сопротивления) и вдоль которого в любой заданный момент времени ток имеет одно и то же значение. Узел - это точка соединения двух или более ветвей. Контур - это участок цепи, образованный таким последовательным соединением нескольких ветвей, при котором начало первой ветви контура соединено с концом последней в одном узле. Схема, содержащая контуры, называется замкнутой. При отсутствии контуров схема замещения называется разомкнутой. Основная трудность при исследовании сложных электрических систем заключается в составлении и решении большого количества уравнений состояния. Для упрощения этой процедуры используют теорию графов и матричную алгебру. Конфигурацию схемы замещения можно отобразить в виде графа. Граф представляет собой совокупность вершин и ребер, соединяющих некоторые (или все) пары вершин. Любая часть графа называется подграфом. Если в графе можно выбрать путь, который соединяет любые две его вершины, то этот граф является связанным; иначе - несвязанным. Если ребра графа имеют фиксированные направления, то граф называется направленным. Наименьший связанный подграф, содержащий все вершины графа и не содержащий контуры, называется деревом. Ветви, не вошедшие в дерево графа, называются хордами. Схема замещения электрической системы обычно является связанным направленным графом, ребрами которого служат ветви, а вершинами - узлы. Направление ветви от начального узла к конечному узлу обозначается стрелкой и является положительным направлением в этой ветви ЭДС  , тока , тока  и падения напряжения и падения напряжения  . Условимся нумеровать ветви просто цифрами, узлы - цифрами, заключенными в окружности, а контуры - цифрами в прямоугольниках. Один из узлов выбирается в качестве балансирующего и обозначается цифрой 0 (см. рис.1). . Условимся нумеровать ветви просто цифрами, узлы - цифрами, заключенными в окружности, а контуры - цифрами в прямоугольниках. Один из узлов выбирается в качестве балансирующего и обозначается цифрой 0 (см. рис.1). 
Рис. 1. Граф схемы замещения электрической системы Топологию графа схемы замещения описывает матрица соединений ветвей в узлах или первая матрица инциденций:  (1) (1)
где  - число независимых узлов (без учета балансирующего узла), а - число независимых узлов (без учета балансирующего узла), а  - число ветвей. Строки матрицы - число ветвей. Строки матрицы  соответствуют узлам графа, а столбцы - ветвям. Элемент соответствуют узлам графа, а столбцы - ветвям. Элемент  равен: +1, если узел равен: +1, если узел  является начальной вершиной ветви является начальной вершиной ветви  ; -1, если узел ; -1, если узел  является конечной вершиной ветви является конечной вершиной ветви  ; 0, если узел ; 0, если узел  не является вершиной ветви не является вершиной ветви  . Для графа, изображенного на рис. 1, . Для графа, изображенного на рис. 1,  . (2) . (2)
Матрица  позволяет компактно записать уравнения первого закона Кирхгофа: позволяет компактно записать уравнения первого закона Кирхгофа:  , (3) , (3)
где 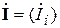 - столбец токов в ветвях ( - столбец токов в ветвях (  ), а ), а  - столбец задающих токов в узлах ( - столбец задающих токов в узлах (  ). ). Для графа на рис. 1 матричное уравнение (3) в развернутом виде есть:  . (4) . (4)
Информацию о контурах графа схемы замещения содержит вторая матрица инциденций или матрица соединений ветвей в независимые контуры:  (5) (5)
где  - число независимых контуров в схеме, связанное с числом ветвей - число независимых контуров в схеме, связанное с числом ветвей  и числом независимых узлов и числом независимых узлов  соотношением: соотношением:  (6) (6)
Строки матрицы  соответствуют независимым контурам, а столбцы - ветвям. Элемент соответствуют независимым контурам, а столбцы - ветвям. Элемент  равен: +1, если ветвь равен: +1, если ветвь  входит в контур входит в контур  и их направления совпадают; -1, если ветвь и их направления совпадают; -1, если ветвь  входит в контур входит в контур  и их направления противоположны; 0, если ветвь и их направления противоположны; 0, если ветвь  не входит в контур не входит в контур  . . Чтобы найти матрицу  , необходимо выбрать независимые контуры, причем количество вариантов такого выбора обычно велико. Например, граф на рис. 1 содержит три контура, но только два из них независимы (l=6-4=2) и выбрать их можно тремя способами (число сочетаний , необходимо выбрать независимые контуры, причем количество вариантов такого выбора обычно велико. Например, граф на рис. 1 содержит три контура, но только два из них независимы (l=6-4=2) и выбрать их можно тремя способами (число сочетаний  ). Сделать однозначный выбор независимых контуров в схеме и составить матрицу ). Сделать однозначный выбор независимых контуров в схеме и составить матрицу  можно по следующему алгоритму. можно по следующему алгоритму. Матрицы  и и  связаны соотношением: связаны соотношением:  , (7) , (7)
где  - транспонированная матрица - транспонированная матрица  , а , а  - нулевая матрица размерностью - нулевая матрица размерностью  . Разобьем матрицы . Разобьем матрицы  и и  на блоки, соответствующие дереву и хордам графа: на блоки, соответствующие дереву и хордам графа:  , (8) , (8)
где  - квадратная матрица размерностью - квадратная матрица размерностью  , ,  - прямоугольная матрица размерностью - прямоугольная матрица размерностью  , ,  - прямоугольная матрица размерностью - прямоугольная матрица размерностью  и и  - квадратная матрица размерностью - квадратная матрица размерностью 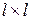 . Матрицы . Матрицы  и и  относятся к дереву графа, а относятся к дереву графа, а  и и  - к хордам, причем число хорд равно числу независимых контуров в схеме - к хордам, причем число хорд равно числу независимых контуров в схеме  . В качестве хорд удобно выбрать ветви с наибольшими номерами (ветви 5 и 6 на рис. 1). . В качестве хорд удобно выбрать ветви с наибольшими номерами (ветви 5 и 6 на рис. 1). Теперь уравнение (7) можно записать в виде:  . (9) . (9)
Матрица 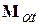 - квадратная порядка - квадратная порядка  и неособенная (ее определитель не равен нулю), поэтому обратная ей матрица и неособенная (ее определитель не равен нулю), поэтому обратная ей матрица  существует и из уравнения (9) следует, что существует и из уравнения (9) следует, что 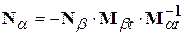 . (10) . (10)
Можно доказать, что для любой схемы замещения имеется такая система независимых контуров, для которой  является единичной матрицей порядка является единичной матрицей порядка  . Такая система называется системой базисных контуров и для нее выполняется условие: . Такая система называется системой базисных контуров и для нее выполняется условие:  , (11) , (11)
где символ  обозначает единичную матрицу размерностью обозначает единичную матрицу размерностью 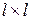 . . Таким образом, с помощью соотношений (11) по известной первой матрице инциденций  можно определить вторую матрицу инциденций можно определить вторую матрицу инциденций  , соответствующую системе базисных контуров. , соответствующую системе базисных контуров. Для графа на рис. 1 разбиение матрицы  на блоки на блоки  , ,  и их последующее транспонирование дает: и их последующее транспонирование дает:  , ,
 . .
Обратную матрицу  найдем методом Гаусса. Для этого сформируем объединенную прямоугольную матрицу путем добавления к матрице найдем методом Гаусса. Для этого сформируем объединенную прямоугольную матрицу путем добавления к матрице  справа единичной матрицы того же порядка: справа единичной матрицы того же порядка:  . .
Выполняя преобразования над строками этой матрицы в соответствии с алгоритмом метода Гаусса, переместим единичный блок из правой части в левую часть матрицы. Тогда правая квадратная часть этой объединенной мат-рицы и будет обратной матрицей  . . На первом шаге умножим первую и вторую строки матрицы на –1:  . .
Вычтем из третьей строки первую, а из четвертой - вторую:  . .
Умножим третью и четвертую строки матрицы на -1: 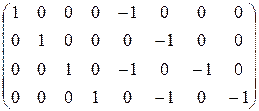 . .
Следовательно,  . .
Применяя формулы (8), получим:  , ,
 . .
Таким образом, искомая вторая матрица инциденций  , соответствующая системе базисных контуров, имеет вид: , соответствующая системе базисных контуров, имеет вид:  . (12) . (12)
Полученной матрице  соответствуют базисные контуры 1 и 2, показанные на рис. 1. соответствуют базисные контуры 1 и 2, показанные на рис. 1. Используя матрицу  , второй закон Кирхгофа можно записать в следующей матричной форме: , второй закон Кирхгофа можно записать в следующей матричной форме:  , (13) , (13)
где  - столбец падений напряжений на ветвях схемы ( - столбец падений напряжений на ветвях схемы (  ). Для графа на рис. 1 матричное уравнение (13) в развернутом виде есть: ). Для графа на рис. 1 матричное уравнение (13) в развернутом виде есть:  . (14) . (14)
Запишем закон Ома в матричной форме:  , (15) , (15)
где  - столбец ЭДС в ветвях ( - столбец ЭДС в ветвях (  ), а ), а  - матрица сопротивлений ветвей ( - матрица сопротивлений ветвей (  ). Если между ветвями отсутствует взаимоиндуктивная связь, то матрица ). Если между ветвями отсутствует взаимоиндуктивная связь, то матрица  является диагональной матрицей порядка является диагональной матрицей порядка  . . Комбинируя (13) и (15), получим:  , (16) , (16)
где  . (17) . (17)
Здесь  - это столбец контурных ЭДС, представляющих собой суммы ЭДС ветвей, входящих в каждый контур ( - это столбец контурных ЭДС, представляющих собой суммы ЭДС ветвей, входящих в каждый контур (  ). ). Уравнения (3) и (16) можно заменить одним матричным уравнением, если матрицы  и и  рассматривать как блоки одной объединенной матрицы: рассматривать как блоки одной объединенной матрицы:  , (18) , (18)
а столбцы  и и  рассматривать как один объединенный столбец рассматривать как один объединенный столбец  . (19) . (19)
Здесь  - квадратная матрица порядка - квадратная матрица порядка  , называемая матрицей параметров схемы замещения системы, а , называемая матрицей параметров схемы замещения системы, а  - столбец, содержащий - столбец, содержащий  элементов и называемый столбцом исходных параметров режима. элементов и называемый столбцом исходных параметров режима. В результате получаем одно матричное уравнение, которое называется обобщенным уравнением состояния электрической системы:  . (20) . (20)
Для графа на рис. 1 в предположении диагональности матрицы  обобщенное уравнение состояния в развернутом виде есть: обобщенное уравнение состояния в развернутом виде есть:  , (21) , (21)
где  и и  . . Токи в ветвях  можно найти либо путем обращения матрицы можно найти либо путем обращения матрицы  и применения уравнения: и применения уравнения:  , (22) , (22)
либо путем решения системы линейных уравнений (20) методом последовательного исключения неизвестных (методом Гаусса), который является более эффективным в вычислительном отношении для сложных схем замещения. Коль скоро токи в ветвях  найдены, можно определить напряжения в ветвях согласно уравнению закона Ома (15). найдены, можно определить напряжения в ветвях согласно уравнению закона Ома (15). Обозначим напряжение узла  через через  , а напряжение балансирующего узла - через , а напряжение балансирующего узла - через  . Тогда . Тогда  , (23) , (23)
где  - столбец узловых напряжений, а - столбец узловых напряжений, а  - столбец узловых напряжений относительно балансирующего узла ( - столбец узловых напряжений относительно балансирующего узла (  ), связанный со столбцом падений напряжений на ветвях соотношением: ), связанный со столбцом падений напряжений на ветвях соотношением:  . (24) . (24)
Матрица  - прямоугольная и ее нельзя обратить. Чтобы найти - прямоугольная и ее нельзя обратить. Чтобы найти  , необходимо разбить матрицу , необходимо разбить матрицу  и столбец и столбец  на блоки, соответствующие дереву и хордам графа: на блоки, соответствующие дереву и хордам графа:  . (25) . (25)
Отсюда  (26) (26)
и  , (27) , (27)
где матрица  уже была найдена раньше при определении второй матрицы инциденций уже была найдена раньше при определении второй матрицы инциденций  . . Определив по уравнению (27) относительные узловые напряжения  , можно затем найти абсолютные узловые напряжения , можно затем найти абсолютные узловые напряжения  . (28) . (28)
Обозначим через  столбец узловых мощностей ( столбец узловых мощностей (  ). Элементы этого столбца можно найти из соотношений: ). Элементы этого столбца можно найти из соотношений:  , (29) , (29)
где  - комплексно-сопряженный задающий ток в - комплексно-сопряженный задающий ток в  -ом узле. В уравнениях (29) мощность трехфазной цепи определяется фазными значениями напряжений и токов. При использовании линейных узловых напряжений мощности узлов определяются как -ом узле. В уравнениях (29) мощность трехфазной цепи определяется фазными значениями напряжений и токов. При использовании линейных узловых напряжений мощности узлов определяются как  . .
|




 ).
). ). Обычно считают, что параметры системы не зависят от параметров режима, т.е. система является линейной. В общем случае параметры системы могут зависеть от изменений ее режима и тогда система называется нелинейной. Кроме того, в энергосистеме всегда присутствует нелинейность, обусловленная характером соотношений между параметрами ее режима. Например, потребляемая в сопротивлении мощность связана квадратичной зависимостью с напряжением. Поэтому, если в качестве исходных параметров принимаются мощности в узлах цепи, то уравнения состояния оказываются нелинейными.
). Обычно считают, что параметры системы не зависят от параметров режима, т.е. система является линейной. В общем случае параметры системы могут зависеть от изменений ее режима и тогда система называется нелинейной. Кроме того, в энергосистеме всегда присутствует нелинейность, обусловленная характером соотношений между параметрами ее режима. Например, потребляемая в сопротивлении мощность связана квадратичной зависимостью с напряжением. Поэтому, если в качестве исходных параметров принимаются мощности в узлах цепи, то уравнения состояния оказываются нелинейными. и внутренним сопротивлением
и внутренним сопротивлением  , либо в виде источника тока
, либо в виде источника тока  , который обычно называют задающим током. Нагрузки (т.е. потребители электроэнергии) имеют схему замещения либо в виде сопротивления
, который обычно называют задающим током. Нагрузки (т.е. потребители электроэнергии) имеют схему замещения либо в виде сопротивления  и падения напряжения
и падения напряжения  . Условимся нумеровать ветви просто цифрами, узлы - цифрами, заключенными в окружности, а контуры - цифрами в прямоугольниках. Один из узлов выбирается в качестве балансирующего и обозначается цифрой 0 (см. рис.1).
. Условимся нумеровать ветви просто цифрами, узлы - цифрами, заключенными в окружности, а контуры - цифрами в прямоугольниках. Один из узлов выбирается в качестве балансирующего и обозначается цифрой 0 (см. рис.1).
 (1)
(1) - число независимых узлов (без учета балансирующего узла), а
- число независимых узлов (без учета балансирующего узла), а  - число ветвей. Строки матрицы
- число ветвей. Строки матрицы  соответствуют узлам графа, а столбцы - ветвям. Элемент
соответствуют узлам графа, а столбцы - ветвям. Элемент  равен: +1, если узел
равен: +1, если узел  является начальной вершиной ветви
является начальной вершиной ветви  ; -1, если узел
; -1, если узел  . (2)
. (2) , (3)
, (3)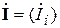 - столбец токов в ветвях (
- столбец токов в ветвях (  ), а
), а  - столбец задающих токов в узлах (
- столбец задающих токов в узлах (  ).
). . (4)
. (4) (5)
(5) - число независимых контуров в схеме, связанное с числом ветвей
- число независимых контуров в схеме, связанное с числом ветвей  (6)
(6) соответствуют независимым контурам, а столбцы - ветвям. Элемент
соответствуют независимым контурам, а столбцы - ветвям. Элемент  равен: +1, если ветвь
равен: +1, если ветвь  ). Сделать однозначный выбор независимых контуров в схеме и составить матрицу
). Сделать однозначный выбор независимых контуров в схеме и составить матрицу  , (7)
, (7) - транспонированная матрица
- транспонированная матрица  - нулевая матрица размерностью
- нулевая матрица размерностью  . Разобьем матрицы
. Разобьем матрицы  , (8)
, (8) - квадратная матрица размерностью
- квадратная матрица размерностью  ,
,  - прямоугольная матрица размерностью
- прямоугольная матрица размерностью  ,
,  - прямоугольная матрица размерностью
- прямоугольная матрица размерностью  - квадратная матрица размерностью
- квадратная матрица размерностью 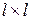 . Матрицы
. Матрицы  . (9)
. (9)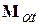 - квадратная порядка
- квадратная порядка  существует и из уравнения (9) следует, что
существует и из уравнения (9) следует, что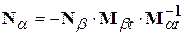 . (10)
. (10) , (11)
, (11) обозначает единичную матрицу размерностью
обозначает единичную матрицу размерностью  ,
, .
. справа единичной матрицы того же порядка:
справа единичной матрицы того же порядка: .
. .
. .
. .
.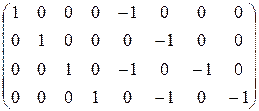 .
. .
. ,
, .
. . (12)
. (12) , (13)
, (13) - столбец падений напряжений на ветвях схемы (
- столбец падений напряжений на ветвях схемы (  ). Для графа на рис. 1 матричное уравнение (13) в развернутом виде есть:
). Для графа на рис. 1 матричное уравнение (13) в развернутом виде есть: . (14)
. (14) , (15)
, (15) - столбец ЭДС в ветвях (
- столбец ЭДС в ветвях (  - матрица сопротивлений ветвей (
- матрица сопротивлений ветвей (  ). Если между ветвями отсутствует взаимоиндуктивная связь, то матрица
). Если между ветвями отсутствует взаимоиндуктивная связь, то матрица  является диагональной матрицей порядка
является диагональной матрицей порядка  , (16)
, (16) . (17)
. (17) - это столбец контурных ЭДС, представляющих собой суммы ЭДС ветвей, входящих в каждый контур (
- это столбец контурных ЭДС, представляющих собой суммы ЭДС ветвей, входящих в каждый контур (  ).
). рассматривать как блоки одной объединенной матрицы:
рассматривать как блоки одной объединенной матрицы: , (18)
, (18) и
и  рассматривать как один объединенный столбец
рассматривать как один объединенный столбец . (19)
. (19) - квадратная матрица порядка
- квадратная матрица порядка  - столбец, содержащий
- столбец, содержащий  . (20)
. (20) , (21)
, (21) и
и  .
. можно найти либо путем обращения матрицы
можно найти либо путем обращения матрицы  , (22)
, (22) , а напряжение балансирующего узла - через
, а напряжение балансирующего узла - через  . Тогда
. Тогда , (23)
, (23) - столбец узловых напряжений, а
- столбец узловых напряжений, а  - столбец узловых напряжений относительно балансирующего узла (
- столбец узловых напряжений относительно балансирующего узла (  ), связанный со столбцом падений напряжений на ветвях соотношением:
), связанный со столбцом падений напряжений на ветвях соотношением: . (24)
. (24) , необходимо разбить матрицу
, необходимо разбить матрицу  на блоки, соответствующие дереву и хордам графа:
на блоки, соответствующие дереву и хордам графа: . (25)
. (25) (26)
(26) , (27)
, (27) уже была найдена раньше при определении второй матрицы инциденций
уже была найдена раньше при определении второй матрицы инциденций  , можно затем найти абсолютные узловые напряжения
, можно затем найти абсолютные узловые напряжения . (28)
. (28) столбец узловых мощностей (
столбец узловых мощностей (  ). Элементы этого столбца можно найти из соотношений:
). Элементы этого столбца можно найти из соотношений: , (29)
, (29) - комплексно-сопряженный задающий ток в
- комплексно-сопряженный задающий ток в  .
.