 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Достаточные условия экстремума. 12
Лекция 22. Условия возрастания и убывания функции. Экстремумы функции, необходимое условие. Достаточные условия. Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке. В предыдущих лекциях использовались известные из курса элементарной математики понятия возрастающей и убывающей функций. Определим их еще раз. Определение 22.1. Функция y = f(x) называется возрастающей (убывающей) на [ab], если
Теорема 22.1. Если функция f(x), дифференцируемая на [ab], возрастает на этом отрезке, то Если f(x) непрерывна на [ab] и дифференцируема на (ab), причем Доказательство. 1. Пусть f(x) возрастает на [ab]. Тогда при
Замечание 1. Аналогичную теорему можно доказать и для убывающей функции: Если f(x) убывает на [ab], то Замечание 2. Геометрический смысл доказанной теоремы: если функция возрастает на отрезке [ab], то касательная к ее графику во всех точках на этом отрезке образует с осью Ох острый угол (или горизонтальна). Если же функция убывает на рассматриваемом отрезке, то касательная к графику этой функции образует с осью Ох тупой угол (или в некоторых точках параллельна оси Ох). Необходимое условие экстремума. В лекции 19 было дано определение максимума и минимума функции. Теорема 22.2 (необходимое условие экстремума). Пусть функция f(x) задана в некоторой окрестности точки х0. Если х0 является точкой экстремума функции, то Доказательство. Действительно, производная в точке х0 либо существует, либо нет. Если она существует, то по теореме Ферма она равна нулю. Примеры.
Замечание. Отметим еще раз, что теорема 22.2 дает необходимое, но не достаточное условие экстремума, то есть не во всех точках, в которых f ′(x) = 0, функция достигает экстремума. Пример. У функции y = x³ y ′ = 3x2 = 0 при х = 0, однако функция монотонно возрастает во всей области определения. Определение 22.2. Если функция определена в некоторой окрестности точки х0 и ее производная в этой точке равна нулю или не существует, точка х0 называется критической точкойфункции. Теорема 22.1 означает, что все точки экстремума находятся в множестве критических точек функции. Достаточные условия экстремума. Теорема 22.3. Пусть функция f(x) непрерывна в некоторой окрестности точки х0, дифференцируема в проколотой окрестности этой точки и с каждой стороны от данной точки f ′(x) сохраняет постоянный знак. Тогда: 1) если f ′(x) > 0 при x < x0 и f ′(x) < 0 при x > x0 , точка х0 является точкой максимума; 2) если f ′(x) < 0 при x < x0 и f ′(x) > 0 при x > x0 , точка х0 является точкой минимума; 3) если f ′(x) не меняет знак в точке х0 , эта точка не является точкой экстремума. Доказательство. Справедливость утверждения 3) следует из теоремы 22.1. Докажем утверждения 1) и 2). По формуле Лагранжа f(x) – f(x0) = f ′(ξ)(x – x0), где х принадлежит окрестности точки х0, а ξ лежит между х и х0. Если f ′(ξ) > 0 при x < ξ < x0 и f ′(ξ) < 0 при х0 < ξ < x, приращение функции f(x) – f(x0) < 0 по обе стороны х0 , то есть в рассматриваемой точке достигается максимум. Если же производная при х = х0 меняет знак с «+» на «-», точка х0 является точкой минимума. Следовательно, изменение знака производной в точке х0 является необходимым и достаточным условием наличия экстремума в этой точке.
Теорема 22.4. Пусть f ′(x0) = 0 и у рассматриваемой функции существует непрерывная вторая производная в некоторой окрестности точки х0. Тогда х0 является точкой максимума, если f ′′(x0) < 0, или точкой минимума, если f ′′(x0) > 0. Доказательство. Докажем первую часть теоремы. Пусть f ′′(x0) < 0. Так как по условию f ′′(x) непрерывна, существует окрестность точки х0 , в которой f ′′(x) < 0. Вспомним, что f ′′(x) = (f ′(x))′ , и из условия (f ′(x))′ < 0 следует, что f ′(x) убывает в рассматриваемой окрестности. Поскольку f ′(x0) = 0 , f ′(x) > 0 при x < x0 и f ′(x) > 0 при x > x0. Тогда по теореме 22.3 точка х0 является точкой максимума функции, что и требовалось доказать. Утверждение 2) доказывается аналогично. Теорема 22.5. Пусть функция y = f(x) n раз дифференцируема в точке х0 и f (k)(x0) = 0 при k = 1,2,…, n-1, а f (n) (x0) ≠ 0. Тогда, если n – четное число (n = 2m), функция f(x) имеет в точке х0 экстремум, а именно максимум при f (2m)(x0) < 0 и минимум при f (2m)(x0) > 0. Если же n – нечетное число (n = 2m – 1), то точка х0 не является точкой экстремума. Доказательство. Из формулы Тейлора (21.6) следует, что а) Если n = 2m – четное и f (2m)(x0) < 0, то найдется окрестность точки х0, в которой f (2m) (x) < 0. Пусть х принадлежит этой окрестности, тогда ξ тоже ей принадлежит, то есть f (2m)(ξ) < 0. Но (x – x0)2m > 0 при х ≠ х0 , поэтому f(x) – f(x0) < 0 во всей рассматриваемой окрестности, следовательно, точка х0 является точкой максимума. б) Если n = 2m – четное и f (2m)(x0) > 0, то таким же образом доказывается, что х0 – точка минимума. в) Если n = 2m - 1 – нечетное, то (x – x0)2m-1 имеет разные знаки по разные стороны точки х0. Поэтому в окрестности этой точки, в которой производная порядка 2m – 1 сохраняет постоянный знак, приращение функции меняет знак при х = х0. Следовательно, экстремум в этой точке не достигается. Вывод: проверить наличие экстремума в критической точке можно тремя способами: 1) убедиться, что f ′(x) меняет знак при х = х0 ; 2) определить знак f ′′(x0) ; 3) если f ′′(x0) = 0, исследовать порядок и знак производной, не обращающейся в 0 в рассматриваемой точке. Примеры. 1. Определим тип экстремума функции y = x³ - 3x + 7 при х = 1. Точка х = 1 является критической, так как y′ = 3x² - 3x = 0 при х = 1. Так как при x < 1 y ′ < 0, а при x > 1 y ′ > 0, x =1 – точка минимума. Можно было установить этот факт и с помощью второй производной: y ′′ = 6x – 3 = 3 > 0 при х = 1. Следовательно, функция в этой точке достигает минимума (теорема 22.4). 2. Исследуем на экстремум функцию y = x5 + x3. y ′ = 5x4 + 3x² = x²(5x² + 3) = 0 при х = 0. При этом y′′ = 20x³ + 6x = 0 при х = 0, y′′′ = 60x² + 6 = 6 ≠ 0 при х = 0. Порядок первой ненулевой производной в точке х = 0 равен нечетному числу 3, следовательно, по теореме 22.5 функция не имеет экстремума в этой точке, а так как критическая точка единственна, функция вообще не имеет экстремумов. 12 |



 таких, что x1 < x2, f(x1) < f(x2) ( f(x1) > f(x2) ).
таких, что x1 < x2, f(x1) < f(x2) ( f(x1) > f(x2) ). на [ab].
на [ab]. для a < x < b, то эта функция возрастает на отрезке [ab].
для a < x < b, то эта функция возрастает на отрезке [ab].
 то есть
то есть  Если же
Если же 
 поэтому
поэтому  Следовательно, в обоих случаях
Следовательно, в обоих случаях  Значит,
Значит,  что и требовалось доказать.
что и требовалось доказать. Выберем
Выберем  По теореме Лагранжа
По теореме Лагранжа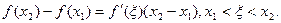 Но по условию
Но по условию  поэтому f(x2) > f(x1), следовательно, f(x) – возрастающая функция.
поэтому f(x2) > f(x1), следовательно, f(x) – возрастающая функция. на [ab]. Если
на [ab]. Если  на (ab), то f(x) убывает на [ab].
на (ab), то f(x) убывает на [ab]. или не существует.
или не существует.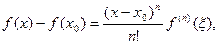 где ξ лежит между х и х0.
где ξ лежит между х и х0.