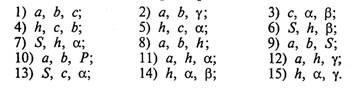ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Вычисления в математических задачах

12 3 4

Основы программирования

Задачи по теме «Линейные программы»

Задачи систематизированы по конструкциям языка, охватывают 17 тем и сгруппированы в разделы. Нумерация упражнений в каждом разделе начинается с номера один. Кроме того, предлагается набор «больших проектов», которые могут быть реализованы в конце изучения курса программирования для закрепления и развития навыков программирования.

В большинстве разделов задачи разделены по трудности на три уровня:

А — содержит простые задачи, решения которых сводятся к типовым алгоритмам;

В — содержит более сложные задачи, требующие сочетания типовых алгоритмов и определенного творческого подхода;

С — содержит задачи, рекомендованные для выполнения наиболее подготовленными учащимися.

Задачи составлены с учетом опыта проведения практических и лабораторных занятий по программированию на математическом факультете и факультете информатики и экономики Пермского государственного педагогического университета. Использованы также задачи из сборников, приведенных в списке литературы. Раздел «Задачи по теме "Модули"» содержит только авторские разработки.

Вычисления по формулам

Вычислить значение выражения по формуле (все переменные принимают действительные значения):

Вычисления в математических задачах

1. Вычислить периметр и площадь прямоугольного треугольника по длинам а и b двух катетов.

2. Заданы координаты трех вершин треугольника (x1, y1), (х2, y2), (x3, y3). Найти его периметр и площадь.

3. Вычислить длину окружности и площадь круга одного и того же заданного радиуса R.

4. Найти произведение цифр заданного четырехзначного числа.

5. Даны два числа. Найти среднее арифметическое кубов этих чисел и среднее геометрическое модулей этих чисел.

6. Вычислить расстояние между двумя точками с данными координатами (x1, y1) и (x2, y2).

7. Даны два действительных числа х и у. Вычислить их сумму, разность, произведение и частное.

8. Дана длина ребра куба. Найти площадь грани, площадь полной поверхности и объем этого куба.

9. Дана сторона равностороннего треугольника. Найти площадь этого треугольника, его высоту, радиусы вписанной и описанной окружностей.

10. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

11. Найти площадь кольца, внутренний радиус которого равен r, а внешний — R (R > r).

12. Треугольник задан величинами своих углов и радиусом описанной окружности. Найти стороны треугольника.

13. Найти площадь равнобедренной трапеции с основаниями а и b и углом α при большем основании а.

14. Вычислить корни квадратного уравнения ax² + bx + с = 0 с заданными коэффициентами а, b и с (предполагается, что а ≠ 0 и что дискриминант уравнения неотрицателен).

15. Дано действительное число х. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить за минимальное число операций

16. Дано значение х. Получить значения -2х + 3x2 - 4x3 и 1 + 2х + 3х2 + 4х3. Позаботиться об экономии операций.

17. Найти площадь треугольника, две стороны которого равны а и b, а угол между этими сторонами γ.

18. Дано значение а. Не используя никаких функций и никаких операций, кроме умножения, получить значение a8 за три операции и а10 за четыре операции.

19. Написать программу, которая выводит на экран первые четыре степени числа п.

20. Найти сумму членов арифметической прогрессии, если известны ее первый член, знаменатель и число членов прогрессии.

21. Найти (в радианах в градусах) все углы треугольника со сторонами а, b, с.

22. Составить программу перевода радианной меры угла в градусы, минуты и секунды.

23. Три сопротивления R1, R2, R3 соединены параллельно. Найдите сопротивление соединения.

24. Составить программу для вычисления пути, пройденного лодкой, если ее скорость в стоячей воде v км/ч, скорость течения реки v1 км/ч, время движения по озеру t1 ч, а против течения реки — t2 ч.

25. Текущее показание электронных часов: т ч (0 ≤ т ≤ 23) п мин (0 ≤ n ≤ 59) k с (0≤ k ≤ 59). Какое время будут показывать часы через р ч q мин r с?

26. Вычислить высоты треугольника со сторонами а, b, с.

27. Полторы кошки за полтора часа съедают полторы мышки. Сколько мышек съедят X кошек за Y часов?

28. Составить программу вычисления объема цилиндра и конуса, которые имеют одинаковую высоту Н и одинаковый радиус основания R.

29. Ввести любой символ и определить его порядковый номер, а также указать предыдущий и последующий символы.

30. Дана величина А, выражающая объем информации в байтах. Перевести А в более крупные единицы измерения информации.

31. Даны натуральные числа М и N. Вывести старшую цифру дробной части и младшую цифру целой части числа M/N.

32. Дано натуральное число Т, которое представляет длительность прошедшего времени в секундах. Вывести данное значение длительности в часах, минутах и секундах в следующей форме: НН ч ММ мин SS с.

33. Дано действительное число R вида nnn. ddd (три цифровых разряда в дробной и целой частях). Поменять местами дробную и целую части числа и вывести полученное значение числа.

34. Заданы два вектора с координатами (X1, Y1, Z1) и (Х2, Y2, Z2). Определить угол между векторами.

35. Вычислить площадь и периметр правильного N-угольника, описанного около окружности радиуса R (рассмотреть N — целого типа, R — вещественного типа).

36. Определить, во сколько раз площадь круга радиуса R больше площади сегмента, отсеченного хордой длины А.

37. Найти частное произведений четных и нечетных цифр четырехзначного числа.

38. Задан вектор с координатами (х, у, z). Найти углы наклона этого вектора к координатным осям.

39. Найти площадь круга, вписанного в треугольник с заданными сторонами.

40. Окружность вписана в квадрат заданной площади. Найти площадь квадрата, вписанного в эту окружность. Во сколько раз площадь вписанного квадрата меньше площади заданного?

41. Представить комплексное число А + Bi (А, В — вещественные) в тригонометрическом виде.

42. Треугольник задан величинами своих углов и радиусом вписанной окружности. Найти стороны треугольника.

43. Дан прямоугольный треугольник ABC (γ = 90°), для которого определен следующий набор характерных параметров (рис. 53): а, b, с — стороны треугольника; α, β — острые углы (в градусах); h — высота, опущенная на гипотенузу с; S — площадь; Р — периметр треугольника. По двум заданным параметрам вычислить все остальные. Возможные сочетания данных параметров:

44. Дан произвольный треугольник ABC (рис. 54), для которого определен следующий набор характерных параметров: а, b, с — стороны треугольника; α, β, γ — углы (в градусах); h — высота, опущенная на сторону с; S — площадь; Р — периметр треугольника. По трем заданным параметрам вычислить все остальные. Возможные сочетания параметров:

12 3 4