 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Рівносильність та тотожність формул 12
На відміну від табличного задання реалізація функції формулою не єдина. Наприклад, якщо множина логічних зв’язок  і і  позначається позначається  . . Теорема (про основні рівносильності формул). Для будь-яких формул
Доведення (самостійно) всіх рівносильностей проводиться шляхом складання таблиць істинності для формул, що стоять в лівій і правій частинах. Доведемо, наприклад, рівносильність 5 – закон де Моргана.
Оскільки формули в лівій і правій частинах набувають однакових значень при будь-яких значеннях змінних, які входять в них, то вони рівносильні. Стандартний метод доведення еквівалентності двох формул, який завжди приводить до відповіді, полягає в переході від формул до таблиць і порівнянні отриманих таблиць. Цей метод потребує 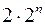 обчислень и на практиці виявляється дуже громіздким.Іншим методом доведення еквівалентності двох формул є метод рівносильних перетворень формул булевих функцій. Очевидно, що заміна в формулі деякої підформули на рівносильну дає формулу, рівносильну початковій. На основі цього можна здійснювати рівносильні перетворення формул, які не змінюють функцій, що реалізуються. обчислень и на практиці виявляється дуже громіздким.Іншим методом доведення еквівалентності двох формул є метод рівносильних перетворень формул булевих функцій. Очевидно, що заміна в формулі деякої підформули на рівносильну дає формулу, рівносильну початковій. На основі цього можна здійснювати рівносильні перетворення формул, які не змінюють функцій, що реалізуються. Означення.Рівносильним перетворенням даної формули називається заміна формули іншою формулою, їй рівносильною. Приклад. Довести рівносильність формул а) за допомогою таблиць; б) шляхом рівносильних перетворень. Розв’язання. а)
б)
Означення. Спрощенням формули називається рівносильне перетворення, яке приводить до формули, що містить лише символи
Наступні важливі рівносильності показують, як одні елементарні булеві функції можуть бути виражені через інші, наприклад: 1) 2) 3) 4)
Множина
Цей ізоморфізм показує тісний зв'язок між булевими функціями і множинами. Булеві функції визначають операції над двома множинами – універсальною і порожньою. Тому всі правила і закони теорії множин мають місце і для булевих функцій.
Принцип двоїстості Звернемо увагу на характер відповідностей між рівносильностями, які наведені в теоремі про основні рівносильності формул під номерами № і №*. Ці рівносильності такі, що одна може бути отримана з іншої заміною символу операції Означення. Логічні зв’язки Означення. Нехай формула Теорема (про двоїсту функцію).
Приклад. Побудувати формулу, двоїсту формулі а) за означенням; б) за теоремою про двоїсту формулу. Розв’язання. а) Для побудовифункції, двоїстої до функції
Тепер замінимо символи
б)
Теорема (про двоїстість). Якщо формули Зауваження. В означенні формули символи 0 і 1 також вважаються формулами. При переході до двоїстої формули 0 замінюється 1, а 1 – 0. Наприклад, Справедливий принцип двоїстості: Якщо є деяке означення або твердження, яке містить тільки символи Принцип двоїстості можна використовувати для знаходження нових рівносильностей. Наприклад, для першого закону поглинання (рівносильність 4) 12 |



 утворена функціями
утворена функціями  , то функцію | – "штрих Шеффера" – можна у відповідності із законами де Моргана реалізувати як
, то функцію | – "штрих Шеффера" – можна у відповідності із законами де Моргана реалізувати як  або
або  , а функцію "стрілка Пірса" як
, а функцію "стрілка Пірса" як  або
або  .
. справедливі рівносильності:
справедливі рівносильності:


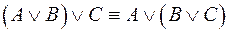
 відносно
відносно  3. А&(ВÚС)º(А&В)Ú(А&С)
3. А&(ВÚС)º(А&В)Ú(А&С)






 ;
; 
 ;
; 


 ,
, 















 .
. , причому знак
, причому знак  ; 5)
; 5)  ;
; ; 6)
; 6)  ;
; ; 7)
; 7) 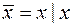 ;
; ; 8)
; 8)  .
. разом з кон’юнкцією, диз’юнкцією і запереченням утворює булеву алгебру
разом з кон’юнкцією, диз’юнкцією і запереченням утворює булеву алгебру 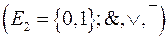 – алгебру булевих функцій. Одиницею в ній є символ 1, нулем – символ 0. Оскільки за теоремою Стоуна будь-яка булева алгебра ізоморфна алгебрі підмножин множини, яка для неї підходить, то булева алгебра
– алгебру булевих функцій. Одиницею в ній є символ 1, нулем – символ 0. Оскільки за теоремою Стоуна будь-яка булева алгебра ізоморфна алгебрі підмножин множини, яка для неї підходить, то булева алгебра  :
: .
. називається двоїстою до формули
називається двоїстою до формули  .
.
 , приведемо дану функцію за допомогою рівносильних перетворень до формули, яка містить лише символи
, приведемо дану функцію за допомогою рівносильних перетворень до формули, яка містить лише символи 
 .
.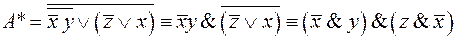 .
. , а
, а  .
.