 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Способи задання булевих функцій 12
Лекція № 5 Тема: Булеві функції
План лекції:
1. Поняття булевої функції. 2. Способи задання булевих функцій. 3. Число булевих функцій 4. Елементарні булеві функції. 5. Реалізація булевих функцій формулами. 6. Рівносильність та тотожність формул. 7. Принцип двоїстості. Поняття булевої функції При обробці дискретної інформації найчастіше використовують дискретні пристрої, в яких вхідні та вихідні сигнали мають два різних рівні. Це пов’язано з необхідністю простоти фізичної реалізації пристроїв, з необхідністю економічності і надійності виконання логічних і арифметичних операцій. Одному з рівнів присвоюється символ 0, іншому – 1 і, таким чином, пристрій здійснює обробку двійкової інформації. В зв’язку з цим природно розглянути функції, які визначені на двоелементній множині Булеві функції застосовуються в обчислювальній техніці для опису пристроїв переробки дискретної інформації, яка розкладається на елементарні одиниці – біти, які в цих пристроях реалізуються сигналами, що описуються двійковими змінними – булевими змінними. Булеві функції належать до класу двозначних однорідних функцій (однорідною називається функція, яка для будь-яких Нехай задана множина Означення. Булевою функцією називається функція Таким чином, областю визначення булевої функції є множина впорядкованих наборів з
Оскільки множина Позначимо набір значень змінних  , , 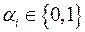 , ,  , значень для , значень для  аргументів аргументів  булевої функції дорівнює булевої функції дорівнює  .Приклад. Для функції .Приклад. Для функції 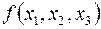 можна задати можна задати 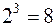 різних двійкових наборів значень аргументів різних двійкових наборів значень аргументів  : :
 двійкових наборів функції є байдужими, то часткову функцію можна довизначити двійкових наборів функції є байдужими, то часткову функцію можна довизначити  способами. Інакше кажучи, кожній такій частковій функції відповідає множина з способами. Інакше кажучи, кожній такій частковій функції відповідає множина з  цілком визначених булевих функцій, отриманих шляхом різних довизначень.Означення. Змінна цілком визначених булевих функцій, отриманих шляхом різних довизначень.Означення. Змінна  , яка є аргументом булевої функції , яка є аргументом булевої функції  , називається неістотною (фіктивною), якщо , називається неістотною (фіктивною), якщо  = =  при будь-яких значеннях інших змінних, тобто якщо зміна значення при будь-яких значеннях інших змінних, тобто якщо зміна значення  в будь-якому наборі значень змінних в будь-якому наборі значень змінних  не змінює значення функції. В цьому випадку функція не змінює значення функції. В цьому випадку функція  істотно залежить від істотно залежить від  змінної, тобто являє собою функцію змінної, тобто являє собою функцію 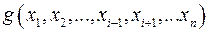 від від  змінної.Кажуть, що функція змінної.Кажуть, що функція  отримана з функції отримана з функції  видаленням фіктивної змінної, а функція видаленням фіктивної змінної, а функція  отримана з функції отримана з функції  введенням фіктивної змінної, причому ці функції вважаються рівними.Приклад. введенням фіктивної змінної, причому ці функції вважаються рівними.Приклад.  означає, що при будь-яких значеннях означає, що при будь-яких значеннях   незалежно від значень незалежно від значень  . Змінна . Змінна  – фіктивна.Означення. Константою 0 (константою 1) називається цілком визначена булева функція, яка на всіх наборах дорівнює 0 (1), тобто функція з – фіктивна.Означення. Константою 0 (константою 1) називається цілком визначена булева функція, яка на всіх наборах дорівнює 0 (1), тобто функція з  неістотними змінними. неістотними змінними.
Способи задання булевих функцій Прийнято наступні способи завдання булевих функцій: 1. Табличний спосіб. З означення випливає, що для задання булевої функції достатньо вказати, які значення функції відповідають кожному з наборів значень аргументів, тобто скласти таблицю значень функції. Таблиця значень булевої функції називається таблицею істинності булевої функції. Таблиця істинності – таблиця, в якій кожному двійковому набору значень змінних ставиться у відповідність значення функції ставиться у відповідність значення функції  на даному наборі або прочерк, якщо значення функції на даному наборі або прочерк, якщо значення функції  на даному наборі не визначено. В останньому випадку байдужий набір в таблицю можна не включати. на даному наборі не визначено. В останньому випадку байдужий набір в таблицю можна не включати.
 -розрядне ціле двійкове число. В силу цього рядки в таблиці істинності зручно розташовувати в природному порядку зростання двійкових чисел -розрядне ціле двійкове число. В силу цього рядки в таблиці істинності зручно розташовувати в природному порядку зростання двійкових чисел 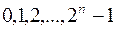 , а десятковий еквівалент даного числа вважати номером відповідного двійкового набору.Приклад. Нехай , а десятковий еквівалент даного числа вважати номером відповідного двійкового набору.Приклад. Нехай  =3. Розглянемо довільну функцію трьох змінних =3. Розглянемо довільну функцію трьох змінних
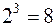 , функції відповідає двійковий вектор значень довжини , функції відповідає двійковий вектор значень довжини 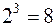 . Звідки випливає ще один спосіб задання булевої функції:2. Векторний спосіб – коли булева функція подається у вигляді вектора своїх значень . Звідки випливає ще один спосіб задання булевої функції:2. Векторний спосіб – коли булева функція подається у вигляді вектора своїх значень  , ,  , ,  . Координата . Координата  є значенням функції є значенням функції  на наборі значень змінних на наборі значень змінних  з номером з номером  , ,  .Приклад. Булева функція з попереднього прикладу може бути подана у вигляді вектора: .Приклад. Булева функція з попереднього прикладу може бути подана у вигляді вектора:  .Розглядаючи двійковий вектор як двійкове ціле число з .Розглядаючи двійковий вектор як двійкове ціле число з  розрядами, будемо вважати десятковий еквівалент цього двійкового числа номером (індексом) функції, яка задана даною таблицею. В нашому випадку задана функція розрядами, будемо вважати десятковий еквівалент цього двійкового числа номером (індексом) функції, яка задана даною таблицею. В нашому випадку задана функція  .Позначимо через .Позначимо через  множину всіх двійкових наборів, на яких булева функція множину всіх двійкових наборів, на яких булева функція  набуває значення 1, тобто набуває значення 1, тобто  . Будемо називати двійковий набір, на якому булева функція . Будемо називати двійковий набір, на якому булева функція  набуває значення 1, одиничним вектором. Тоді множина набуває значення 1, одиничним вектором. Тоді множина  називається множиною одиничних векторів або просто одиничною множиною функції називається множиною одиничних векторів або просто одиничною множиною функції  . Звідси випливає ще один спосіб задання булевої функції: . Звідси випливає ще один спосіб задання булевої функції: 3. Геометричний спосіб – коли булева функція задається своєю одиничною множиною Суто геометрична інтерпретація ефективна для невеликого числа змінних. При
При
При
Щоб задати булеву функцію, вказують не самі одиничні вектори, а їх номери. Таким чином, булева функція Приклад. Одинична множина булевої функції
На виділених векторах функція набуває значення 1. Існують ще два способи задання булевих функцій – формулами і схемами з функціональних елементів, з якими познайомимося пізніше.
3. Число булевих функцій  множину всіх можливих булевих функцій від множину всіх можливих булевих функцій від  змінних, включаючи функції з фіктивними змінними. Визначимо потужність множини змінних, включаючи функції з фіктивними змінними. Визначимо потужність множини  . Якщо зафіксувати один з аргументів булевої функції . Якщо зафіксувати один з аргументів булевої функції  , надаючи йому конкретне стале значення з множини , надаючи йому конкретне стале значення з множини  , то отримаємо булеву функцію від , то отримаємо булеву функцію від  –го аргументу. Так, фіксуючи –го аргументу. Так, фіксуючи  , ,  , можна отримати дві нові булеві функції від , можна отримати дві нові булеві функції від  –го аргументу: –го аргументу:  і і  , які будуть задаватися таблицями, що відрізняються тільки значеннями правих стовпців. Якщо зафіксувати всі , які будуть задаватися таблицями, що відрізняються тільки значеннями правих стовпців. Якщо зафіксувати всі  змінних змінних  , то різні таблиці, що задають булеві функції, будуть відрізнятися тільки значеннями правого стовпця. Тому справедлива теоремаТеорема (про число булевих функцій від , то різні таблиці, що задають булеві функції, будуть відрізнятися тільки значеннями правого стовпця. Тому справедлива теоремаТеорема (про число булевих функцій від  аргументів). Число різних булевих функцій від аргументів). Число різних булевих функцій від  аргументів дорівнює аргументів дорівнює  : :  .Доведення. Для задання булевої функції .Доведення. Для задання булевої функції  від від  аргументів треба вказати її значення для кожного з аргументів треба вказати її значення для кожного з  різних наборів значень її аргументів, тобто заповнити правий стовпець таблиці істинності функції. Оскільки порядок рядків в таблиці однаковий, то різних булевих функцій від різних наборів значень її аргументів, тобто заповнити правий стовпець таблиці істинності функції. Оскільки порядок рядків в таблиці однаковий, то різних булевих функцій від  аргументів існує стільки, скільки можна скласти різних правих стовпців. А оскільки кожний стовпець являє собою двійковий набір довжини аргументів існує стільки, скільки можна скласти різних правих стовпців. А оскільки кожний стовпець являє собою двійковий набір довжини  , то кількість таких наборів за лемою дорівнює , то кількість таких наборів за лемою дорівнює  .□Відзначимо, що із зростанням .□Відзначимо, що із зростанням  число різних булевих функцій від число різних булевих функцій від  аргументів швидко зростає: при аргументів швидко зростає: при  їх 4, при їх 4, при  їх 16, при їх 16, при  – 256, при – 256, при  – 655536 і т.д. Із зростанням числа аргументів, таблиця, що задає булеву функцію, дуже ускладнюється; вже при – 655536 і т.д. Із зростанням числа аргументів, таблиця, що задає булеву функцію, дуже ускладнюється; вже при  таблиця стає величезною (1024 рядки), а при таблиця стає величезною (1024 рядки), а при  – практично неосяжною. Тому при великих – практично неосяжною. Тому при великих  табличний спосіб завдання булевих функцій незастосовний. табличний спосіб завдання булевих функцій незастосовний. 12 |



 і набувають значень в ній ж. Такі функції називаються булевими функціями (інші назви: функції алгебри логіки, двійкові функції, перемикальні функції). Булеві функції отримали свою назву від прізвища англійського математика Джорджа Буля (1815–1864), який першим застосував математичні методи до логіки.
і набувають значень в ній ж. Такі функції називаються булевими функціями (інші назви: функції алгебри логіки, двійкові функції, перемикальні функції). Булеві функції отримали свою назву від прізвища англійського математика Джорджа Буля (1815–1864), який першим застосував математичні методи до логіки. і будь-яких скалярів
і будь-яких скалярів  таких, що
таких, що  ).
). . Зазначимо, що елементи множини
. Зазначимо, що елементи множини  0 і 1 не є числами в звичайному розумінні, це – формальні символи. Найбільш розповсюджена їх інтерпретація – логічна: "ні" – "так", " хибне " – "істинне".
0 і 1 не є числами в звичайному розумінні, це – формальні символи. Найбільш розповсюджена їх інтерпретація – логічна: "ні" – "так", " хибне " – "істинне".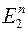 , а множиною значень є множина
, а множиною значень є множина  ,
,  . Отже,
. Отже, .
.





 ,
, 




 область визначення булевої функції трьох змінних – множина вершин 3-вимірного одиничного куба.
область визначення булевої функції трьох змінних – множина вершин 3-вимірного одиничного куба.
 – вказані номери одиничних векторів, тобто функція задається переліком десяткових еквівалентів наборів, на яких вона дорівнює одиниці.
– вказані номери одиничних векторів, тобто функція задається переліком десяткових еквівалентів наборів, на яких вона дорівнює одиниці.